利用位置活动基元(LAMs)挖掘工作日与周末的联系
📑 原始论文:Revealing correlation patterns of individual location activity motifs between workdays and day-offs using massive mobile phone data
摘要
利用海量手机数据揭示工作日和休息日间个体位置活动基元的关联模式
近年来,人们对理解更广泛、更长期的跨日甚至跨周的个体活动-出行行为(individual daily activity-travel behaviors)越来越感兴趣。然而,个体在多天中的日常活动-出行行为之间的关系仅部分被揭示,尤其是在工作日和休息日之间。
因此,我们开发了一个有效的框架,从海量的手机网络数据中提取基于位置活动基元 ( Location Activity Motifs,LAMs ) 的个体日常活动-出行模式,这有利于将日常活动-出行行为中的位置、活动和出行结合起来。
研究发现,在排除出行次数的影响后,LAMs随时间变化的数量很好地符合经典的探索和偏好返回 ( exploration and preferential return,EPR ) 模型,再现了日尺度上的人类活动-出行行为特征,表明工作日和休息日之间存在着复杂的 LAMs 关系。
此外,我们给出了三类关联模式,并使用关联规则挖掘算法实例化了工作日和休息日LAM之间的关系。
最终,规律性的个体差异和明显的空间异质性揭示了关联模式的形成机制。这些实证结果有助于在工作日和非工作日之间制定不同但相关的运输策略。
论文标题
Revealing correlation patterns #4 of individual location activity motifs#2 between workdays and day-offs#3 using massive#1 mobile phone data
重读论文标题,我们抓住了以上几个关键词,而这篇论文也正好是按照这样的顺序进行编排的。
本文的目的是为了挖掘【关联模式】,这个关联模式是【基元】之间的,而基元是【日尺度(multi-days scale)】的,用于表征日常活动-出行的行为,所用的数据是【海量】的手机。
接下来我们将从这四个点逐步展开对这篇论文的解读。
Massive|语义锚点检测
已有的研究中不乏有尝试从海量位置感知数据中提取个体活动-出行指标的方法:
- 跳转长度(Jump Length)
- 均方位移(Mean Square Displacement)
- 回转半径(Radius of Gyration)
- 最频繁位置(most Frequent Location)
但这些指标普遍没有考虑到轨迹点的有效性:一个有效的踪迹点应该是一个人主动选择执行有价值的活动的地点,例如居住,工作,购物,餐饮等,而不是一个偶然的地点。
为了提取个体活动-出行指标,我们应该通过创建更有语义点来进行后续处理。所以作者采用了语义锚点检测(Semantic anchor points detection)方法。
推导位置锚点
假设每个时刻只有一个用户连接到一个手机塔,但信号强度的交换会导致用户在手机塔之间的信令位置发生偏移。为了获取确切位置,我们可以定义位置点为:
- 信令位置在距离阈值 内;
- 持续时间超过阈值 ;
- 计算加权中心;
- 将加权中心位置放置到预先划分的250m 网格中;
- 将网格中坐落的位置定义为锚点的最终位置。
这减少了由于信号波动或其他原因可能造成的定位误差。
活动语义锚点
我们可以通过一些先验知识为每个锚点分配一个活动目的:家(Home),工作(Work) 以及其他(Others)。例如:
| 语义锚点 | 判断依据 |
|---|---|
| Work | 9:00 AM - 5:00 PM (工作日) |
| Home | 9:00 PM - 8:00 AM |
| Others | …… |
Motifs|位置活动基元
在确定锚点后,利用锚点的位置我们可以构建以一天为基本时间单位的个体日常出行轨迹。结合锚点的活动语义,这个个体出行轨迹自然也是含有语义信息的。
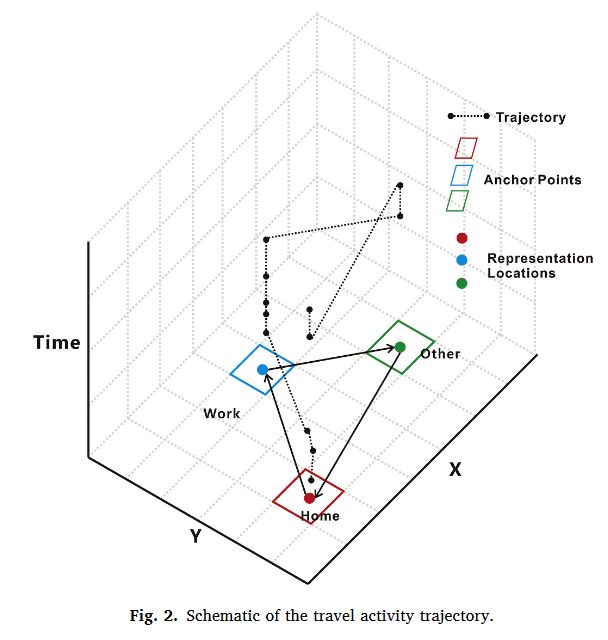
这个轨迹可以抽象成一个简单的活动模体,也可以说是人类行为活动的一种基元。
与传统的基于活动的模体相比,上面构建的位置活动基元 LAMs 能够有效地区分活动的位置差异。传统的活动移动基元(Mobility motifs, MMs)中, H-O-W-O-H 这样的网络基元不能确定其他 O 是否是同一个 O ,但可以在LAMs中识别。
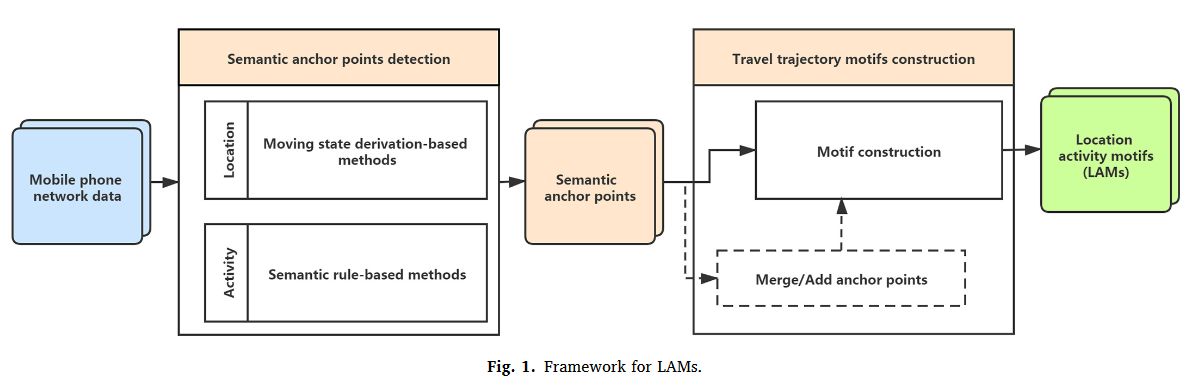
Multi-days|拟合经典模型
经典个体层次的移动模型,有:
- Levy flight 模型 (Brockmann, Hufnagel, & Geisel, 2006);
- 连续时间随机游走(CTRW)模型 (Gonz ’ alez et al. , 2008);
- 探索与偏好返回(EPR)模型 (Song et al. , 2010)
主要描述了个体活动-出行行为的空间选择机制,反应了每天回到一个或多个地点的倾向。
但在揭示日尺度上的活动形成机制方面存在一定的局限性。
而这个问题通过【Massive】的数据,和对每日构建的【LAMs】得到解决。
可以通过评估日常活动-出行模式是否符合经典的个体层次移动模型,来揭示多天中个体日常活动-出行模式的关系。
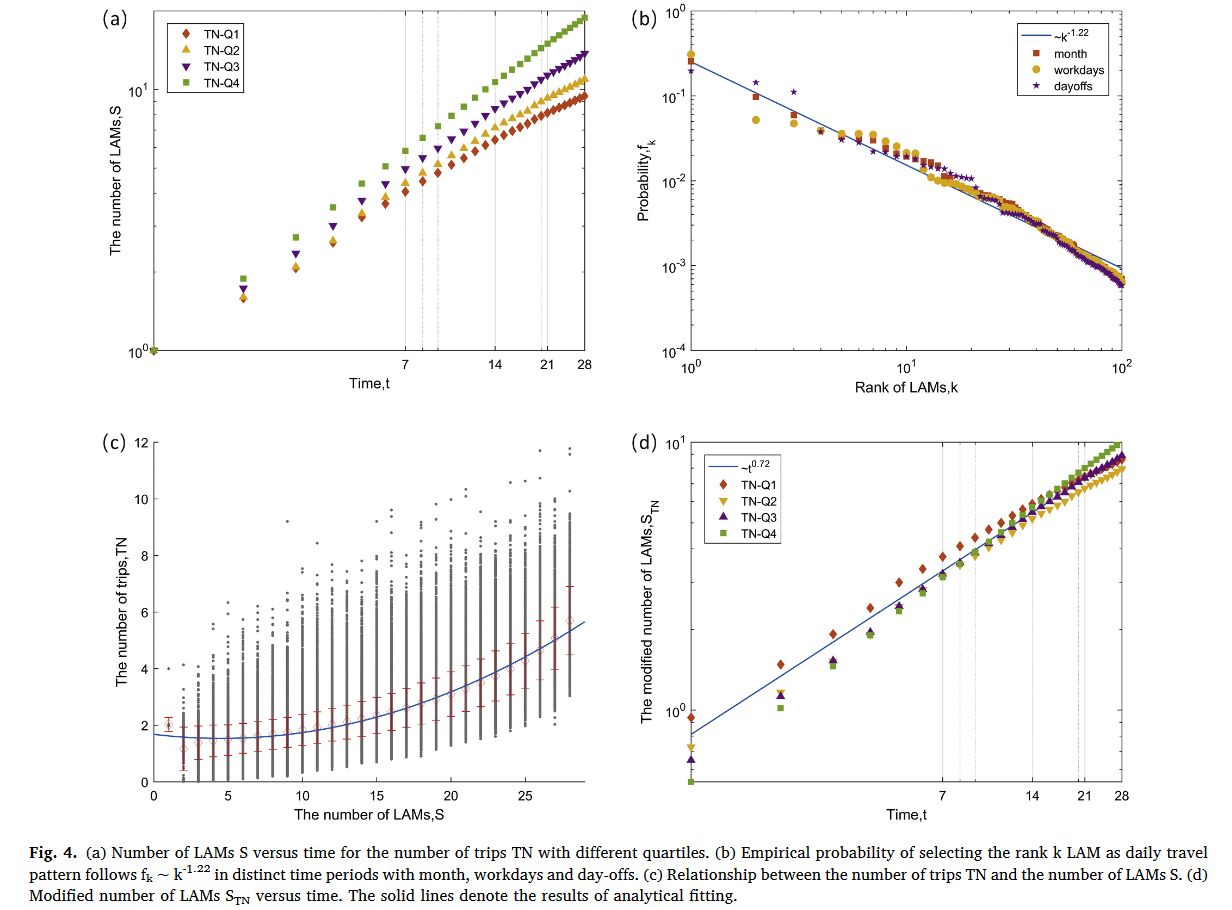
如图a所示,个体的出行次数 在四种分位下,LAM 的数量 都随着时间的增加而增加,并且 越大 也越大。
通过绘制频次图(b),可以看出,LAMs的种类频次服从齐普夫分布,这与传统模型是一致的。
此外,如图c所示,直接绘制 和 的关系图后发现, 呈 增长。因此我们可以利用 来对 进行修正:,从而使得(图d)。
Note
- :Levy flight 模型;
- : CTRW 模型;
- : EPR 模型.
可以看出 LAMs 的数量(修正后)与时间的关系与 EPR模型 相符。为了进一步确认是否符合EPR模型,我们继续探究了 与 之间的关系。
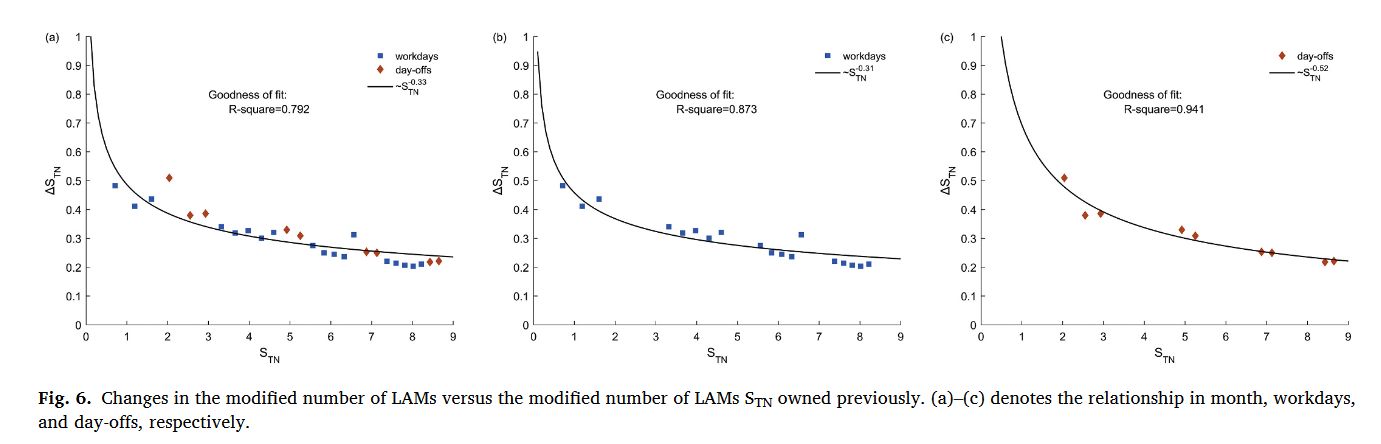
这也符合 EPR模型中个体移动到先前未访问过的位置的概率 的条件。
并且发现,当工作日与周末分开拟合时,效果更好! 这间接体现了不同性质的日之间的独立性。
Correlation Patterns|关联模式
研究者利用关联规则算法探究工作日与非工作日之间LAM的关联模式。
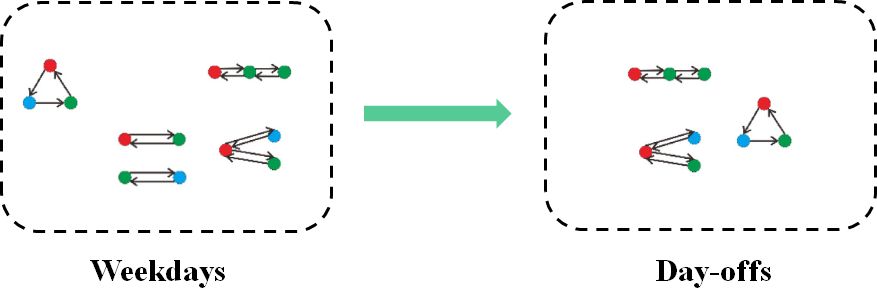
具体步骤如下:
- 数据预处理。在LAMs的基础上,提取工作日和休息日的个体LAM。然后,定义特定的 级关联模式,它由工作日的任意 种LAM和休息日的任意 种LAM组成。
- 在 中确定有效候选。根据 Apriori 的两条规则:如果 是有效的候选模式,它必须保证 下面这个公式 中的所有子模式都是显著频繁模式。 中的有效候选者可以从工作日的 级频繁关联模式和休息日的 级频繁关联模式中初步生成,然后通过 和 级频繁关联模式进行筛选。
其中是的子集,表示由 种工作日LAM和 种休息日LAM组成的 级关联模式。 表示在工作日从 种LAM中随机选择的 种LAM, 表示从 种LAM中随机选择的 种LAM。 表示级联算子。
- 确定 中的显著频繁模式。对于 中的每个有效候选,使用支持度和置信度两个标准来判断是否具有显著频繁。表达式如下:
式中, 为 的个体数, 为 (即 或)的个体数, 为总个体数。
多元Logistic回归模型
利用多元Logistic回归模型探索关联模式与个体特征(包括年龄、性别、收入、受教育程度、生活习惯、通勤距离、通勤时间等)的关系。
其中 表示解释关联模式 的概率, 表示基准关联模式的概率; 表示自变量,即个体特征, 为特征编号; 表示截距; 为回归系数。
缺陷
- 更多小但确切的数据期待使用进去
- 排除了游客和无业人员,因为他们的活动-旅行模式在工作日和休息日之间是不稳定的,但他们的活动也显著影响了城市环境
- 没有考虑出行方式的因素




