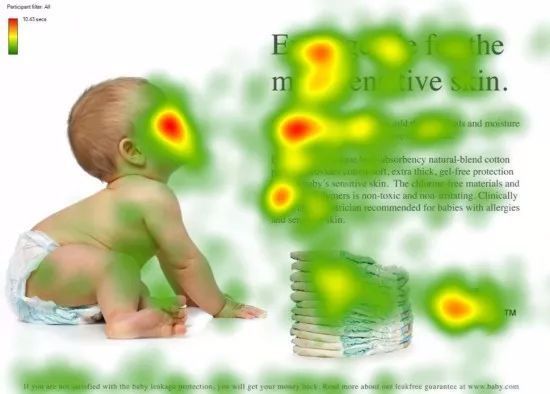
注意力机制范式 生物学注意力 灵长类动物的视觉系统接受了大量的感官输入, 这些感官输入远远超过了大脑能够完全处理的程度。 然而,并非所有刺激的影响都是相等的。将注意力引向感兴趣的物体 ,例如猎物和天敌。 只关注一小部分信息 的能力对进化更加有意义,使人类得以生存和成功。
深度学习中的 注意力机制(Attention Mechanism) 就是一种模仿人类视觉和认知系统的方法,它允许神经网络在处理输入数据时集中注意力于相关的部分。通过引入注意力机制,神经网络能够自动地学习并选择性地关注输入中的重要信息,提高模型的性能和泛化能力。
自主性提示 “美国心理学之父”,威廉·詹姆斯,对人类的这种注意力机制提出了双组件框架:受试者基于 非自主性提示 和 自主性提示 有选择地引导注意力的焦点。
非自主性提示:万花丛中一点红——我们更容易关注到花园中与其他白花有明显不同的红花。 自主性提示:受到了认知和意识的控制,自主关注某个东西。如看球赛时我们有意识地关注正在踢球的球员。 那么如何通过这两种提示, 用神经网络来设计注意力机制的框架呢?
考虑一个简单情况: 只使用“非自主性提示 ”。 此时可以简单地使用参数化的全连接层, 甚至是非参数化的最大池化层或平均池化层,这样就能把数据通过“非自主提示的注意力”得到输出。说人话就是能直接按照某种规则直接拿出一组数据中比较突出的部分。
接下来我们引入“自主性提示”,将注意力机制与池化层区分开来。
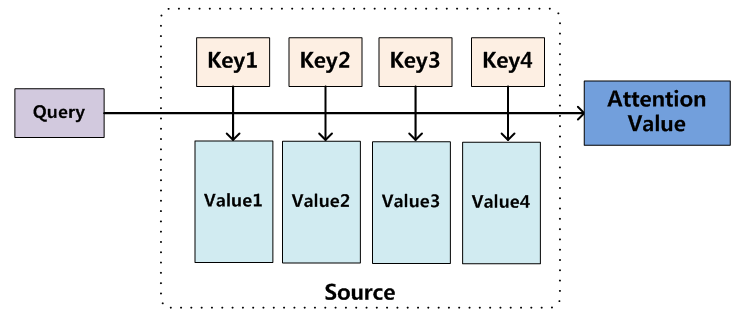
原论文最初是把注意力机制以数据库查找问题的视角来进行描述的。keys 和它通过“非自主性提示”得到的对应的 values ,把这些 k-v pairs 统称为 Source 。而所谓的“自主性提示”就是输入一个想要自主查询的目标(query ),系统可以自主地选择出最需要注意 到的 key —— 最接近 query 的 key,然后返回与 query 对应的 attention value,这就是注意力机制的核心。我们接下来就是需要考虑如何设计这种机制。
机制设计剧透(一句话版):所谓最接近就是求相似度,所谓对应的 attention value 就是加权平均所有 value。
机制的设计渊源 统计学习/机器学习领域中有这样一种处理回归问题的方法,被称作 Nadaraya-Watson核回归 。它通过引入核函数 的思想实现了非参数统计 ,利用样本距离的占比作为权重,然后对样本输出进行加权平均,进而得到整个样本的拟合函数 :
f ( x ) = ∑ i = 1 n K ( x − x i ) ∑ j = 1 n K ( x − x j ) y i , f(x) = \sum_{i=1}^n \frac{\mathcal K(x - x_i)}{\sum_{j=1}^n \mathcal K(x - x_j)} y_i, f ( x ) = i = 1 ∑ n ∑ j = 1 n K ( x − x j ) K ( x − x i ) y i ,
式中,K ( ⋅ ) {\cal K}(·) K ( ⋅ )
受此启发,注意力机制的输出(attention value)也规定是由 source 中所有的 values 的加权 平均值给出的,而这个权值由某种相似性度量函数sim ( ⋅ ) \text{sim}(·) sim ( ⋅ )
Attention ( Q u e r y , S o u r c e ) = ∑ i = 1 n sim ( Q u e r y , K e y i ) ⋅ V a l u e i \text{Attention}(Query,Source)=\sum_{i=1}^n\text{sim}(Query,Key_i)·Value_i Attention ( Q u ery , S o u rce ) = i = 1 ∑ n sim ( Q u ery , Ke y i ) ⋅ Va l u e i
更进一步地,参考Nadaraya-Watson核回归的设计思路,如果我们将核函数取为高斯函数 ,就有:
f ( x ) = ∑ i = 1 n exp ( − 1 2 ( x − x i ) 2 ) ∑ j = 1 n exp ( − 1 2 ( x − x j ) 2 ) y i = ∑ i = 1 n s o f t m a x ( − 1 2 ( x − x i ) 2 ) y i \begin{split}\begin{aligned} f(x) &= \sum_{i=1}^n \frac{\exp\left(-\frac{1}{2}(x - x_i)^2\right)}{\sum_{j=1}^n \exp\left(-\frac{1}{2}(x - x_j)^2\right)} y_i \\&= \sum_{i=1}^n \mathrm{softmax}\left(-\frac{1}{2}(x - x_i)^2\right) y_i\end{aligned}\end{split} f ( x ) = i = 1 ∑ n ∑ j = 1 n exp ( − 2 1 ( x − x j ) 2 ) exp ( − 2 1 ( x − x i ) 2 ) y i = i = 1 ∑ n softmax ( − 2 1 ( x − x i ) 2 ) y i
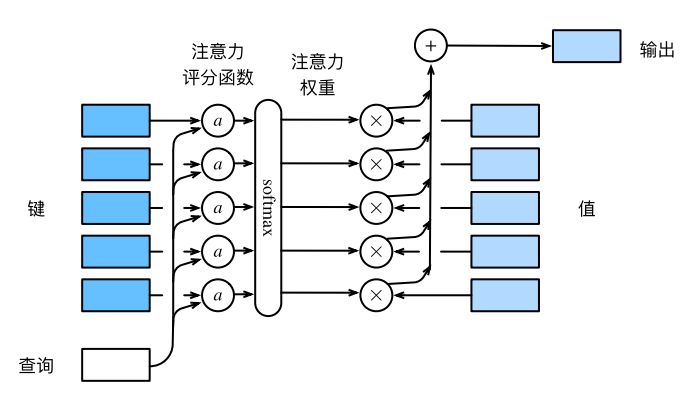
我们把s o f t m a x \mathrm{softmax} softmax 注意力评分函数 (attention scoring function),简称评分函数(scoring function),记为a ( ⋅ ) a(·) a ( ⋅ )
则上述过程可以看作对K e y s Keys Keys Q u e r y Query Q u ery a a a s o f t m a x \mathrm{softmax} softmax 归一化 。因为s o f t m a x \mathrm{softmax} softmax V a l u e Value Va l u e
整个过程如下图所示:
最终,当我们设计不同的注意力机制时,其实我们可以只需要设计不同的评分函数 。不难发现,Nadaraya-Watson核回归中的评分函数是由L 2 L_2 L 2 余弦距离 或其他相似性 。
注意力评分函数 在上一节中,我们已经指出注意力机制的本质,也就是最原始版本的注意力(vanilla attention )。我们可以灵活的改变评分函数来应对不同的问题。下面总结出一些常见情况/输入数据下评分函数可供选取。
加性注意力 当 query 和 key 是不同长度 的向量时,可以使用加性注意力作为评分函数。
a ( q , k ) = w v ⊤ tanh ( W q q + W k k ) ∈ R a(\mathbf q, \mathbf k) = \mathbf w_v^\top \text{tanh}(\mathbf W_q\mathbf q + \mathbf W_k \mathbf k) \in \mathbb{R} a ( q , k ) = w v ⊤ tanh ( W q q + W k k ) ∈ R
该过程可以看作是将查询q \bf q q k \bf k k 连结 之后,通过带有权重参数的多层感知机(禁用偏置项),然后利用t a n h \rm tanh tanh
缩放点积注意力 使用点积可以得到计算效率更高 的评分函数, 但是点积操作要求 query 和 key 具有相同的长度 d d d
假设 query 和 key 的所有元素都是独立的随机变量, 并且都满足零均值和单位方差, 那么两个向量的点积的均值为0,方差为d d d d \sqrt{d} d 缩放点积注意力 (scaled dot-product attention)评分函数为:
a ( q , k ) = q ⊤ k / d a(\mathbf q, \mathbf k) = \mathbf{q}^\top \mathbf{k} /\sqrt{d} a ( q , k ) = q ⊤ k / d
考虑小批量计算时,整个注意力机制的输出可以写成矩阵形式:
s o f t m a x ( Q K ⊤ d ) V \mathrm{softmax}\left(\frac{\mathbf Q \mathbf K^\top }{\sqrt{d}}\right) \mathbf V softmax ( d Q K ⊤ ) V
向量点积之所以能表示相似度,是因为其源头是余弦距离 (不考虑方向)
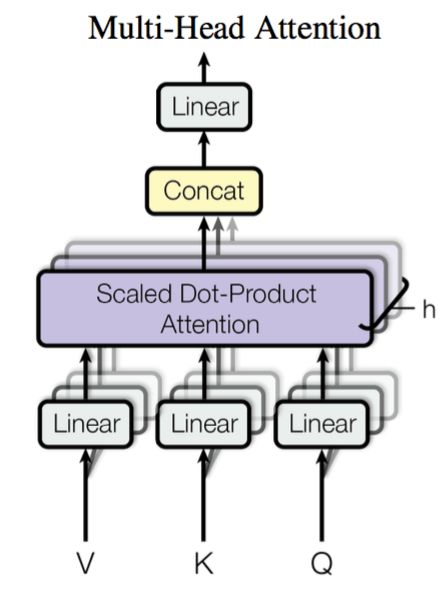
多头注意力机制 在实践中,为了捕捉不同方面的信息,将注意力机制分为多个头,形成多个子空间表示(representation subspaces)是有意义的。
用独立学习得到的h h h 线性投影 (linear projections)来变换查询、键和值。 然后将它们并行地 送到注意力池化中。 最后,将这h h h 多头注意力 (Multi-Head Attention)。
第i i i head 的查询、键和值线性变换后的结果如下:
以矩阵形式 给出,此处暂且忽略板书时对符号的加粗
Q i = Q W i Q , K i = K W i K , V i = V W i V Q_i=QW_i^Q,\;K_i=KW_i^K,\;V_i=VW_i^V Q i = Q W i Q , K i = K W i K , V i = V W i V
从而第i i i head 的输出为:
h e a d i = A t t e n t i o n ( Q i , K i , V i ) A t t e n t i o n ( Q i , K i , V i ) = s o f t m a x ( Q i K i ⊤ d ) V i \begin{aligned} \mathrm{head}_i&=\mathrm{Attention}(Q_i,K_i,V_i)\\ \mathrm{Attention}(Q_i,K_i,V_i)&=\mathrm{softmax}\left(\frac{Q_iK_i^\top }{\sqrt{d}}\right)V_i \end{aligned} head i Attention ( Q i , K i , V i ) = Attention ( Q i , K i , V i ) = softmax ( d Q i K i ⊤ ) V i
最终的多头注意力输出为:
A t t e n t i o n ( Q , K , V ) = C o n c a t ( h e a d 1 , . . , h e a d i , . . ) W O \mathrm{Attention}(Q,K,V)=\mathrm{Concat}\left(\mathrm{head}_1,..,\mathrm{head}_i,..\right)W^O Attention ( Q , K , V ) = Concat ( head 1 , .. , head i , .. ) W O
自注意力机制 自注意力机制 (self-attention)也被称为内部注意力(intra-attention),顾名思义就是对输入数据自身进行和传统注意力机制类似的处理。特别地,有q = k = v \bf q=k=v q = k = v
如果输入小批量样本X = { x 1 , . . . , x n } ∈ R n × d , x i ∈ R d {\bf X}=\{\boldsymbol x_1,...,\boldsymbol x_n\}\in\Bbb R^{n\times d},\;\boldsymbol x_i\in\Bbb R^d X = { x 1 , ... , x n } ∈ R n × d , x i ∈ R d ( x i , x i ) (\boldsymbol x_i,\boldsymbol x_i) ( x i , x i ) q = x i q=\boldsymbol x_i q = x i
y i = f ( x i , ( x 1 , x 1 ) , ( x 2 , x 2 ) , . . . , ( x n , x n ) ) ∈ R d \boldsymbol y_i=f\left(\boldsymbol x_i,\;(\boldsymbol x_1,\boldsymbol x_1),(\boldsymbol x_2,\boldsymbol x_2),...,(\boldsymbol x_n,\boldsymbol x_n)\right)\in\Bbb R^d y i = f ( x i , ( x 1 , x 1 ) , ( x 2 , x 2 ) , ... , ( x n , x n ) ) ∈ R d
其中,f f f y i \boldsymbol y_i y i 尺寸与输入一致。
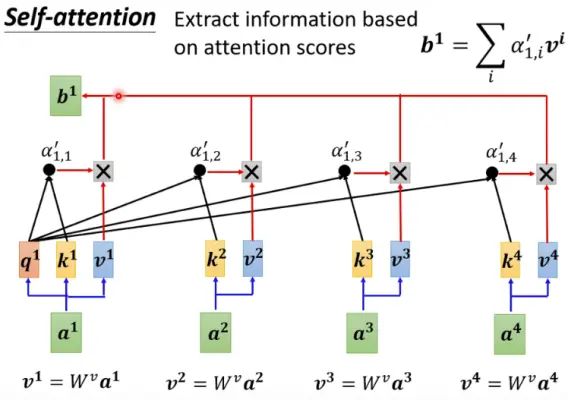
实际中的自注意力 通常情况下,我们并不是直接取q = k = v \bf q=k=v q = k = v x i \boldsymbol x_i x i q i = W q x i , k i = W k x i , v i = W v x i , i = 1 , . . , n \boldsymbol q_i=W^q\boldsymbol x_i,\;\boldsymbol k_i=W^k\boldsymbol x_i,\;\boldsymbol v_i=W^v\boldsymbol x_i,\quad i=1,..,n q i = W q x i , k i = W k x i , v i = W v x i , i = 1 , .. , n
然后再进行:
y i = f ( q i , ( k 1 , v 1 ) , ( k 2 , v 2 ) , . . . , ( k n , v n ) ) ∈ R d \boldsymbol y_i=f\left(\boldsymbol q_i,\;(\boldsymbol k_1,\boldsymbol v_1),(\boldsymbol k_2,\boldsymbol v_2),...,(\boldsymbol k_n,\boldsymbol v_n)\right)\in\Bbb R^d y i = f ( q i , ( k 1 , v 1 ) , ( k 2 , v 2 ) , ... , ( k n , v n ) ) ∈ R d
即是用q i \boldsymbol q_i q i i i i
同样地,我们可以并行地 计算出和x 1 , . . . , x n \boldsymbol x_1,...,\boldsymbol x_n x 1 , ... , x n y 1 , . . . , y n \boldsymbol y_1,...,\boldsymbol y_n y 1 , ... , y n
SelfAttention ( X ) = Attention ( X W q , X W k , X W v ) = softmax ( X W q W k ⊤ X ⊤ d k ) X W v \begin{aligned} \text{SelfAttention}(\boldsymbol{X}) =&\, \text{Attention}(\boldsymbol{X}\boldsymbol{W}_q, \boldsymbol{X}\boldsymbol{W}_k, \boldsymbol{X}\boldsymbol{W}_v)\\ =&\, \text{softmax}\left(\frac{\boldsymbol{X}\boldsymbol{W}_q \boldsymbol{W}_k^{\top}\boldsymbol{X}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{X}\boldsymbol{W}_v& \end{aligned} SelfAttention ( X ) = = Attention ( X W q , X W k , X W v ) softmax ( d k X W q W k ⊤ X ⊤ ) X W v
奠基之作 注意力机制的集大成者是如今赫赫有名的 Transformer,本文因聚焦在对于其中注意力机制的探讨,所以便略过了其在该模型中的使用。Transformer 在本站文章中有展开梳理,并回顾了由其带来的大模型热潮。
注意力数据融合 假设多源/多模态数据的种类所构成的集合为P \cal P P h p ∈ R d \mathbf{h}_p\in\mathbb R^d h p ∈ R d p ∈ P p\in \cal P p ∈ P p p p β p \beta_p β p h \bf h h
h = ∑ p ∈ P β p ⋅ h p \mathbf{h}=\sum_{p\in\cal P}\beta_p\cdot\mathbf{h}_p h = p ∈ P ∑ β p ⋅ h p
这个权值事先通过s o f t m a x \mathrm{softmax} softmax
β p = α p ∑ p ∈ P exp ( α p ) \beta_p=\frac{\alpha_p}{\sum_{p\in\cal P}\exp(\alpha_p)} β p = ∑ p ∈ P exp ( α p ) α p
而α p \alpha_p α p p p p
α p = c ⊤ ReLU ( W h p + b ) \alpha_p=\mathbf c^\top\text{ReLU}(\mathbf{Wh}_p+\mathbf b) α p = c ⊤ ReLU ( Wh p + b )
其中,c ∈ R d \mathbf c\in\mathbb R^d c ∈ R d 可学习参数 ,称为 Attention Vector。实际上它就是一个代理query ,用来从和特征向量求相似度以从中获取关于模态p p p
PyTorch 实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Attention (nn.Module): def __init__ (self, dim, heads = 8 , dim_head = 64 , dropout = 0. ): ''' dim: 输入维度 heads: 多头注意力的头的个数 dim_head: 每个头的输出维度 dropout: dropout比率 ''' super ().__init__() inner_dim = dim_head * heads project_out = not (heads == 1 and dim_head == dim) self.heads = heads self.scale = dim_head ** -0.5 self.norm = nn.LayerNorm(dim) self.attend = nn.Softmax(dim = -1 ) self.dropout = nn.Dropout(dropout) self.to_qkv = nn.Linear(dim, inner_dim * 3 , bias = False ) self.to_out = nn.Sequential( nn.Linear(inner_dim, dim), nn.Dropout(dropout) ) if project_out else nn.Identity() def forward (self, x ): x = self.norm(x) qkv = self.to_qkv(x).chunk(3 , dim = -1 ) q, k, v = map (lambda t: rearrange(t, 'b n (h d) -> b h n d' , h = self.heads), qkv) dots = torch.matmul(q, k.transpose(-1 , -2 )) * self.scale attn = self.attend(dots) attn = self.dropout(attn) out = torch.matmul(attn, v) out = rearrange(out, 'b h n d -> b n (h d)' ) return self.to_out(out)
稀疏 Attention 从理论上来讲,Self Attention的计算时间和显存占用量都是O ( n 2 ) \mathcal{O}(n^2) O ( n 2 ) n n n 二次复杂性 的问题。这就意味着如果序列长度n n n
Self Attention 的二次复杂性主要来源于它要对序列中的任意两个向量都计算相关度,最后生成n × n n\times n n × n 稀疏Attention 的基本原理。
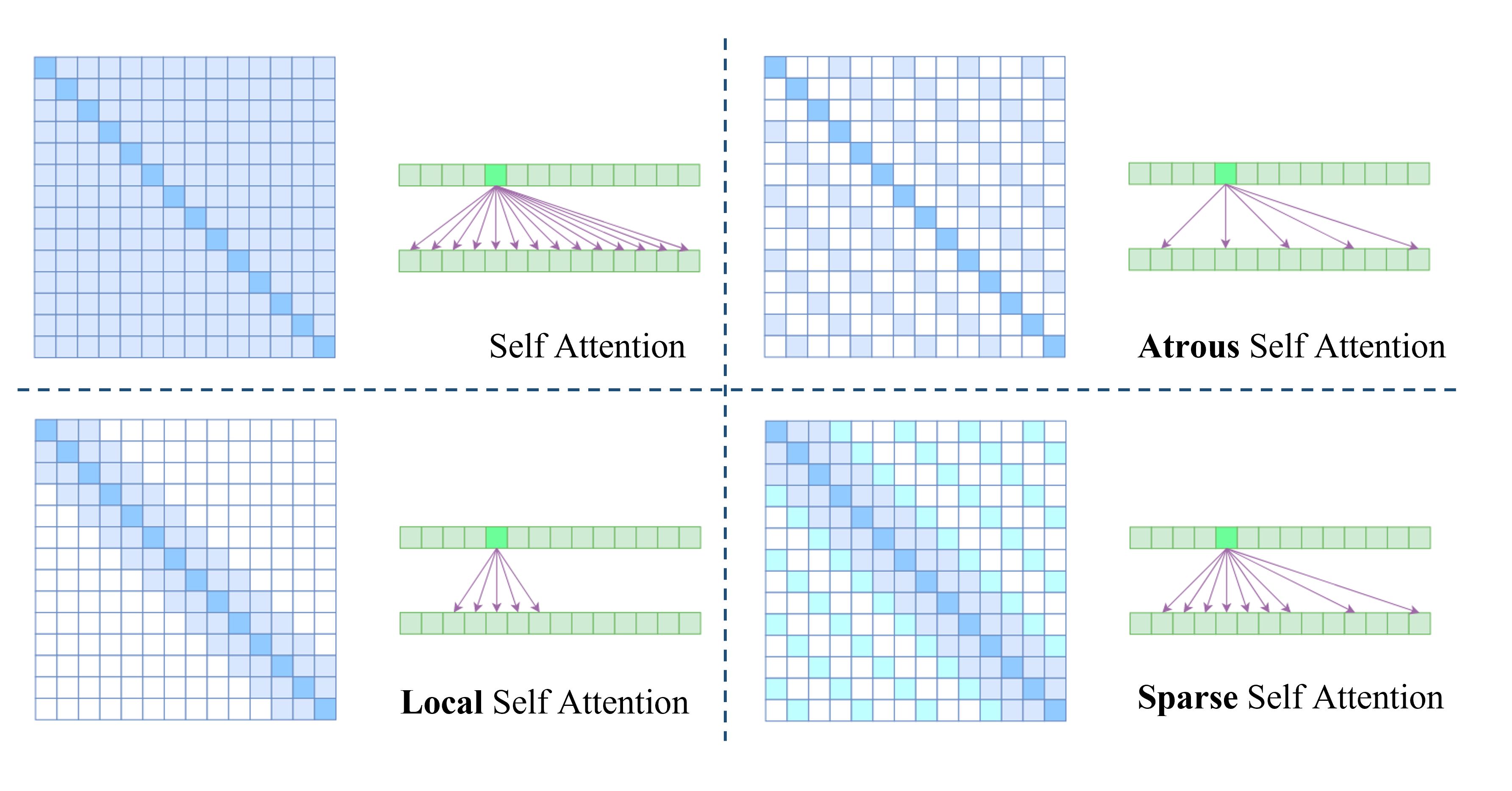
上图列出了在减少计算性上已有的部分工作,命名方式参考了苏剑林苏神 。
Atrous Self Attention 很显然参考了空洞卷积(Atrous Convolution),强行要求每个元素只跟它相对距离为k , 2 k , 3 k , … k,2k,3k,… k , 2 k , 3 k , … k > 1 k>1 k > 1 Local Self Attention 约束每个元素只与前后k k k Sparse Self Attention 由 OpenAI 提出,直接将Atrous Self Attention和Local Self Attention合并在一起,这样一来Attention就具有“局部紧密相关和远程稀疏相关 ”的特性,这对很多任务来说可能是一个不错的先验,因为真正需要密集的长程关联的任务事实上是很少的。虽然这种思路切实能提高效率,但是也存在两个明显的不足之处:
如何选择要保留的注意力区域,这是人工主观决定的,带有很大的不智能性; 需要从编程上进行特定的设计优化,才能得到一个高效的实现,不容易推广。 还有一些经典工作也是延续了稀疏化矩阵的思想展开的,比如 Longformer 和 BigBird 等。
📃 Reformer: The Efficient Transformer
Reformer 致力于解决传统 Transformer 的以下三种问题在工程中面临的挑战:
Attention 计算的二次复杂性(使用 LSH Attention); 多层 Transformer Block 在反向传播时产生的内存开销(使用 RevNet); 前馈网络的深度造成的内存开销(分块计算). Reformer 通过引入 局部敏感哈希 (Locality-Sensitive Hashing, LSH)算法来解决二次复杂性问题。
LSH 的背景是实现海量高维数据的近似最近邻快速搜索 (Approximate Nearest Neighbor, ANN),由 Indyk-Motwani 在1998年引入。想象一下,当我们需要寻找相似的向量对时,即使在样本量不高的数据集上,比较所有向量所需的计算量至多也是O ( N ) O(N) O ( N ) 向量索引 ,那么最佳排序方法则优化为了对数线性时间复杂度O ( N log N ) O(N\log N) O ( N log N ) 减少比较次数 的方法呢?甚至理想情况下,我们只想比较我们认为是潜在匹配的向量(候选对) ,而 LSH 则实现了这样的想法.
LSH 的核心思想是:寻求一种哈希函数,使得原本的向量空间中就相邻和接近的向量通过哈希映射之后还能有很大可能性被放入同一个桶中 。这样的哈希函数就是“局部敏感”的。d d d p , q \boldsymbol{p},\boldsymbol{q} p , q
Pr [ h ( p ) = h ( q ) ] ≈ d ( p , q ) \Pr[h(\boldsymbol{p})=h(\boldsymbol{q})]\approx d(\boldsymbol{p},\boldsymbol{q}) Pr [ h ( p ) = h ( q )] ≈ d ( p , q )
其中h ( ⋅ ) h(·) h ( ⋅ )
【定义 】一个( r , R , α , β ) -sensitive (r,R,\alpha,\beta)\text{-sensitive} ( r , R , α , β ) -sensitive H H H h ∈ H h\in H h ∈ H p , q ∈ R d \boldsymbol{p},\boldsymbol{q}\in\mathbb{R}^d p , q ∈ R d r < R , 0 < α < β < 1 r<R,\; 0<\alpha<\beta<1 r < R , 0 < α < β < 1
如果p ∈ Ball ( q , r ) \boldsymbol{p}\in \text{Ball}(\boldsymbol{q},r) p ∈ Ball ( q , r ) Pr [ h ( p ) = h ( q ) ] ≥ α \Pr[h(\boldsymbol{p})=h(\boldsymbol{q})]\geq\alpha Pr [ h ( p ) = h ( q )] ≥ α 如果p ∈ Ball ( q , R ) \boldsymbol{p}\in \text{Ball}(\boldsymbol{q},R) p ∈ Ball ( q , R ) Pr [ h ( p ) = h ( q ) ] ≤ β \Pr[h(\boldsymbol{p})=h(\boldsymbol{q})]\leq\beta Pr [ h ( p ) = h ( q )] ≤ β 说人话就是,向量p \boldsymbol{p} p q \boldsymbol{q} q r r r R R R α \alpha α β \beta β
为了减少漏报率(就是本来很相近的两条数据被认为是不相似的),一种常用的解决方案是采用用多个哈希函数(即使用哈希表)来映射向量,然后对结果进行指定操作(AND、OR、XOR 等)从而得到最终的结果。
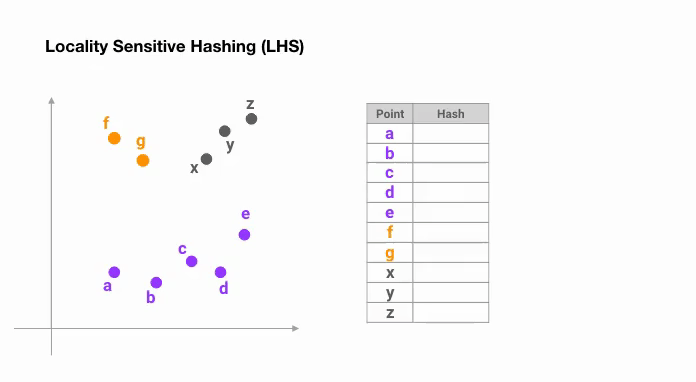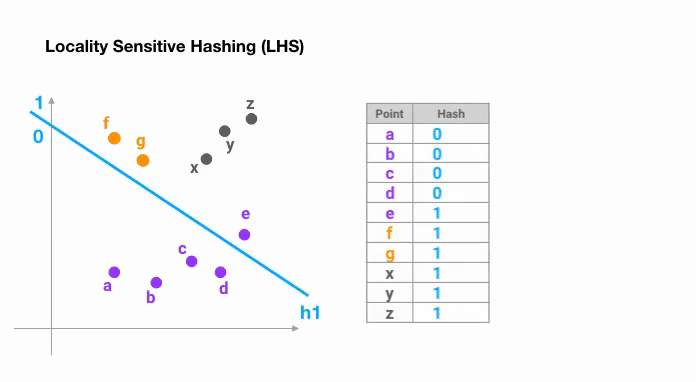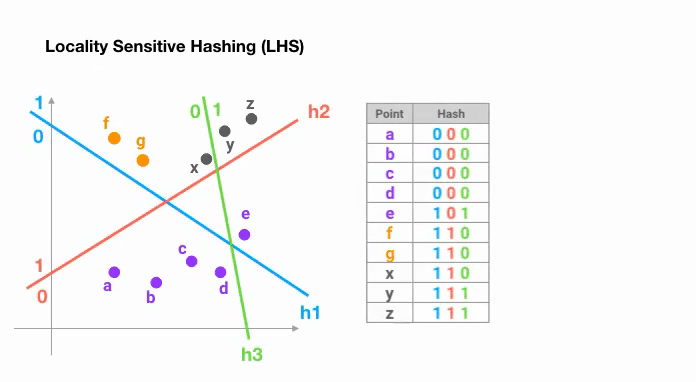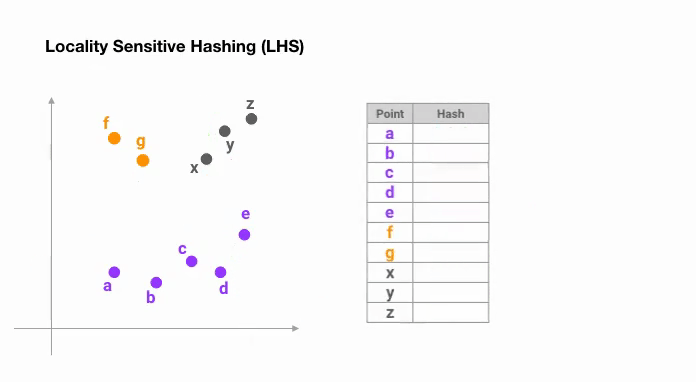
下图展示了一个在二维空间中随机 划分超平面,然后使用sign ( p ⊤ H ) \text{sign}(\boldsymbol{p}^\top H) sign ( p ⊤ H )
Reformer 引入了 Angular LSH 来构造哈希,简单来说就是把d d d
上图展示了一个在 2D 平面上经过 3次随机选择后,两个点x , y x,y x , y
最终,将这种机制应用于 Attention 中,即不计算Q Q Q K K K
计算Q Q Q K K K 只计算相同哈希桶中的k k k q q q 一个包括原始注意力和自注意力的示例如下图所示:
【总结 】相比前述稀疏Attention,Reformer解决了它的第一个缺点,即实现了自动选择需要保留注意力的区域。但是它依然有难以实现这一缺点,具体来说,要实现LSH形式的Attention比标准的Attention复杂得多,而且对可逆网络重写反向传播过程对普通读者来说更是遥不可及。
更多相关文献解读:💡Illustrating the Reformer. 🚊 ️ The efficient Transformer | by Alireza Dirafzoon | Towards Data Science | 中文翻译 Reformer: 局部敏感哈希、可逆残差和分块计算带来的高效 - 知乎
Linear Attention 📃 Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention 线性Attention的探索:Attention必须有个Softmax吗? - 科学空间
Self Attention具有二次复杂性 问题追根溯源还是绕不开矩阵相乘上,即
softmax ( Q K ⊤ ) V \begin{aligned} \operatorname{softmax}\left(QK^\top\right)V \end{aligned} softmax ( Q K ⊤ ) V
其中的Q K ⊤ QK^\top Q K ⊤
而事实上,如果没有 Softmax ,那么就是三个矩阵连乘Q K ⊤ V QK^\top V Q K ⊤ V 结合律 ,所以我们可以先计算K ⊤ V K^\top V K ⊤ V d × d d\times d d × d Q Q Q d ≪ n d \ll n d ≪ n O ( n ) \mathcal{O}(n) O ( n )
论文通过引入新的相似性函数 代替原本的高斯核 以达到消去 softmax 的目的。
Attention ( Q , K , V ) i = ∑ j = 1 n sim ( q i , k j ) v j ∑ j = 1 n sim ( q i , k j ) \text{Attention}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i = \frac{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)\boldsymbol{v}_j}{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)} Attention ( Q , K , V ) i = j = 1 ∑ n sim ( q i , k j ) j = 1 ∑ n sim ( q i , k j ) v j
具体来说,就是把原版的e q ⊤ k e^{q^\top k} e q ⊤ k sim ( q i , k i ) \text{sim}(q_i,k_i) sim ( q i , k i ) 相似性函数的值域非负 。
论文作者提出直接用内积做相似性度量方式,但是由于两个向量的内积无法保证结果非负,所以又在外面套了一层激活函数/核函数然后再让两个向量做内积 。即:
sim ( q i , k i ) = ψ ( q i ) ⊤ ϕ ( k i ) \text{sim}(q_i,k_i)=\psi(q_i)^\top\phi(k_i) sim ( q i , k i ) = ψ ( q i ) ⊤ ϕ ( k i )
其中,只要保证激活函数的值域非负即可。ψ ( x ) = ϕ ( x ) = elu ( x ) + 1 \psi(x)=\phi(x)=\text{elu}(x)+1 ψ ( x ) = ϕ ( x ) = elu ( x ) + 1
那么,论文标题说的 Transformer 作为 RNN 实现自回归又从何谈起呢?实际上当做了上述的线性化处理之后,代入原始公式,有:
Attention ( Q , K , V ) i = ∑ j = 1 i ( ϕ ( q i ) ⊤ φ ( k j ) ) v j ∑ j = 1 i ϕ ( q i ) ⊤ φ ( k j ) = ϕ ( q i ) ⊤ ∑ j = 1 i φ ( k j ) v j ⊤ ϕ ( q i ) ⊤ ∑ j = 1 i φ ( k j ) \text{Attention}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i = \frac{\sum\limits_{j=1}^i \left(\phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)\right)\boldsymbol{v}_j}{\sum\limits_{j=1}^i \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)}=\frac{ \phi(\boldsymbol{q}_i)^{\top} \sum\limits_{j=1}^i\varphi(\boldsymbol{k}_j)\boldsymbol{v}_j^{\top}}{ \phi(\boldsymbol{q}_i)^{\top} \sum\limits_{j=1}^i\varphi(\boldsymbol{k}_j)} Attention ( Q , K , V ) i = j = 1 ∑ i ϕ ( q i ) ⊤ φ ( k j ) j = 1 ∑ i ( ϕ ( q i ) ⊤ φ ( k j ) ) v j = ϕ ( q i ) ⊤ j = 1 ∑ i φ ( k j ) ϕ ( q i ) ⊤ j = 1 ∑ i φ ( k j ) v j ⊤
更进一步,令S i = ∑ j = 1 i φ ( k j ) v j ⊤ \boldsymbol{S}_i=\sum\limits_{j=1}^i\varphi(\boldsymbol{k}_j)\boldsymbol{v}_j^{\top} S i = j = 1 ∑ i φ ( k j ) v j ⊤ z i = ∑ j = 1 i φ ( k j ) \boldsymbol{z}_i=\sum\limits_{j=1}^i\varphi(\boldsymbol{k}_j) z i = j = 1 ∑ i φ ( k j )
Attention ( Q , K , V ) i = ϕ ( q i ) ⊤ S i ϕ ( q i ) ⊤ z i , S i = S i − 1 + φ ( k i ) v i ⊤ z i = z i − 1 + φ ( k i ) \text{Attention}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i =\frac{ \phi(\boldsymbol{q}_i)^{\top} \boldsymbol{S}_i}{ \phi(\boldsymbol{q}_i)^{\top} \boldsymbol{z}_i},\quad \begin{aligned}&\boldsymbol{S}_i=\boldsymbol{S}_{i-1}+\varphi(\boldsymbol{k}_i)\boldsymbol{v}_i^{\top}\\ &\boldsymbol{z}_i=\boldsymbol{z}_{i-1}+\varphi(\boldsymbol{k}_i) \end{aligned} Attention ( Q , K , V ) i = ϕ ( q i ) ⊤ z i ϕ ( q i ) ⊤ S i , S i = S i − 1 + φ ( k i ) v i ⊤ z i = z i − 1 + φ ( k i )
也就是说我们可以使用递归迭代 的方式来计算第i i i 适合预测 的时候进行解码。
从另一个角度看,可以直接对φ ( K ) , V ∈ R n × d \varphi(\boldsymbol{K}),\boldsymbol{V}\in\mathbb{R}^{n\times d} φ ( K ) , V ∈ R n × d n × d × d n\times d\times d n × d × d n n n cumsum 运算,就可以一次性得到S i , ∀ i \boldsymbol{S}_i, \forall i S i , ∀ i 适合训练 时使用。
其实类似的思考角度在 SSM 中也有所体现,可以用参考本站对 状态空间模型与Mamba的前世今生 的博客记录。
📃Rethinking Attention with Performers
参考前面几节的内容,我们知道,从公式上将注意力机制线性化的一般“套路”就是给出合适的相似性度量sim ( q , k ) \text{sim}(q,k) sim ( q , k ) Performer 指出可以通过随机投影,在不损失精度 的情况下,将Attention的复杂度线性化 。
考虑到不损失精度,Performer 沿用了 Transformer 的相似性度量方式,即:
sim ( q , k ) = e q ⋅ k \text{sim}(q,k)=e^{q\cdot k} sim ( q , k ) = e q ⋅ k
然后它希望将复杂度线性化,那就是需要找到新的q ~ , k ~ \tilde{q},\tilde{k} q ~ , k ~
e q ⋅ k ≈ q ~ ⋅ k ~ e^{q\cdot k}\approx\tilde{q}\cdot\tilde{k} e q ⋅ k ≈ q ~ ⋅ k ~
Performer的最大贡献就在于,它真的找到了一个非常漂亮的映射方案:
e q ⋅ k = E ω ∼ N ( ω ; 0 , 1 d ) [ e ω ⋅ q − ∥ q ∥ 2 / 2 × e ω ⋅ k − ∥ k ∥ 2 / 2 ] ≈ 1 m ( e ω 1 ⋅ q − ∥ q ∥ 2 / 2 e ω 2 ⋅ q − ∥ q ∥ 2 / 2 ⋮ e ω m ⋅ q − ∥ q ∥ 2 / 2 ) ⏟ q ~ ⋅ 1 m ( e ω 1 ⋅ k − ∥ k ∥ 2 / 2 e ω 2 ⋅ k − ∥ k ∥ 2 / 2 ⋮ e ω m ⋅ k − ∥ k ∥ 2 / 2 ) ⏟ k ~ \begin{aligned} e^{\boldsymbol{q}\cdot \boldsymbol{k}}&=\mathbb{E}_{\boldsymbol{\omega}\sim \mathcal{N}(\boldsymbol{\omega};0,\boldsymbol{1}_d)}\left[e^{\boldsymbol{\omega}\cdot \boldsymbol{q}-\Vert \boldsymbol{q}\Vert^2 / 2} \times e^{\boldsymbol{\omega}\cdot \boldsymbol{k}-\Vert \boldsymbol{k}\Vert^2 / 2}\right]\\[6pt] &\approx\underbrace{\frac{1}{\sqrt{m}}\begin{pmatrix}e^{\boldsymbol{\omega}_1\cdot \boldsymbol{q}-\Vert \boldsymbol{q}\Vert^2 / 2} \\ e^{\boldsymbol{\omega}_2\cdot \boldsymbol{q}-\Vert \boldsymbol{q}\Vert^2 / 2}\\ \vdots\\ e^{\boldsymbol{\omega}_m\cdot \boldsymbol{q}-\Vert \boldsymbol{q}\Vert^2 / 2} \end{pmatrix}}_{\tilde{\boldsymbol{q}}} \cdot \underbrace{\frac{1}{\sqrt{m}}\begin{pmatrix}e^{\boldsymbol{\omega}_1\cdot \boldsymbol{k}-\Vert \boldsymbol{k}\Vert^2 / 2} \\ e^{\boldsymbol{\omega}_2\cdot \boldsymbol{k}-\Vert \boldsymbol{k}\Vert^2 / 2}\\ \vdots\\ e^{\boldsymbol{\omega}_m\cdot \boldsymbol{k}-\Vert \boldsymbol{k}\Vert^2 / 2} \end{pmatrix}}_{\tilde{\boldsymbol{k}}} \end{aligned} e q ⋅ k = E ω ∼ N ( ω ; 0 , 1 d ) [ e ω ⋅ q − ∥ q ∥ 2 /2 × e ω ⋅ k − ∥ k ∥ 2 /2 ] ≈ q ~ m 1 e ω 1 ⋅ q − ∥ q ∥ 2 /2 e ω 2 ⋅ q − ∥ q ∥ 2 /2 ⋮ e ω m ⋅ q − ∥ q ∥ 2 /2 ⋅ k ~ m 1 e ω 1 ⋅ k − ∥ k ∥ 2 /2 e ω 2 ⋅ k − ∥ k ∥ 2 /2 ⋮ e ω m ⋅ k − ∥ k ∥ 2 /2
其中,ω ∼ N ( ω ; 0 , 1 d ) \boldsymbol{\omega}\sim \mathcal{N}(\boldsymbol{\omega};0,\boldsymbol{1}_d) ω ∼ N ( ω ; 0 , 1 d ) m m m q ~ , k ~ \tilde{q},\tilde{k} q ~ , k ~
相关证明和推导:Performer:用随机投影将Attention的复杂度线性化 n维空间下两个随机向量的夹角分布 更多的近似方案:作为无限维的线性Attention
跟Performer相比,Nyströmformer去除了线性化过程中的随机性,因为Performer是通过随机投影来达到线性化的,这必然会带来随机性。对于某些有强迫症的读者来说,这个随机性可能是难以接受的存在,而Nyströmformer则不存在这种随机性,因此也算是一个亮点。
Nyströmformer:基于矩阵分解的线性化Attention方案 - 科学空间|Scientific Spaces (kexue.fm)
VQ一下Key,Transformer的复杂度就变成线性了 - 科学空间|Scientific Spaces (kexue.fm)
FLASH FLASH:可能是近来最有意思的高效Transformer设计 - 科学空间|Scientific Spaces (kexue.fm) GAU-α:尝鲜体验快好省的下一代Attention - 科学空间|Scientific Spaces 高效 Transformer:从 GLU 到 GAU - 小昇的博客
番外篇 Self-attention vs. CNN 论文 《On the Relationship between Self-Attention andConvolutional Layers》 (https://arxiv.org/abs/1911.03584)指出,CNN其实就是自注意力机制的一种特例。
Synthesizer 📃Synthesizer: Rethinking Self-Attention in Transformer Models
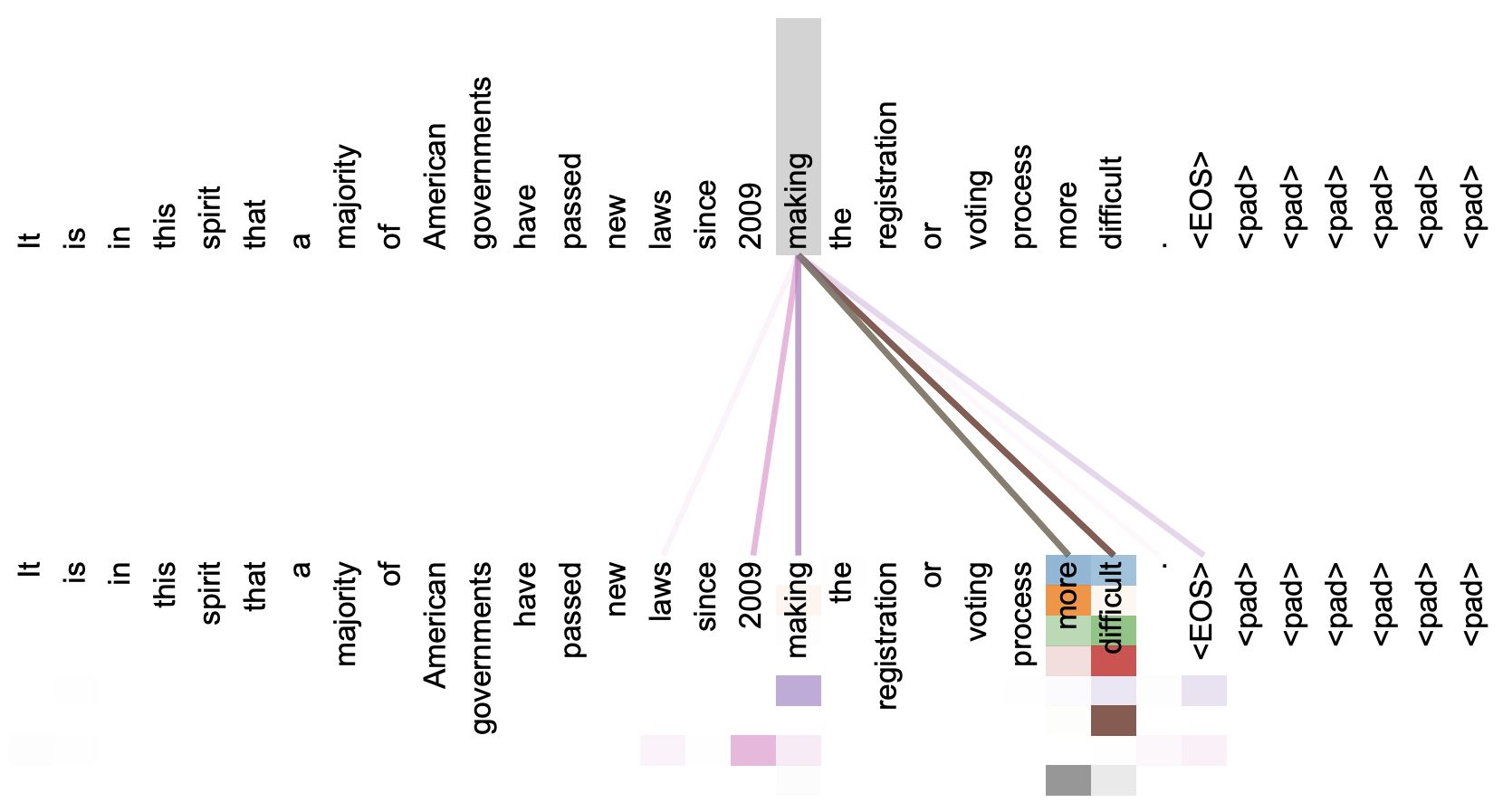
直观上来看,自注意力机制算是解释性比较强 的模型之一了,它通过自己与自己的Attention来自动捕捉了token与token之间的关联。通过可视化注意力矩阵我们也可以直观看到这一点,因此这也是科研中用来做模型可解释性的有利可视化工具。
事实上在Transformer原论文中,就给出了如下的看上去挺合理的可视化效果:
然而,Google发表的这篇论文对自注意力机制做了一些“异想天开”的探索。
为了讨论方便,原论文将自注意力机制所需的矩阵简记如下:
A = softmax ( B ) , B = X W q W k ⊤ X ⊤ d k \boldsymbol{A}=\text{softmax}\left(\boldsymbol{B}\right),\quad\boldsymbol{B}=\frac{\boldsymbol{X}\boldsymbol{W}_q \boldsymbol{W}_k^{\top}\boldsymbol{X}^{\top}}{\sqrt{d_k}} A = softmax ( B ) , B = d k X W q W k ⊤ X ⊤
然后,这项研究直接不考虑输入数据之间的关联 ,将矩阵B ∈ R n × n \boldsymbol B\in\mathbb{R}^{n\times n} B ∈ R n × n B \boldsymbol B B Dense 和 Random 形式。更进一步,还验证了对两种形式的低秩分解,还有混合两种形式来参与模型训练。
最终实验证明,这样训练出来的模型居然还和原版 Transformer 有着旗鼓相当 的性能,而且相应的效率更高。只可惜在迁移性上效果不佳 ,而其解释性就无从谈起了。实验结果很可能冲击了我们对自注意力机制的已有认知,值得思考。
Google新作Synthesizer:我们还不够了解自注意力 - 科学空间
Att的Bug? 待更:https://zhuanlan.zhihu.com/p/645922048 https://www.evanmiller.org/attention-is-off-by-one.html
低秩问题? Transformer升级之路:3、从Performer到线性Attention - 科学空间|Scientific Spaces (kexue.fm)
参考 动手学习深度学习|D2L Discussion - Dive into Deep Learning 详解深度学习中的注意力机制(Attention) - 知乎 拆 Transformer 系列二:Multi- Head Attention 机制详解 【李宏毅机器学习2021】自注意力机制 (Self-attention) -bilibili 为节约而生:从标准Attention到稀疏Attention - 科学空间 线性Attention的探索:Attention必须有个Softmax吗? - 科学空间 Performer:用随机投影将Attention的复杂度线性化 - 科学空间