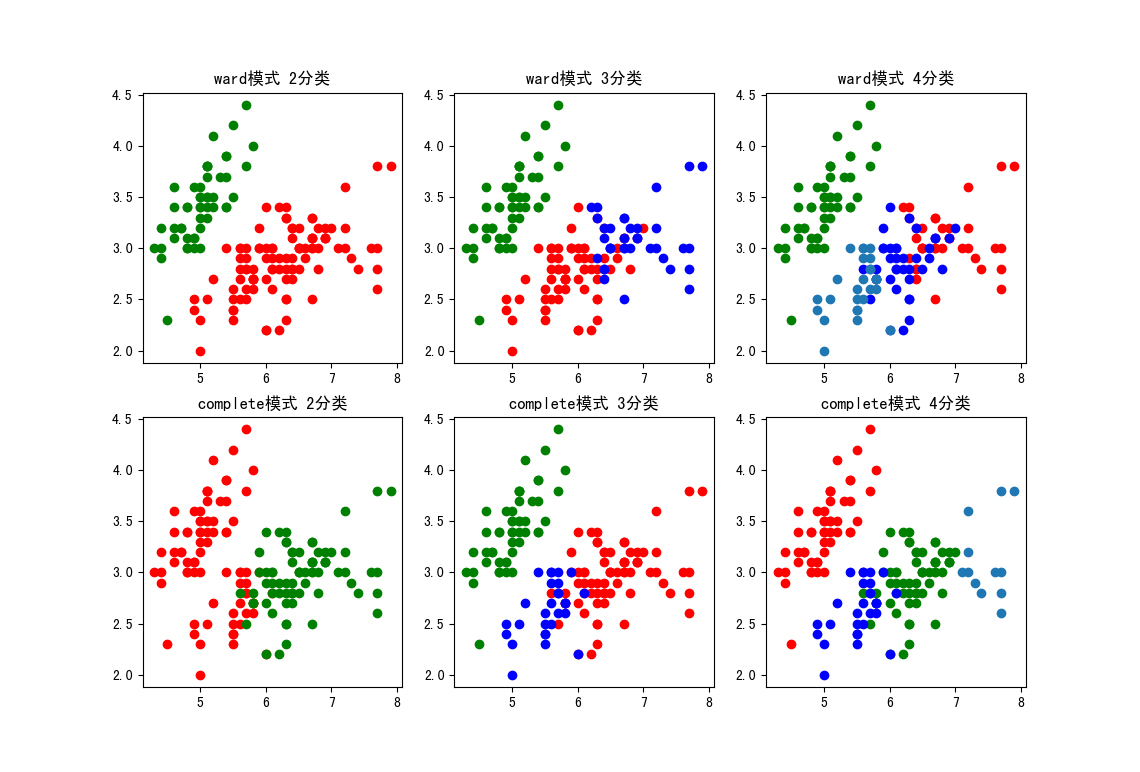
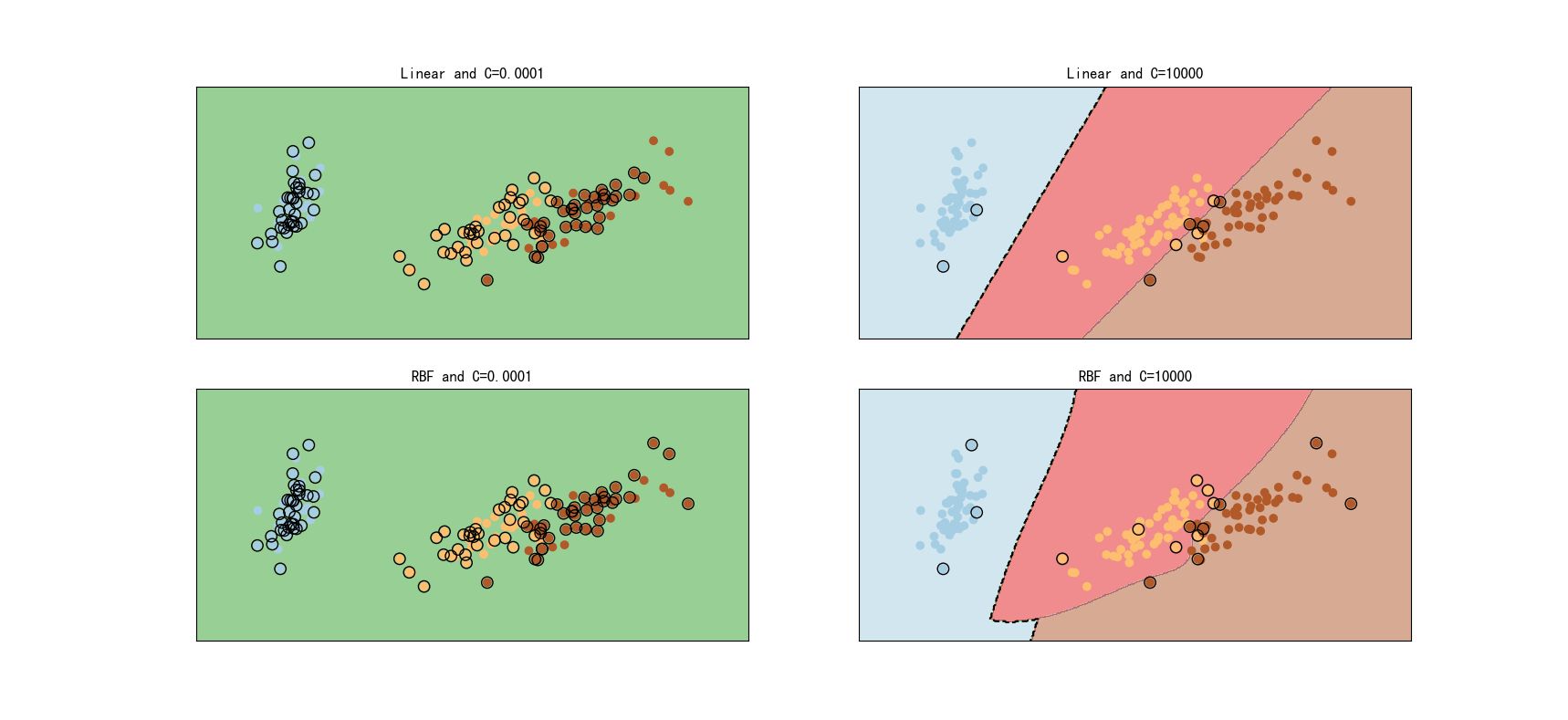
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| import numpy as np
from sklearn import svm
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def PCA(data, n):
from sklearn.decomposition import PCA
pca = PCA(n_components=n)
pca_result = pca.fit_transform(data)
return pca_result
def plot(target,pca_result,title):
plt.scatter(pca_result[target == 0, 0], pca_result[target == 0, 1], color='r')
plt.scatter(pca_result[target == 1, 0], pca_result[target == 1, 1], color='g')
plt.scatter(pca_result[target == 2, 0], pca_result[target == 2, 1], color='b')
plt.title(title)
if __name__ == '__main__':
iris = load_iris()
pca_result = PCA(iris.data,2)
X_train, X_test, y_train, y_test = train_test_split(pca_result, iris.target,
test_size=0.3,
random_state=0)
lin_svc1 = svm.SVC(kernel='linear',C=0.0001).fit(X_train, y_train)
lin_svc2 = svm.SVC(kernel='linear',C=10000).fit(X_train, y_train)
lin_svc1 = svm.SVC(kernel='linear',C=0.0001).fit(X_train, y_train)
rbf_svc1 = svm.SVC(kernel='rbf',C=0.0001).fit(X_train, y_train)
rbf_svc2 = svm.SVC(kernel='rbf',C=10000).fit(X_train, y_train)
h = .02
x_min, x_max = X_train[:, 0].min() - 1, X_train[:, 0].max() + 1
y_min, y_max = X_train[:, 1].min() - 1, X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
titles = ['Linear and C=0.0001','Linear and C=10000',
'RBF and C=0.0001','RBF and C=10000']
for i, clf in enumerate(( lin_svc1, lin_svc2,rbf_svc1,rbf_svc2)):
xy = np.c_[xx.ravel(),yy.ravel()]
Z = clf.predict(xy)
Z = Z.reshape(xx.shape)
plt.subplot(2, 2, i + 1)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.5)
plt.contour(xx,yy,Z,colors=['k','k','k'],levels=[-125,0,125],linestyles=['--','-','--'])
plt.scatter(pca_result[:, 0], pca_result[:, 1], c=iris.target, cmap=plt.cm.Paired)
plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1], s=80,facecolors='none', edgecolors='k')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.title(titles[i])
plt.show()
|