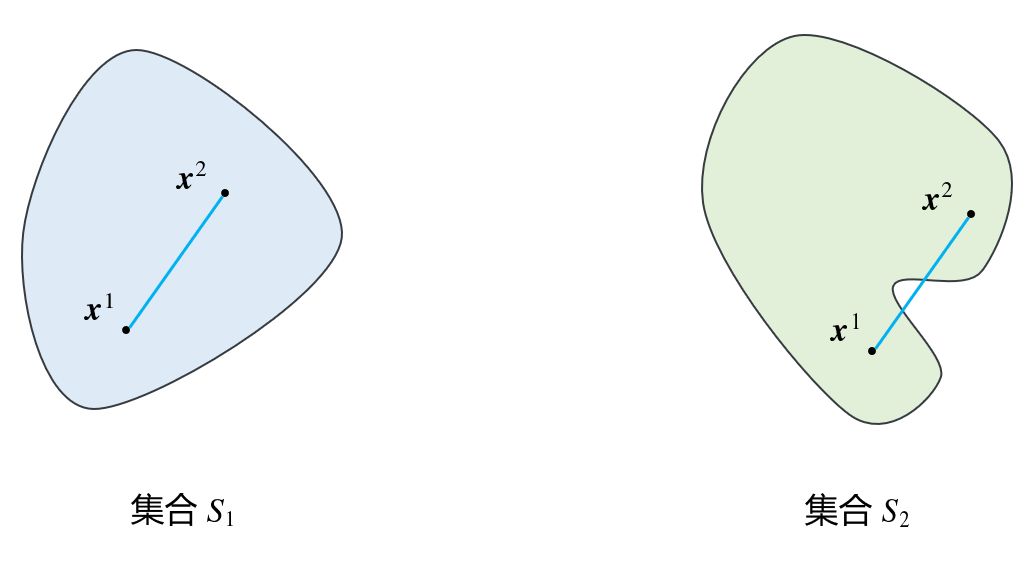
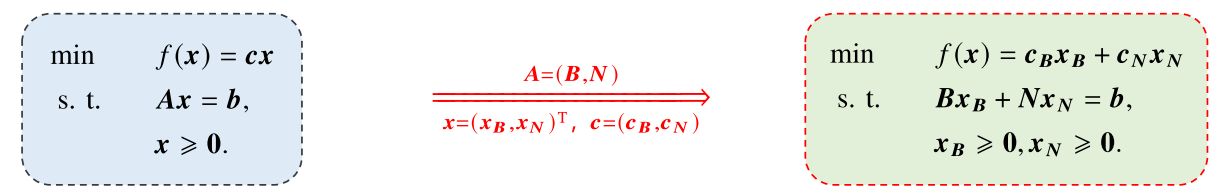凸集 | Convex Set 定义 设S ⊂ R n S\subset\Bbb R^n S ⊂ R n n n n S S S x 1 , x 2 ∈ S \boldsymbol x_1,\boldsymbol x_2\in S x 1 , x 2 ∈ S S S S λ ∈ [ 0 , 1 ] \lambda\in[0,1] λ ∈ [ 0 , 1 ]
λ x 1 + ( 1 − λ ) x 2 ∈ S \lambda\boldsymbol x_1+(1-\lambda)\boldsymbol x_2\in S λ x 1 + ( 1 − λ ) x 2 ∈ S
则称集合S S S 凸集 ,称λ x 1 + ( 1 − λ ) x 2 \lambda\boldsymbol x_1+(1-\lambda)\boldsymbol x_2 λ x 1 + ( 1 − λ ) x 2 x 1 , x 2 \boldsymbol x_1,\boldsymbol x_2 x 1 , x 2 凸组合 。
定义 集合 C C C 凸包 是 C C C conv C \text{conv }C conv C
Note: 当λ ∈ R \lambda\in\Bbb R λ ∈ R 仿射 集合(Affine sets ),对应的线性组合也叫仿射组合,另外还有仿射包。
e.g. 上图中,S 1 S_1 S 1 S 2 S_2 S 2
常见的凸集 超平面 | Hyperplane 我们知道,以x y z xyz x yz a x + b y + c z = d ax+by+cz=d a x + b y + cz = d { ( x , y , z ) ∣ a x + b y + c z = d } \{(x,y,z)|ax+by+cz=d\} {( x , y , z ) ∣ a x + b y + cz = d }
将这种概念拓展到多维空间中时,我们可以定义满足p T x = α \boldsymbol p^T\boldsymbol x=\alpha p T x = α n n n x ∈ R n \boldsymbol x\in\Bbb R^n x ∈ R n 超平面 :H = { x ∣ p T x = α } H=\{\boldsymbol x|\boldsymbol p^T\boldsymbol x=\alpha\} H = { x ∣ p T x = α }
可以证明超平面是一个凸集 .
半空间 & Others 不难想象,一个超平面可以把一个空间一分为二,而超平面往下的部分或者另一边的部分就是一个半空间 (Half space)。用数学形式表示:H − = { x ∣ p T x ≤ α } H^-=\{\boldsymbol x|\boldsymbol p^T\boldsymbol x\leq\alpha\} H − = { x ∣ p T x ≤ α }
可以证明半空间是一个凸集 .
【多面体 】有限个半空间的 交 我们称为多面体 (Polyhedron),其约束可以写为:
( p 1 T p 2 T ⋮ p n T ) x ≤ ( b 1 b 2 ⋮ b n ) ⇔ A x ≤ b \begin{aligned} \begin{pmatrix}\boldsymbol p_1^T\\\boldsymbol p_2^T\\\vdots\\\boldsymbol p_n^T\end{pmatrix}\boldsymbol x \leq\begin{pmatrix}b_1\\b_2\\\vdots\\b_n\end{pmatrix}\Leftrightarrow\boldsymbol {Ax\leq b} \end{aligned} p 1 T p 2 T ⋮ p n T x ≤ b 1 b 2 ⋮ b n ⇔ Ax ≤ b
多面体也是凸集 。
【射线 】以某一定点 x ( 0 ) \boldsymbol x^{(0)} x ( 0 ) d \boldsymbol d d 射线 :L = { x ∣ x = x ( 0 ) + λ d , λ ≥ 0 } L=\{\boldsymbol x|\boldsymbol x=\boldsymbol x^{(0)}+\lambda\boldsymbol d,\;\lambda\geq0\} L = { x ∣ x = x ( 0 ) + λ d , λ ≥ 0 } d \boldsymbol d d
【凸锥 】若集合C ⊂ R n C\subset\Bbb R^n C ⊂ R n x \boldsymbol x x λ \lambda λ λ x ∈ C \lambda\boldsymbol x\in C λ x ∈ C C C C 锥 (Cone)。当C C C 凸锥 (convex cone)。
在多面集的表达式中,若b = 0 \boldsymbol {b=0} b = 0 多面锥 。
单纯形 | Simplex 单纯形是一种特殊的多面体 。它之所以叫“单纯形”,是因为它是该维度上“最简单”的多面体。几何上,单纯形是三角形或四面体在任意维度的推广。
定义 设 k + 1 k+1 k + 1 x 0 , . . . , x k \boldsymbol x_0,...,\boldsymbol x_k x 0 , ... , x k 仿射独立 ,即 x 1 − x 0 , . . . , x k − x 0 \boldsymbol x_1−\boldsymbol x_0, ... ,\boldsymbol x_k−\boldsymbol x_0 x 1 − x 0 , ... , x k − x 0
C = conv { x 0 , ⋯ , x k } = { λ 0 x 0 + ⋯ + λ k x k ∣ λ ≥ 0 , ∑ i = 0 k λ i = 1 } C=\text{conv}\{\boldsymbol x_0,\cdots,\boldsymbol x_k\}=\{\lambda_0\boldsymbol x_0+\cdots+\lambda_k\boldsymbol x_k\mid\lambda\geq0,\sum_{i=0}^k\lambda_i=1\} C = conv { x 0 , ⋯ , x k } = { λ 0 x 0 + ⋯ + λ k x k ∣ λ ≥ 0 , i = 0 ∑ k λ i = 1 }
这个单纯形的仿射维度为 k k k R n \Bbb R^n R n k k k
仿射维度k k k 几何形态 0 点 1 线段 2 三角形 3 四面体 4 5-cell … …
单纯形与单纯形方法的关系
单纯形方法中并没有用到单纯形。那为什么单纯形方法会如此命名呢?
欧氏球 | Euclidean balls B ( x c , r ) = { x ∣ ∣ ∣ x − x c ∣ ∣ 2 ≤ r } = { x c + r u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } B(\boldsymbol x_{c},r)=\{\boldsymbol x \mid ||\boldsymbol x-\boldsymbol x_{c} ||_{2}{\;\leq\;} r \}=\{\boldsymbol x_{c}+ru \mid || u ||_{2}{\;\leq\;}1\} B ( x c , r ) = { x ∣ ∣∣ x − x c ∣ ∣ 2 ≤ r } = { x c + r u ∣ ∣∣ u ∣ ∣ 2 ≤ 1 } x c \boldsymbol x_c x c r r r L 2 L2 L 2 欧氏球是凸集 。
事实上这可以扩展到任意范数,都能证明其为凸集,推导原理是三角不等式。类似地,还可以得出各种范数里的椭球也是凸集 。
常见性质 设S 1 , S 2 ⊂ R n S_1,S_2\subset\Bbb R^n S 1 , S 2 ⊂ R n β \beta β
β S 1 = { β x ∣ x ∈ S 1 } \beta S_1=\{\beta\boldsymbol x|\boldsymbol x\in S_1\} β S 1 = { β x ∣ x ∈ S 1 } S 1 ∩ S 2 S_1\cap S_2 S 1 ∩ S 2 S 1 + S 2 = { x ( 1 ) + x ( 2 ) ∣ x ( 1 ) ∈ S 1 , x ( 2 ) ∈ S 2 } S_1+S_2=\{\boldsymbol x^{(1)}+\boldsymbol x^{(2)}|\boldsymbol x^{(1)}\in S_1,\boldsymbol x^{(2)}\in S_2\} S 1 + S 2 = { x ( 1 ) + x ( 2 ) ∣ x ( 1 ) ∈ S 1 , x ( 2 ) ∈ S 2 } S 1 − S 2 S_1-S_2 S 1 − S 2 事实上,以上限制进一步推广就是保凸运算 。此处不过多展开,可参考前面提到的开源课程或者下面的博客。
凸优化 - 凸集 - Infinity-SEU 凸集 - 水论文的程序猿
极点与极方向 定义 设 S ⊂ R n S\subset\Bbb R^n S ⊂ R n x ∈ S x\in S x ∈ S S S S 极点 ,当且仅当 ∄ x 1 , x 2 ∈ S ( x 1 ≠ x 2 ) , λ ∈ ( 0 , 1 ) \not\exists x_1,x_2\in S\;(x_1≠x_2),\;\lambda∈(0,1) ∃ x 1 , x 2 ∈ S ( x 1 = x 2 ) , λ ∈ ( 0 , 1 ) x = λ x 1 + ( 1 − λ ) x 2 x=\lambda x_1+(1−\lambda)x_2 x = λ x 1 + ( 1 − λ ) x 2
即极点不能用凸集中两个不同的点的严格凸组合 表示。(注意λ ≠ 0 , 1 \lambda\neq0,1 λ = 0 , 1 )
Note: 为了书写方便,此处(甚至以后)的向量和矩阵在不会引起歧义的情况下都不再通过加粗的方式板书。
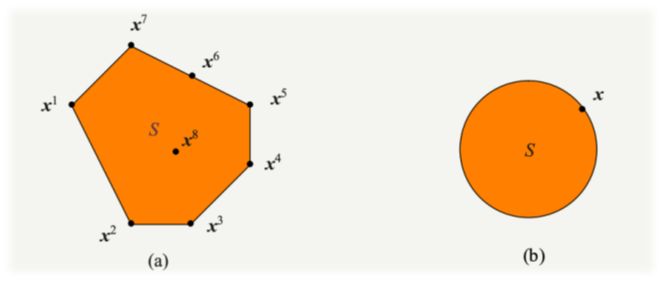
【Krein-Milman定理 】:设 S ⊆ R n S⊆\Bbb R^n S ⊆ R n 紧凸集 ,则 S = conv(ext ( S ) ) S=\text{conv(ext}(S)) S = conv(ext ( S )) ext ( S ) \text{ext}(S) ext ( S ) S S S
以图(a)为例,x 6 x_6 x 6 x 5 , x 7 x_5,x_7 x 5 , x 7 x 5 , x 7 x_5,x_7 x 5 , x 7 x 8 x_8 x 8
图(a)中的凸集S S S ext ( S ) = { x 1 , x 2 , x 3 , x 4 , x 5 , x 7 } \text{ext}(S)=\{x_1,x_2,x_3,x_4,x_5,x_7\} ext ( S ) = { x 1 , x 2 , x 3 , x 4 , x 5 , x 7 } S = conv(ext ( S ) ) S=\text{conv(ext}(S)) S = conv(ext ( S ))
Krein-Milman定理只适用于紧凸集,但对于无界集来说就不成立了。为此我们需要引出极方向的概念。
定义 设 S ⊆ R n S⊆\Bbb R^n S ⊆ R n 闭凸集 ,向量d ∈ R n , d ≠ 0 d\in\Bbb R^n,d\neq0 d ∈ R n , d = 0 ∀ x ∈ S \forall x\in S ∀ x ∈ S
{ x + λ d ∣ λ ≥ 0 } ⊂ S \{ x+\lambda d\mid\lambda\geq0\}\subset S { x + λ d ∣ λ ≥ 0 } ⊂ S
则称d d d S S S 方向 。也就是说,无论x x x S S S x x x d d d S S S d d d S S S
若d d d S S S 不同方向 的线性组合表示,则d d d S S S 极方向 。
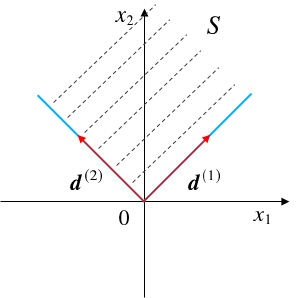
以下图为例,这是一个二维空间的多面体,其中0 0 0 d ( 1 ) , d ( 2 ) d^{(1)},d^{(2)} d ( 1 ) , d ( 2 ) d ( 1 ) , d ( 2 ) d^{(1)},d^{(2)} d ( 1 ) , d ( 2 )
更近一步对多面体进行展开,我们可以得到其表示定理 :S = { x ∣ A x = b , x ≥ 0 } S=\{x\mid Ax=b,x\geq0\} S = { x ∣ A x = b , x ≥ 0 }
ext ( S ) ≠ ∅ \text{ext}(S)\neq\varnothing ext ( S ) = ∅ 有限个极点 ;极方向集合为空的充要条件 是S S S 有限个极方向 ; x ∈ S \boldsymbol x\in S x ∈ S 充要条件 是:x = ∑ j = 1 k λ j x ( j ) + ∑ j = 1 l μ j d ( j ) ∑ j = 1 k λ j = 1 λ j ≥ 0 , j = 1 , . . . , k μ j ≥ 0 , j = 1 , . . . , l \begin{aligned} \boldsymbol x&=\sum_{j=1}^k\lambda_j\boldsymbol x^{(j)}+\sum_{j=1}^l\mu_j\boldsymbol d^{(j)}\\ &\sum_{j=1}^k\lambda_j=1\\ &\lambda_j\geq0,\quad j=1,...,k\\ &\mu_j\geq0,\quad j=1,...,l \end{aligned} x = j = 1 ∑ k λ j x ( j ) + j = 1 ∑ l μ j d ( j ) j = 1 ∑ k λ j = 1 λ j ≥ 0 , j = 1 , ... , k μ j ≥ 0 , j = 1 , ... , l
Note: 应当注意闭集 与紧集 的区别。下面补充部分集合的基础知识:
凸函数 | Convex Function 定义 设 S ⊆ R n S⊆\Bbb R^n S ⊆ R n 非空凸集 ,f f f S S S S S S x 1 , x 2 ∈ S \boldsymbol x_1,\boldsymbol x_2\in S x 1 , x 2 ∈ S ∀ λ ∈ ( 0 , 1 ) \forall\lambda\in(0,1) ∀ λ ∈ ( 0 , 1 )
f ( λ x 1 + ( 1 − λ ) x 2 ) ≤ λ f ( x 1 ) + ( 1 − λ ) f ( x 2 ) f(\lambda\boldsymbol x_1+(1-\lambda)\boldsymbol x_2)\leq\lambda f(\boldsymbol x_1)+(1-\lambda)f(\boldsymbol x_2) f ( λ x 1 + ( 1 − λ ) x 2 ) ≤ λ f ( x 1 ) + ( 1 − λ ) f ( x 2 )
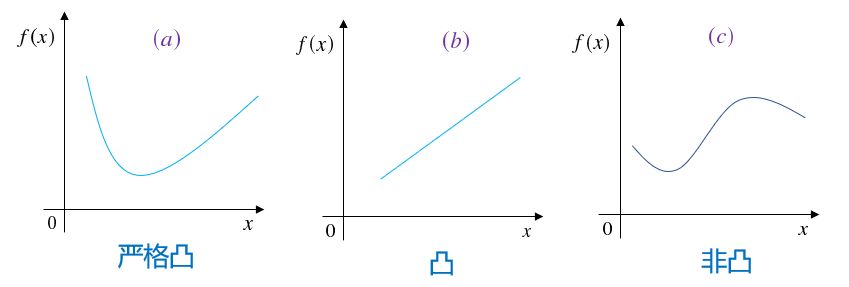
则称f f f S S S 凸函数 ,− f -f − f 偶函数 。不等号取< \lt < 严格凸函数 。
注意:在凸优化领域,甚至是数学领域提到凸函数都是上图这种形式,系从坐标数值从低往高的方向看去时的形状是凸的。与初高中乃至高等数学中学的从上往下看的定义正好相反 !
重要性质 有限个凸函数的仿射组合也是凸函数; 凸函数f : S → R f:S\to\Bbb R f : S → R 水平集 H c ( f ) = { x ∣ x ∈ S , f ( x ) ≤ c } H_c(f)=\{x|x\in S,\;f(x)\leq c\} H c ( f ) = { x ∣ x ∈ S , f ( x ) ≤ c } 凸函数f f f x 0 ∈ S x_0\in S x 0 ∈ S d d d 方向导数 D f ( x 0 ; d ) \text{D}f(x_0;d) D f ( x 0 ; d ) 凸函数f f f S S S 局部极小点就是全局极小点 (反证法可证明),极小点集合为凸集(根据性质2) 凸函数判别 【一阶条件 】当f ( x ) f(\boldsymbol x) f ( x ) S S S f f f 充要条件 为:
f ( x ( 2 ) ) ≥ f ( x ( 1 ) ) + ∇ f ( x ( 1 ) ) ⊤ ( x ( 2 ) − x ( 1 ) ) f(\boldsymbol x^{(2)})\geq f(\boldsymbol x^{(1)})+\nabla f(\boldsymbol x^{(1)})^\top(\boldsymbol x^{(2)}-\boldsymbol x^{(1)}) f ( x ( 2 ) ) ≥ f ( x ( 1 ) ) + ∇ f ( x ( 1 ) ) ⊤ ( x ( 2 ) − x ( 1 ) )
几何意义:可微函数为凸函数的充要条件是在其定义域凸集中任一点处的切平面 (切线)都不在曲面(曲线)的上方。也就是说任意点处的切线增量不超过函数的增量。
【二阶条件 】当f ( x ) f(\boldsymbol x) f ( x ) S S S f f f 充要条件 是对∀ x ∈ S \forall x\in S ∀ x ∈ S Hesse矩阵 ∇ 2 f \nabla^2f ∇ 2 f 半正定矩阵 。(是正定矩阵时则为严格凸函数)
凸优化的定义 设f ( x ) , g i ( x ) f(\boldsymbol x),g_i(\boldsymbol x) f ( x ) , g i ( x ) R n \Bbb R^n R n 凸函数 ,h j ( x ) h_j(\boldsymbol x) h j ( x ) R n \Bbb R^n R n 线性函数 ,则称最优化问题:
min f ( x ) s. t. g i ( x ) ≤ 0 , i = 1 , . . . , m h j ( x ) = 0 , j = 1 , . . . , l \begin{aligned} \min \quad&f(\boldsymbol x)\\ \text{s. t. }\quad&g_i(\boldsymbol x)\leq0,\quad i=1,...,m\\ &h_j(\boldsymbol x)=0,\quad j=1,...,l \end{aligned} min s. t. f ( x ) g i ( x ) ≤ 0 , i = 1 , ... , m h j ( x ) = 0 , j = 1 , ... , l
为凸规划。
也就是说,求凸函数在凸集上的极小点问题就是凸规划。g i ( x ) ≤ 0 g_i(\boldsymbol x)\leq0 g i ( x ) ≤ 0 h j ( x ) h_j(\boldsymbol x) h j ( x ) h j ( x ) = 0 h_j(\boldsymbol x)=0 h j ( x ) = 0
如果目标函数f ( x ) f(\boldsymbol x) f ( x ) 严格凸函数 ,且存在极小点,则其极小点唯一 。
线性规划 | Linear Programming 一般线性规划问题的标准形式 如下:
min ∑ j = 1 n c j x j s. t. ∑ j = 1 n a i j x j = b i , i = 1 , . . . , m x j ≥ 0 , j = 1 , . . . , n \begin{aligned} \min\quad&\sum_{j=1}^nc_jx_j\\ \text{s. t. }\quad&\sum_{j=1}^na_{ij}x_j=b_i,\quad i=1,...,m\\ &x_j\geq0,\quad j=1,...,n \end{aligned} min s. t. j = 1 ∑ n c j x j j = 1 ∑ n a ij x j = b i , i = 1 , ... , m x j ≥ 0 , j = 1 , ... , n
我们更常用其矩阵形式 :
min c x s. t. A x = b x ≥ 0 \begin{aligned} \min\quad&\boldsymbol{cx}\\ \text{s. t. }\quad&\boldsymbol{Ax=b}\\ &\boldsymbol{x\geq0} \end{aligned} min s. t. cx Ax = b x ≥ 0
为了计算方便,我们一般假定b ≥ 0 \boldsymbol b\geq0 b ≥ 0
形式转换 最大化 目标函数需要最大化时,对目标函数取反化为求最小值问题。
非负性 对于没有限制x ≥ 0 \boldsymbol x\geq0 x ≥ 0 x j x_j x j x j ′ , x j ′ ′ ≥ 0 x_j',x_j''\geq0 x j ′ , x j ′′ ≥ 0 x j = x j ′ − x j ′ ′ x_j=x_j'-x_j'' x j = x j ′ − x j ′′
上下界 当存在x ∈ [ a , b ] \boldsymbol x\in[a,b] x ∈ [ a , b ] x j ′ = x j − a x_j'=x_j-a x j ′ = x j − a x j ′ ≥ 0 x_j'\geq0 x j ′ ≥ 0 x j ′ ≤ b − a x_j'\leq b-a x j ′ ≤ b − a x j ′ ′ = ( b − a ) − x j ′ x_j''=(b-a)-x_j' x j ′′ = ( b − a ) − x j ′ x j ′ ′ ≥ 0 x_j''\geq0 x j ′′ ≥ 0
绝对值 在目标函数中存在∣ x j ∣ |x_j| ∣ x j ∣ x j ′ = ( x j + ∣ x j ∣ ) / 2 , x j ′ ′ = ( ∣ x j ∣ − x j ) / 2 x_j'=(x_j+|x_j|)/2,x_j''=(|x_j|-x_j)/2 x j ′ = ( x j + ∣ x j ∣ ) /2 , x j ′′ = ( ∣ x j ∣ − x j ) /2 x j = x j ′ − x j ′ ′ x_j=x_j'-x_j'' x j = x j ′ − x j ′′ ∣ x j ∣ = x j ′ + x j ′ ′ |x_j|=x_j'+x_j'' ∣ x j ∣ = x j ′ + x j ′′
不等式 当约束条件A x = b Ax=b A x = b 松弛变量 (Slack Variable)或 剩余变量 (Surplus Variable):
a 11 x 1 + ⋯ + a 1 n x n ≤ b i → a 11 x 1 + ⋯ + a 1 n x n + x n + 1 = b i \begin{aligned} a_{11}x_1+\cdots+a_{1n}x_n\leq b_i\quad\to\quad a_{11}x_1+\cdots+a_{1n}x_n+{\color{blue}{x_{n+1}}}= b_i \end{aligned} a 11 x 1 + ⋯ + a 1 n x n ≤ b i → a 11 x 1 + ⋯ + a 1 n x n + x n + 1 = b i
图解法
最优极点 显然 LP 的标准形式中,约束项是一种多面体,利用表示定理可以得到其目标函数如下:
∑ j = 1 k ( c x ( j ) ) λ j + ∑ j = 1 l ( c d ( j ) ) μ j \sum_{j=1}^k(\boldsymbol c\boldsymbol x^{(j)})\lambda_j+\sum_{j=1}^l(\boldsymbol c\boldsymbol d^{(j)})\mu_j j = 1 ∑ k ( c x ( j ) ) λ j + j = 1 ∑ l ( c d ( j ) ) μ j
并且对μ \mu μ c d ( j ) < 0 \boldsymbol c\boldsymbol d^{(j)}\lt0 c d ( j ) < 0 μ j \mu_j μ j 不存在有限最优值 。我们也称这样的问题无界 。
在此后的讨论中,我们默认这种无界情况就属于“不存在最优解”。
另外,若令c x ( p ) = min 1 ≤ j ≤ k c x ( j ) \boldsymbol c\boldsymbol x^{(p)}=\min\limits_{1\leq j\leq k}\boldsymbol c\boldsymbol x^{(j)} c x ( p ) = 1 ≤ j ≤ k min c x ( j )
c x = ∑ j = 1 k ( c x ( j ) ) λ j + ∑ j = 1 l ( c d ( j ) ) μ j ≥ ∑ j = 1 k ( c x ( j ) ) λ j ( μ j 可以都取 0 ) ≥ ∑ j = 1 k ( c x ( p ) ) λ j ( x ( j ) 可以都取 x ( p ) ) = c x ( p ) \begin{aligned} \boldsymbol c\boldsymbol x&=\sum_{j=1}^k(\boldsymbol c\boldsymbol x^{(j)})\lambda_j+\sum_{j=1}^l(\boldsymbol c\boldsymbol d^{(j)})\mu_j\\ &\geq\sum_{j=1}^k(\boldsymbol c\boldsymbol x^{(j)})\lambda_j\qquad(\text{$\mu_j可以都取0$})\\ &\geq\sum_{j=1}^k(\boldsymbol c\boldsymbol x^{(p)})\lambda_j\qquad(\text{$x^{(j)}可以都取x^{(p)}$})\\ &=\boldsymbol c\boldsymbol x^{(p)} \end{aligned} c x = j = 1 ∑ k ( c x ( j ) ) λ j + j = 1 ∑ l ( c d ( j ) ) μ j ≥ j = 1 ∑ k ( c x ( j ) ) λ j ( μ j 可以都取 0 ) ≥ j = 1 ∑ k ( c x ( p ) ) λ j ( x ( j ) 可以都取 x ( p ) ) = c x ( p )
从而说明目标函数的最小值可以在某个极点上取到。
以上两方面的推导告诉我们,如果c d ( j ) < 0 \boldsymbol c\boldsymbol d^{(j)}\lt 0 c d ( j ) < 0
🔔最优基本可行解 在 LP 模型中,我们将系数矩阵A ∈ R m × n A\in\Bbb R^{m\times n} A ∈ R m × n A = ( p 1 , p 2 , . . . , p n ) , p i ∈ R m A=(p_1,p_2,...,p_n),\;p_i\in\Bbb R^m A = ( p 1 , p 2 , ... , p n ) , p i ∈ R m
A x = b ⇒ p 1 x 1 + p 2 x 2 + ⋯ + p n x n = b Ax=b\Rightarrow p_1x_1+p_2x_2+\cdots+p_nx_n=b A x = b ⇒ p 1 x 1 + p 2 x 2 + ⋯ + p n x n = b
又假设r ( A ) = m r(A)=m r ( A ) = m A A A m m m p i p_i p i m m m 满秩 方阵,记为B B B 有限次列变换 ,有A = [ B , N ] A=[B,N] A = [ B , N ] x = [ x B , x N ] x=[x_B,x_N] x = [ x B , x N ]
( B N ) ( x B x N ) = b ⇔ B x B + N x N = b ⇒ x B = B − 1 b − B − 1 N x N \begin{aligned} &\begin{pmatrix}B&N\end{pmatrix}\begin{pmatrix}x_B\\x_N\end{pmatrix}=b\\ \Leftrightarrow\quad& Bx_B+Nx_N=b\\ \Rightarrow\quad& x_B=B^{-1}b-B^{-1}Nx_N \end{aligned} ⇔ ⇒ ( B N ) ( x B x N ) = b B x B + N x N = b x B = B − 1 b − B − 1 N x N
而x N x_N x N 自由未知量 ,它们取不同的值就能得到方程组不同的解。
特别地,我们都取为零,得到的x x x A x = b Ax=b A x = b 基本解 :
x = ( x B x N ) = ( B − 1 b 0 ) x=\begin{pmatrix}x_B\\x_N\end{pmatrix}=\begin{pmatrix}B^{-1}b\\0\end{pmatrix} x = ( x B x N ) = ( B − 1 b 0 )
其中,B B B 基矩阵 ,简称为基 ,x B x_B x B 基变量 。
如果基本解满足非负约束,即B − 1 b ≥ 0 B^{-1}b\geq0 B − 1 b ≥ 0 基本可行解 。B − 1 b B^{-1}b B − 1 b 0 0 0 退化的 ;B − 1 b > 0 B^{-1}b\gt0 B − 1 b > 0 非退化的 。
不难发现,基本解的个数与基矩阵的个数一致,而基矩阵的个数等价于每次从n n n m m m
C n m = n ! m ! ( n − m ) ! C_n^m=\frac{n!}{m!(n-m)!} C n m = m ! ( n − m )! n !
此外还可以证明,可行域 K = { x ∣ A x = b , x ≥ 0 } K=\{x\mid Ax=b,\;x\geq0\} K = { x ∣ A x = b , x ≥ 0 } ext ( K ) \text{ext}(K) ext ( K ) 基本可行解 等价。而在上一节我们指出如果LP存在最优解,那么一定能在某个极点上取得。
于是,LP问题的求解就相当于求最优基本可行解 。
单纯形法 | Simplex Method 上一章节我们已经论述了LP问题的求解等价于求最优基本可行解 。我们能想到的一个最简单的求解方法就是将所有可能的基本可行解一一枚举,然后哪一个解使得目标函数值最小(标准形式的目标函数是最小化的),那么那个解就是最优解。
显然这个方法在变量过大时,计算是低效的(并且还要反复计算逆矩阵 )。于是,单纯形法 就提出了这样的思想:一些改动 ,使得目标函数值比之前更优 ;如此下去,直到找到最优解为止。
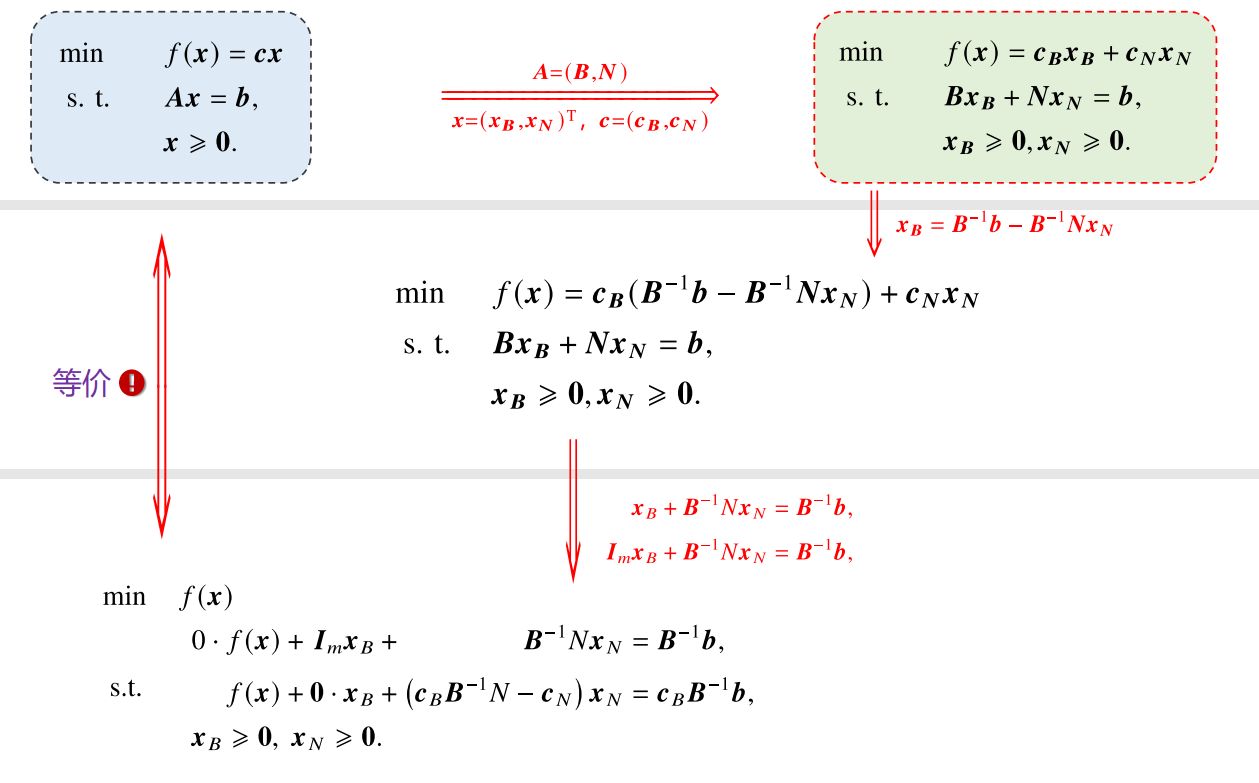
最优解判别准则 为了推理更加清晰,我们下面都使用标准LP的矩阵形式,并且沿用上一章对基本可行解的等价形式转换,如下图所示。
假设我们目前得到了一个基本可行解:
x ( 0 ) = [ B − 1 b 0 ] \boldsymbol x^{(0)}=\begin{bmatrix}B^{-1}\bf b\\\bf0\end{bmatrix} x ( 0 ) = [ B − 1 b 0 ]
此时的目标函数值:
f 0 = c x ( 0 ) = c B B − 1 b f_0=\boldsymbol{cx}^{(0)}=\boldsymbol c_BB^{-1}\boldsymbol b f 0 = cx ( 0 ) = c B B − 1 b
又设任意一个基本可行解:
x = [ x B x N ] \boldsymbol x=\begin{bmatrix}\boldsymbol x_B\\\boldsymbol x_N\end{bmatrix} x = [ x B x N ]
由A x = b A\boldsymbol x=\boldsymbol b A x = b
x B = B − 1 b − B − 1 N x N \boldsymbol x_B=B^{-1}\boldsymbol b-B^{-1}N\boldsymbol x_N x B = B − 1 b − B − 1 N x N
从而在x \boldsymbol x x
f = c x = c B x B + c N x N = c B ( B − 1 b − B − 1 N x N ) + c N x N = c B B − 1 b − ( c B B − 1 N − c N ) x N = f 0 − ( c B B − 1 N − c N ) x N / / ∵ f 0 = c B B − 1 b = f 0 − ∑ j ∈ R ( c B B − 1 p j − c j ) x j / / R 为非基变量的下标集合 = f 0 − ∑ j ∈ R ( z j − c j ) x j \begin{aligned} f&=\boldsymbol {cx}=\boldsymbol c_B\boldsymbol x_B+\boldsymbol c_N\boldsymbol x_N\\ &=\boldsymbol c_B(B^{-1}\boldsymbol b-B^{-1}N\boldsymbol x_N)+\boldsymbol c_N\boldsymbol x_N\\ &=\boldsymbol c_BB^{-1}\boldsymbol b -(\boldsymbol c_BB^{-1}N-\boldsymbol c_N)\boldsymbol x_N\\ &=f_0-(\boldsymbol c_BB^{-1}N-\boldsymbol c_N)\boldsymbol x_N\quad//\because f_0=\boldsymbol c_BB^{-1}\boldsymbol b\\ &=f_0-\sum_{j\in R}(\boldsymbol c_BB^{-1}\boldsymbol p_j-c_j)x_j\quad//R\text{ 为非基变量的下标集合}\\ &=f_0-\sum_{j\in R}(z_j-c_j)x_j \end{aligned} f = cx = c B x B + c N x N = c B ( B − 1 b − B − 1 N x N ) + c N x N = c B B − 1 b − ( c B B − 1 N − c N ) x N = f 0 − ( c B B − 1 N − c N ) x N // ∵ f 0 = c B B − 1 b = f 0 − j ∈ R ∑ ( c B B − 1 p j − c j ) x j // R 为非基变量的下标集合 = f 0 − j ∈ R ∑ ( z j − c j ) x j
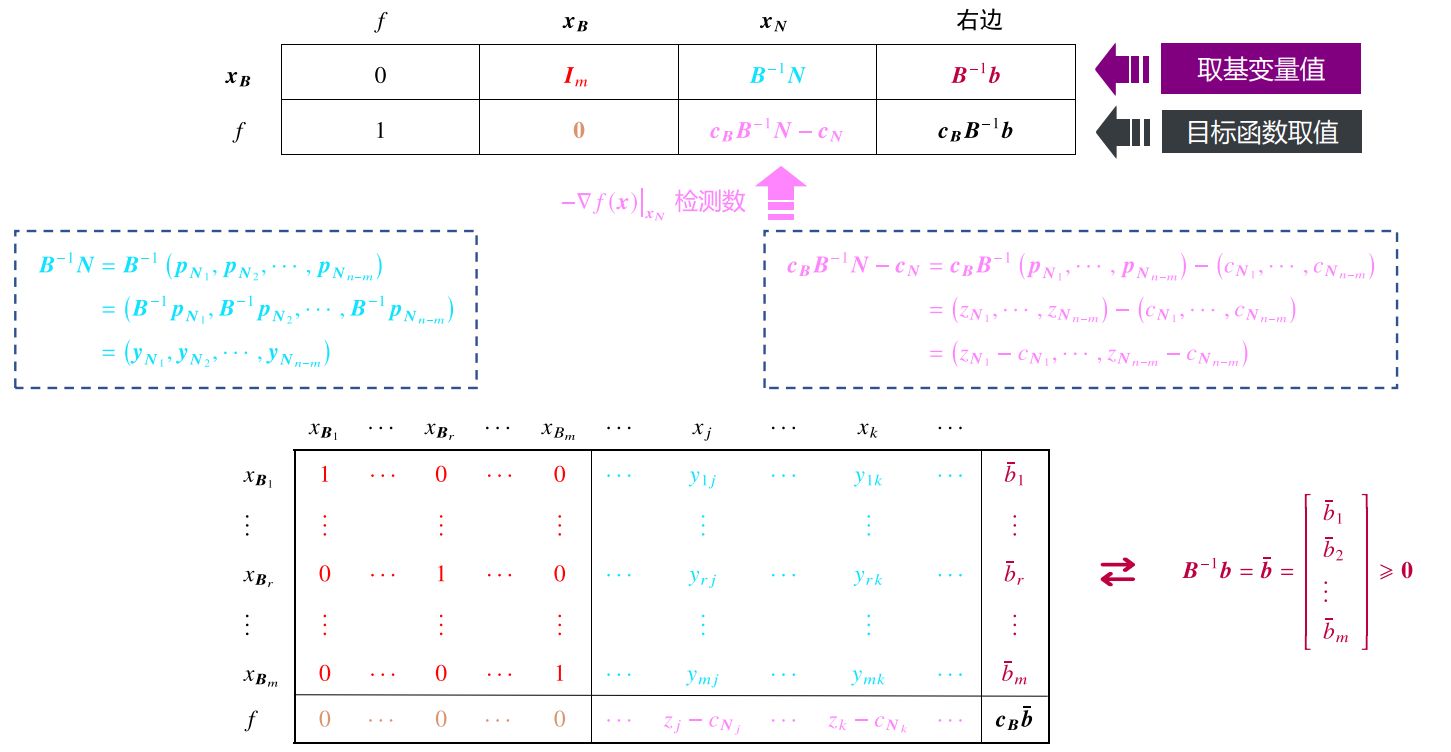
其中,定义c B B − 1 p j = z j \boldsymbol c_BB^{-1}\boldsymbol p_j=z_j c B B − 1 p j = z j x j x_j x j
∑ j ∈ R ( z j − c j ) x j > 0 \sum_{j\in R}(z_j-c_j)x_j\gt0 j ∈ R ∑ ( z j − c j ) x j > 0
那么,目标函数值就能得到改善。
由于非基变量也需要满足x N ≥ 0 \boldsymbol x_N\geq\boldsymbol 0 x N ≥ 0 z j − c j > 0 z_j-c_j\gt0 z j − c j > 0
所以,我们称z j − c j z_j-c_j z j − c j 判别数 或检验数 。
事实上,目标函数对非基变量的梯度∇ f ( x ) ∣ x N = − ( z 1 − c 1 , . . . , z k − c k , . . . ) T \nabla f(\boldsymbol x)|_{\boldsymbol x_N}=-(z_1-c_1,...,z_k-c_k,...)^T ∇ f ( x ) ∣ x N = − ( z 1 − c 1 , ... , z k − c k , ... ) T
进基变量的选择 考虑还没有到达最优解的情况,即∃ j ∈ R \exists j\in R ∃ j ∈ R z j − c j > 0 z_j-c_j\gt0 z j − c j > 0
max x N ∑ j ∈ R ( z j − c j ) x j \max_{\boldsymbol x_N}\sum_{j\in R}(z_j-c_j)x_j x N max j ∈ R ∑ ( z j − c j ) x j
在调整基本可行解时,单纯形法的思想是“逐步”调整的。也就是从非基变量中选取一个变量,将其划归到基变量内,称为进基 ,选一个基变量中的变量划归到非基变量内,称为离基 。所以这里不失一般性地,我们令n − m n-m n − m x k x_k x k 进基变量 。
在这样的情况下,就有:
max x N ∑ j ∈ R ( z j − c j ) x j = ( z k − c k ) x k where k = arg max j ∈ R ( z j − c j ) \max_{\boldsymbol x_N}\sum_{j\in R}(z_j-c_j)x_j=(z_k-c_k)x_k\quad\text{where }k=\arg\max_{j\in R}(z_j-c_j) x N max j ∈ R ∑ ( z j − c j ) x j = ( z k − c k ) x k where k = arg j ∈ R max ( z j − c j )
因为x k x_k x k z k − c k z_k-c_k z k − c k x k x_k x k f f f x k x_k x k x B = B − 1 b − B − 1 N x N \boldsymbol x_B=B^{-1}\boldsymbol b-B^{-1}N\boldsymbol x_N x B = B − 1 b − B − 1 N x N x B = B − 1 b − B − 1 p k x k : = b ˉ − y k x k \boldsymbol x_B=B^{-1}\boldsymbol b-B^{-1}\boldsymbol p_kx_k:=\bar{\boldsymbol b}-\boldsymbol y_kx_k x B = B − 1 b − B − 1 p k x k := b ˉ − y k x k x B ≥ 0 \boldsymbol x_B\geq \boldsymbol 0 x B ≥ 0
首先,B − 1 b = b ˉ ≥ 0 B^{-1}\boldsymbol b=\bar{\boldsymbol b}\geq\boldsymbol 0 B − 1 b = b ˉ ≥ 0 x ( 0 ) \boldsymbol x^{(0)} x ( 0 ) y k ≤ 0 \boldsymbol y_k\leq\boldsymbol 0 y k ≤ 0 x B \boldsymbol x_B x B x k x_k x k 原问题无界 了。
接下来我们进一步考虑y k ≰ 0 \boldsymbol y_k\not\leq\boldsymbol 0 y k ≤ 0 x B ≥ 0 \boldsymbol x_B\geq \boldsymbol 0 x B ≥ 0 x k x_k x k
∀ i , x k ≤ b ˉ i y i k \forall i,\quad x_k\leq\frac{\bar b_i}{y_{ik}} ∀ i , x k ≤ y ik b ˉ i
其中,i i i
当然我们希望尽可能选最大的x k x_k x k
x k = min i { b ˉ i y i k ∣ y i k > 0 } = b ˉ r y r k x_k=\min_i\left\{\frac{\bar{b}_i}{y_{ik}}\bigg|y_{ik}\gt0\right\}=\frac{\bar{b}_r}{y_{rk}} x k = i min { y ik b ˉ i y ik > 0 } = y r k b ˉ r
离基变量的选择 基变量中的x r x_r x r r r r x k = b ˉ r / y r k x_k=\bar{b}_r/y_{rk} x k = b ˉ r / y r k
p k \boldsymbol p_k p k N N N k k k y k = B − 1 p k \boldsymbol y_k=B^{-1}\boldsymbol p_k y k = B − 1 p k
p k = B y k = ∑ i = 1 m y i k p B i \boldsymbol p_k=B\boldsymbol y_k=\sum_{i=1}^my_{ik}\boldsymbol p_{B_i} p k = B y k = i = 1 ∑ m y ik p B i
它是基矩阵B B B m m m p B i \boldsymbol p_{B_i} p B i 线性组合 。m m m B B B p B r \boldsymbol p_{B_r} p B r p k \boldsymbol p_k p k 依然线性无关 。所以新的基本解x \boldsymbol x x
替换得到新的可行解后,在不进行新的调整时(取新的x N = 0 \boldsymbol x_N=\boldsymbol 0 x N = 0
f = c B x B = f 0 − c B r x r + c k x k f=\boldsymbol c_B\boldsymbol x_B=f_0-c_{B_r }x_r+c_kx_k f = c B x B = f 0 − c B r x r + c k x k
而z k = c B r ⋅ y r k , x k = b ˉ r / y r k = x r / y r k z_k=c_{B_r}·y_{rk},\;x_k=\bar{b}_r/y_{rk}=x_r/y_{rk} z k = c B r ⋅ y r k , x k = b ˉ r / y r k = x r / y r k f = f 0 − ( z k − c k ) x k f=f_0-(z_k-c_k)x_k f = f 0 − ( z k − c k ) x k ( z k − c k ) x k (z_k-c_k)x_k ( z k − c k ) x k
🔔算法流程 综合以上论述,我们得到单纯形法的一般算法流程:
单纯形表 | 表格法 用单纯形法求解LP的过程,其实就是一个解线性方程组的过程。只是在求解过程中需要按照某种规则挑选自由未知量,但是其他变换过程就是简单的行变换 。所以,我们可以通过预先的某种变化,将单纯形法计算过程中需要用到的变量(如z j , c j , y i k z_j,c_j,y_{ik} z j , c j , y ik
下面我们在以前对原问题的转换中进一步修改,进行等价 转换:
此时,整个约束条件就是一个关于f ( x ) , x B f(\boldsymbol x),\boldsymbol x_B f ( x ) , x B x N \boldsymbol x_N x N 增广矩阵 :
快速填充方法 在实际利用表格法时,我们可以不用像上图那样严格按照基变量和非基变量的顺序填表。特别地,当选取的初始基矩阵B B B m m m I m I_m I m
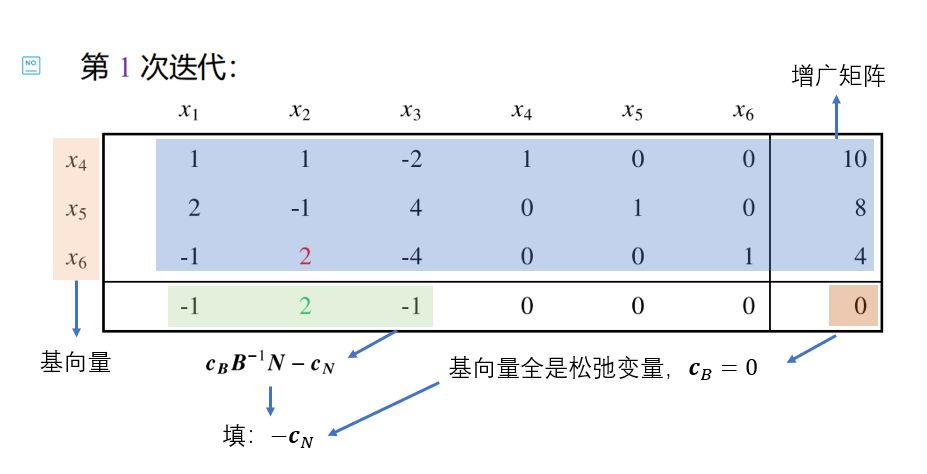
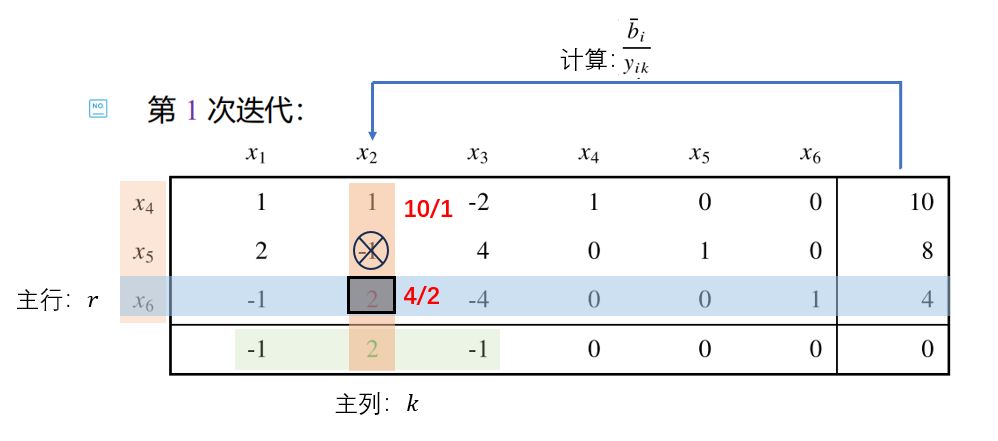
填充约束A x = b A\boldsymbol x=\boldsymbol b A x = b [ A , b ] [A,b] [ A , b ] 将A A A m m m 基变量 ,按照 1 出现的次序依次填在最左边(表格外最左边一列的索引); 基变量对应的列,最后一行都填 0,非基变量 计算c B y j − c j \boldsymbol {c_By_j}-c_j c B y j − c j 计算初始目标函数值f 0 = c B b ˉ f_0=\boldsymbol c_B\bar{\boldsymbol b} f 0 = c B b ˉ c B = 0 \boldsymbol c_B=\mathbf 0 c B = 0 f 0 = 0 f_0=0 f 0 = 0 以下面这个问题为例,我们给出一个快速填表的示例:
基本判别规则 填完表之后,因为最后一行是[判别数, 0, 目标函数值]。所以,
第一步 :看是不是所有判别数都小于等于0,如果是,说明已经得到最优解 。否则,第二步 :找到判别数最大 (z k − c k z_k-c_k z k − c k 主列 。第三步 :查看主列的除最后一行外的所有值(其实就是y i k y_{ik} y ik 问题无界 。否则,第四步 :验证最后一列的值(其实就是b ˉ i \bar{b}_i b ˉ i y i k > 0 y_{ik}\gt0 y ik > 0 r r r 主行 。
仍然以上面那么例子做演示,上面的四步可以可视化如下图:
主元消去法 由主行和主列得到的元素我们称为主元 。x k x_k x k x r x_r x r
整个可行解的调整过程很简单,就是利用主元消去法 :对单纯形表作有限次行变换使得主元所在的位置调整为 1,主列其他位置为 0。
最后表格外最左边的基变量对应位置替换成x k x_k x k
为什么主元消去法正好对应进基和离基过程呢?1 ,主列其他位置为 0。不考虑最后一行时,相当于线性方程组的等价变换,所以不改变问题。
接下来我们来思考主元消去法对最后一行的影响:
要使主元位置为 1,需要将第r r r y r k y_{rk} y r k 0,需要在前面的基础上将最后一行减去第r r r z k − z c z_k-z_c z k − z c 从而,非主列的其他最后一行的元素就变为:
( z j − c j ) ′ = ( z j − c j ) − ( y r j / y r k ) ( z k − c k ) (z_j-c_j)'=(z_j-c_j)-(y_{rj}/y_{rk})(z_k-c_k) ( z j − c j ) ′ = ( z j − c j ) − ( y r j / y r k ) ( z k − c k )
这是新的判别数 。
( c B B − 1 b ) ′ = c B B − 1 b − ( b ˉ r / y r k ) ( z k − c k ) (\boldsymbol c_BB^{-1}\boldsymbol b)'=\boldsymbol c_BB^{-1}\boldsymbol b-(\bar{b}_r/y_{rk})(z_k-c_k) ( c B B − 1 b ) ′ = c B B − 1 b − ( b ˉ r / y r k ) ( z k − c k )
这就是下降后的新目标函数值 。
此时,最后一列(不含最后一个)的值b ˉ = x B \bar{\boldsymbol b}=\boldsymbol x_B b ˉ = x B
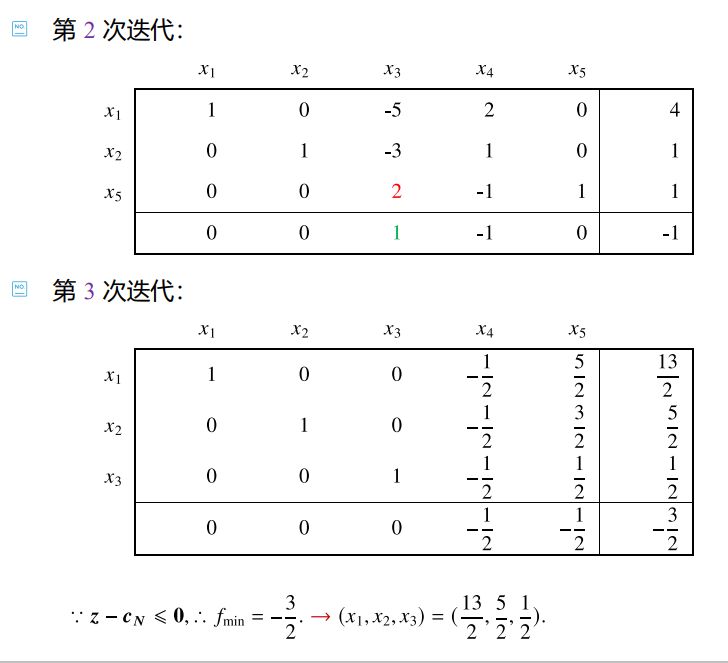
如此往复进行迭代 ,直到满足最优解条件时,整个单纯形表的最后一列就对应了最优解和目标函数最优值。
根据新的判别数 和新的目标函数值 的更新公式,我们可以看出,当存在判别数z j − c j = 0 z_j-c_j=0 z j − c j = 0 x j x_j x j
新判别数小于0时,它以后不会再被考虑加入基变量; 新判别数等于0时,等到它被视为进基变量(因为只要还有判别数不小于0,就说明目标函数还有下降的可能,算法会继续找进基变量),此时新的目标函数值不会再变化。 从而我们可以得出一个结论:当∃ j ∈ R , − ∇ f ( x ) ∣ x N j = 0 \exists j\in R,-\nabla f(\boldsymbol x)|_{\boldsymbol x_{N_j}}=0 ∃ j ∈ R , − ∇ f ( x ) ∣ x N j = 0 LP有多个解 (但不是无限个)。
上面那个例子的几次迭代与最终结果如下:
引入人工变量 前面我们介绍快速填充时,有一个强假设 :系数矩阵中可以直接找出满秩单位矩阵I m I_m I m A x = b A\boldsymbol x=\boldsymbol b A x = b 但现实中不一定能够这么幸运和容易的 。
为了解决这个问题,我们可以人为引入变量x α \boldsymbol x_\alpha x α 强行存在单位阵 。这种变量被称为人工变量 。引入方法如下:
与松弛变量不同,人工变量的引入会改变原来的约束! 可以说它是一种“不合法”的变量。所以引入它之后,我们希望调整新的基本可行解使得在这个解下面x α = 0 \boldsymbol x_\alpha=\boldsymbol 0 x α = 0 A x + x α = A x = b A\boldsymbol x+\boldsymbol x_\alpha=A\boldsymbol x=\boldsymbol b A x + x α = A x = b
🔔两阶段法 两阶段法提出,在求解LP的第一阶段 ,先用单纯形法求解一个辅助LP:
min e T x α s. t. A x + x α = b x ≥ 0 , x α ≥ 0 \begin{aligned} \min\quad&\boldsymbol{e^Tx}_\alpha\\ \text{s. t. }\quad&\boldsymbol{Ax+x_\alpha=b}\\ &\boldsymbol{x\geq0,x_\alpha\geq0} \end{aligned} min s. t. e T x α Ax + x α = b x ≥ 0 , x α ≥ 0
其中,e = ( 1 , 1 , . . . , 1 ) T \boldsymbol e=(1,1,...,1)^T e = ( 1 , 1 , ... , 1 ) T m m m
显然,由于x α ≥ 0 \boldsymbol x_\alpha\geq0 x α ≥ 0 e T x α ≥ 0 \boldsymbol e^T\boldsymbol x_\alpha\geq0 e T x α ≥ 0 x α = 0 \boldsymbol x_\alpha=\boldsymbol 0 x α = 0 x α = 0 \boldsymbol x_\alpha=\boldsymbol 0 x α = 0
假如求解这个辅助LP得到最优基本可行解( x ‾ ⊤ , x ‾ α ⊤ ) (\overline{\boldsymbol x}^\top,\overline{\boldsymbol x}^\top_\alpha) ( x ⊤ , x α ⊤ )
x ‾ α ≠ 0 \overline{\boldsymbol x}_\alpha\neq\bf0 x α = 0 x ‾ α = 0 \overline{\boldsymbol x}_\alpha=\bf0 x α = 0 x ‾ \overline{\boldsymbol x} x x ‾ α = 0 \overline{\boldsymbol x}_\alpha=\bf0 x α = 0 Note:第三种情况提到的主元消去法与表格法略有不同,可以不遵循单纯形法限定的离基和进基规则,我们的目的主要是希望把人工变量转换成非基变量,从而得到原始LP的只与x \boldsymbol x x
当一阶段得到基本可行解之后,两阶段法的第二阶段 就和单纯形法一样了。并且在一阶段时留下的单纯形表还可以继续使用(需要把最后一行的判别数与函数值按照原始LP的目标函数进行修正 )。
🔔大M法 大M M M M M M c x + M e T x α \boldsymbol{cx}+M\boldsymbol{e^Tx}_\alpha cx + M e T x α
当M M M e T x α = 0 \boldsymbol{e^Tx}_\alpha=\bf0 e T x α = 0 c x \boldsymbol{cx} cx
但是和两阶段法一样,求解这个新LP可能存在下列几种情况:
得到最优解( x ‾ ⊤ , x ‾ α ⊤ ) (\overline{\boldsymbol x}^\top,\overline{\boldsymbol x}^\top_\alpha) ( x ⊤ , x α ⊤ ) x ‾ α = 0 \overline{\boldsymbol x}_\alpha=\bf0 x α = 0 x ‾ \overline{\boldsymbol x} x 得到最优解( x ‾ ⊤ , x ‾ α ⊤ ) (\overline{\boldsymbol x}^\top,\overline{\boldsymbol x}^\top_\alpha) ( x ⊤ , x α ⊤ ) e T x α > 0 \boldsymbol{e^Tx}_\alpha\gt0 e T x α > 0 新LP无界/不存在有限最优值,且x ‾ α = 0 \overline{\boldsymbol x}_\alpha=\bf0 x α = 0 新LP无界/不存在有限最优值,但e T x α > 0 \boldsymbol{e^Tx}_\alpha\gt0 e T x α > 0 单个人工变量技巧 之前我们探讨了我们为了保险起见——找到基本可行解,引入了m m m
首先我们同样将系数矩阵A A A [ B , N ] [B,N] [ B , N ] B B B 满秩 的,不需要 选出来的变量一定是可行的基变量。首先同样有:
B x B + N x N = b B\boldsymbol x_B+N\boldsymbol x_N=\boldsymbol b B x B + N x N = b
两边同时左乘B − 1 B^{-1} B − 1 b ˉ = B − 1 b \bar{\boldsymbol b}=B^{-1}\boldsymbol b b ˉ = B − 1 b
x B + B − 1 N x N = b ˉ \boldsymbol x_B+B^{-1}N\boldsymbol x_N=\bar{\boldsymbol b} x B + B − 1 N x N = b ˉ
取N N N x N = 0 \boldsymbol x_N=\bf0 x N = 0 x = [ x B x N ] = [ b ˉ 0 ] \boldsymbol x=\begin{bmatrix}\boldsymbol x_B\\\boldsymbol x_N\end{bmatrix}=\begin{bmatrix}\bar{\boldsymbol b}\\\bf0\end{bmatrix} x = [ x B x N ] = [ b ˉ 0 ]
当然,我们需要让这个解满足非负约束x ≥ 0 \boldsymbol x\geq\bf0 x ≥ 0 b ˉ ≥ 0 \bar{\boldsymbol b}\geq\bf0 b ˉ ≥ 0
通常我们不是先找任意一个B B B b ˉ ≥ 0 ? \bar{\boldsymbol b}\geq\bf0? b ˉ ≥ 0 ? I m I_m I m
不过现在我们更想关注b ˉ ≱ 0 \bar{\boldsymbol b}\not\geq\bf0 b ˉ ≥ 0
我们引入一个人工变量x a ≥ 0 x_a\geq0 x a ≥ 0
x B + B − 1 N x N − x a e = b ˉ \boldsymbol x_B+B^{-1}N\boldsymbol x_N-x_a\boldsymbol e=\bar{\boldsymbol b} x B + B − 1 N x N − x a e = b ˉ
记b ˉ = ( b ˉ 1 , . . . , b ˉ m ) T \bar{\boldsymbol b}=(\bar{b}_1,...,\bar{b}_m)^T b ˉ = ( b ˉ 1 , ... , b ˉ m ) T b ˉ ≥ 0 \bar{\boldsymbol b}\geq0 b ˉ ≥ 0 b ˉ \bar{\boldsymbol b} b ˉ
b ˉ r = min i = 1 , . . , m { b ˉ i } < 0 \bar{b}_r=\min_{i=1,..,m}\{\bar{b}_i\}\lt0 b ˉ r = i = 1 , .. , m min { b ˉ i } < 0
从而以第r r r 主行 ,x a x_a x a 主列 ,通过主元消去法把x a x_a x a b ˉ \bar{\boldsymbol b} b ˉ M M M
退化情形与摄动法 待更
修正单纯形法 | Correctional Simplex Method 待更
LP的对偶理论 每一个LP都存在另一个与它密切相关的LP,我们称其中之一为原问题,另一个称为它的对偶问题 。它们之间的内在联系为进一步深入研究LP的理论与算法提供了理论依据。
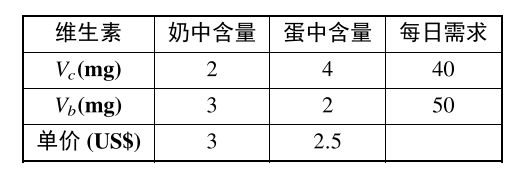
下面我们以最经典的食谱问题切入:
对于“卖家 ”[注1] 来说,他希望对维生素V c , V b V_c,V_b V c , V b x , y x,y x , y
对于“买家 ”来说,他希望能购买m m m n n n
于是,从他们二者的角度出发,我们可以写出两个线性规划[注2] :
注1:这里所谓的“卖家”,是指“卖维生素的商家”,与奶和蛋的商家是竞争关系。最优目标函数值相等 。
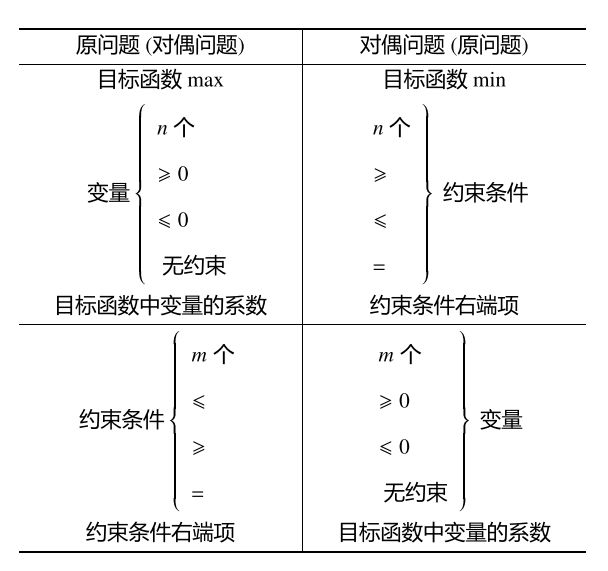
对偶问题的转换 线性规划中的对偶可以概括为三种形式。
对称形式的对偶 原问题
min c x s. t. A x ≥ b x ≥ 0 \begin{aligned} \min\quad&\boldsymbol{cx}\\ \text{s. t. }\quad&\boldsymbol{Ax\geq b}\\ &\boldsymbol{x\geq0} \end{aligned} min s. t. cx Ax ≥ b x ≥ 0
对偶问题
max w b s. t. w A ≤ c w ≥ 0 \begin{aligned} \max\quad&\boldsymbol{wb}\\ \text{s. t. }\quad&\boldsymbol{wA\leq c}\\ &\boldsymbol{w\geq0} \end{aligned} max s. t. wb wA ≤ c w ≥ 0
其中,A ∈ R m × n \boldsymbol A\in\Bbb R^{m\times n} A ∈ R m × n w \boldsymbol{w} w m m m x \boldsymbol x x
可以证明:对偶问题的对偶为原问题 .
非对称形式的对偶 考虑具有等式约束的LP:
min c x s. t. A x = b x ≥ 0 \begin{aligned} \min\quad&\boldsymbol{cx}\\ \text{s. t. }\quad&\boldsymbol{Ax=b}\\ &\boldsymbol{x\geq0} \end{aligned} min s. t. cx Ax = b x ≥ 0
可以将其利用不等式规则:( x ≥ a ) ∧ ( x ≤ a ) → x = a (x\geq a)\land(x\leq a)\to x=a ( x ≥ a ) ∧ ( x ≤ a ) → x = a
min c x s. t. A x ≥ b − A x ≥ − b x ≥ 0 \begin{aligned} \min\quad&\boldsymbol{cx}\\ \text{s. t. }\quad&\boldsymbol{Ax\geq b}\\ &\boldsymbol{-Ax\geq -b}\\ &\boldsymbol{x\geq0} \end{aligned} min s. t. cx Ax ≥ b − Ax ≥ − b x ≥ 0
从而其对偶问题可以写作:
min u b − v b s. t. u A − v A ≤ c u , v ≥ 0 \begin{aligned} \min\quad&\boldsymbol{ub-vb}\\ \text{s. t. }\quad&\boldsymbol{uA-vA\leq c}\\ &\boldsymbol{u,v\geq0} \end{aligned} min s. t. ub − vb uA − vA ≤ c u , v ≥ 0
令w = u − v \boldsymbol{w=u-v} w = u − v
min w b s. t. w A ≤ c \begin{aligned} \min\quad&\boldsymbol{wb}\\ \text{s. t. }\quad&\boldsymbol{wA\leq c} \end{aligned} min s. t. wb wA ≤ c
此时,w \boldsymbol w w 无非负约束 !
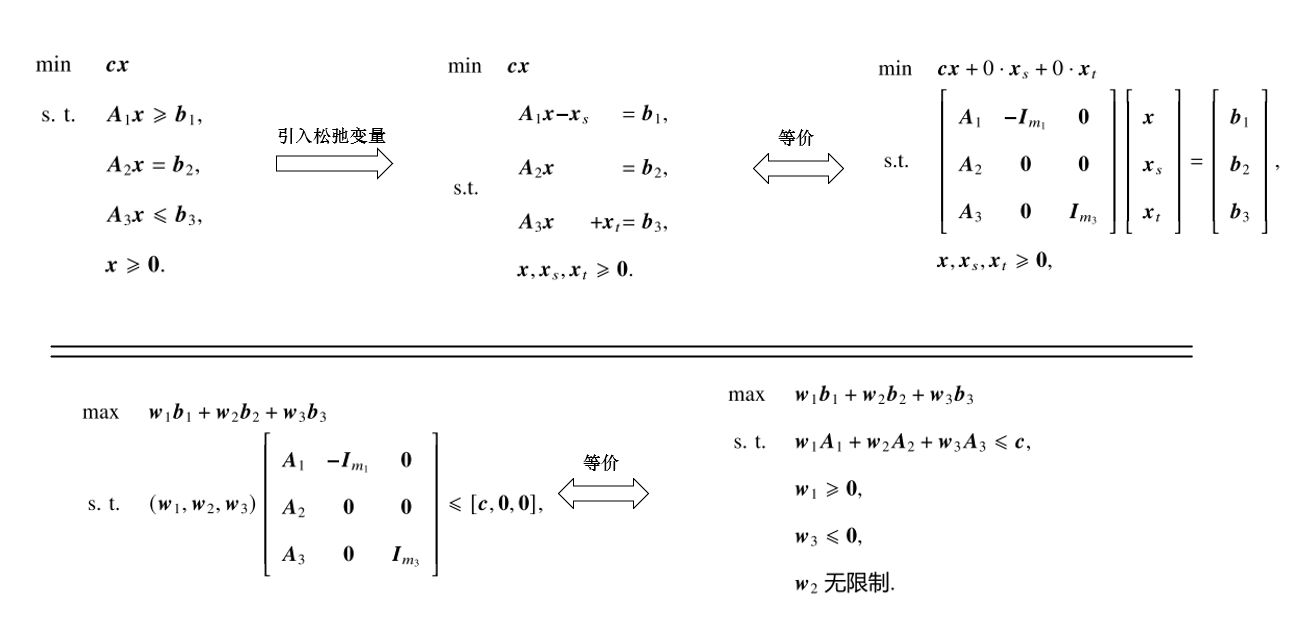
一般情形下的对偶 当原问题约束存在多种不等式约束时,我们可以引入松弛变量x s , x t \boldsymbol x_s,\boldsymbol x_t x s , x t 非对称形式的对偶 。整个推导过程如下:
经过这样的推导,我们还可以总结出以下规律,便于我们以后快速得出对偶问题:
对偶定理及其推论 下面研究对偶的基本性质. 此处仅叙述对称形式的对偶 ,但对其他形式仍是成立的.
定理 设x ( 0 ) , w ( 0 ) \boldsymbol x^{(0)},\boldsymbol w^{(0)} x ( 0 ) , w ( 0 ) ( L ) (L) ( L ) ( D ) (D) ( D ) c x ( 0 ) ≥ w ( 0 ) b \boldsymbol{cx}^{(0)}\geq\boldsymbol w^{(0)}\boldsymbol b cx ( 0 ) ≥ w ( 0 ) b
证明 这个定理指出,极小化问题给出了极大化问题的目标函数上界;极大化问题给出了极小化问题的目标函数下界。对应的,如果对偶问题无上/下界则说明原问题无可行解。
根据该定理还可以得出以下推论 :
若x ( 0 ) , w ( 0 ) \boldsymbol x^{(0)},\boldsymbol w^{(0)} x ( 0 ) , w ( 0 ) ( L ) (L) ( L ) ( D ) (D) ( D ) c x ( 0 ) = w ( 0 ) b \boldsymbol{cx}^{(0)}=\boldsymbol w^{(0)}\boldsymbol b cx ( 0 ) = w ( 0 ) b 最优解 ; ( L ) (L) ( L ) ( D ) (D) ( D ) 充要条件 是它们同时有可行解。定理 若原问题( L ) (L) ( L ) ( D ) (D) ( D )
证明
推论 :若( L ) (L) ( L ) B B B w = c B B − 1 \boldsymbol w=\boldsymbol c_BB^{-1} w = c B B − 1 ( D ) (D) ( D ) 互补松弛性质 设x ( 0 ) , w ( 0 ) \boldsymbol x^{(0)},\boldsymbol w^{(0)} x ( 0 ) , w ( 0 ) ( L ) (L) ( L ) ( D ) (D) ( D ) x ( 0 ) , w ( 0 ) \boldsymbol x^{(0)},\boldsymbol w^{(0)} x ( 0 ) , w ( 0 ) ∀ i , j 1 ≤ i ≤ m ; 1 ≤ j ≤ n \forall i,j\quad 1\leq i\leq m;\;1\leq j\leq n ∀ i , j 1 ≤ i ≤ m ; 1 ≤ j ≤ n
如果x j ( 0 ) > 0 x_j^{(0)}\gt0 x j ( 0 ) > 0 w ( 0 ) p j = c j \boldsymbol w^{(0)}\boldsymbol p_j=c_j w ( 0 ) p j = c j 如果w ( 0 ) p j < c j \boldsymbol w^{(0)}\boldsymbol p_j\lt c_j w ( 0 ) p j < c j x j ( 0 ) = 0 x_j^{(0)}=0 x j ( 0 ) = 0 如果w i ( 0 ) > 0 w_i^{(0)}\gt0 w i ( 0 ) > 0 A i x ( 0 ) = b i \boldsymbol A_i\boldsymbol x^{(0)}=b_i A i x ( 0 ) = b i 如果A i x ( 0 ) > b i \boldsymbol A_i\boldsymbol x^{(0)}\gt b_i A i x ( 0 ) > b i w i ( 0 ) = 0 w_i^{(0)}=0 w i ( 0 ) = 0 对于非对称形式,则满足前两条即可。
这个规则可以用文字描述如下:( L ) (L) ( L ) x ( 0 ) \boldsymbol x^{(0)} x ( 0 ) j j j x j ( 0 ) x_j^{(0)} x j ( 0 ) ( D ) (D) ( D ) j j j w ( 0 ) \boldsymbol w^{(0)} w ( 0 ) j j j x j ( 0 ) = 0 x_j^{(0)}=0 x j ( 0 ) = 0 ( D ) (D) ( D ) w ( 0 ) \boldsymbol w^{(0)} w ( 0 ) i i i w i ( 0 ) w_i^{(0)} w i ( 0 ) ( L ) (L) ( L ) i i i
通过互补松弛性质,我们可以快速地根据对偶问题的最优解直接求出其原问题的最优解 ——根据对偶问题的最优解与0的大小关系,列出原问题最优解应该满足的等式线性方程组,并求解之。
比如下面这个例题:
对偶单纯形法 考虑我们之前一直研究的标准型 LP(记作L L L
min c x s. t. A x = b x ≥ 0 \begin{aligned} \min\quad&\boldsymbol{cx}\\ \text{s. t. }\quad&\boldsymbol{Ax=b}\\ &\boldsymbol{x\geq0} \end{aligned} min s. t. cx Ax = b x ≥ 0
之前我们为了得到一个基本可行解以便使用单纯形法,往往引入人工变量 并通过两阶段法来处理。而利用对偶性质 ,我们可以给出一种不用人工变量的方法。为此,我们先引入对偶可行的基本解 的概念:
设x ( 0 ) \boldsymbol x^{(0)} x ( 0 ) ( L ) (L) ( L ) 基本解 (可以“不可行”,即不一定满足约束条件),它对应的基矩阵为B \boldsymbol B B 单纯形乘子 w = c B B − 1 \boldsymbol {w=c_B B}^{-1} w = c B B − 1 w \boldsymbol w w ( L ) (L) ( L ) ( D ) (D) ( D ) 可行解 ,即满足对偶问题( D ) (D) ( D ) ∀ j , w p j − c j ≤ 0 \forall j,\;\boldsymbol {wp}_j-c_j\leq0 ∀ j , wp j − c j ≤ 0 所有判别数 都小于等于零,那么就称x ( 0 ) \boldsymbol x^{(0)} x ( 0 ) ( L ) (L) ( L ) 对偶可行的基本解 。
基本思想与计算步骤 原版单纯形法是保持原问题基本解可行 的情况下(其实就是保持右端列b ˉ \bar{\boldsymbol b} b ˉ
而对偶单纯形法的思路则是不断改进对偶问题的基本可行解 ,当对偶基本可行解改进后也能使得原问题的基本解变得可行 时(其实就是右端列b ˉ \bar{\boldsymbol b} b ˉ
为了尽可能让右端列b ˉ \bar{\boldsymbol b} b ˉ 先选择离基变量再选择出基变量 。b ˉ \boldsymbol {\bar b} b ˉ 负数中最小 的那一行,因为这样可以在主元消去时尽可能让更多的b i b_i b i
b ˉ r = min i { b ˉ i } < 0 \bar{b}_r=\min_i\{\bar{b}_i\}\lt0 b ˉ r = i min { b ˉ i } < 0
然后是进基变量的选择。为了保证主元消去后判别数仍然小于或等于零(即保证w \boldsymbol w w
z k − c k y r k = min j { z j − c j y r j ∣ y r j < 0 } \frac{z_k-c_k}{y_{rk}}=\min_{j}\left\{\frac{z_j-c_j}{y_{rj}}\bigg|y_{rj}\lt0\right\} y r k z k − c k = j min { y r j z j − c j y r j < 0 }
当主行无负元,即∀ j , y r j ≥ 0 \forall j,\;y_{rj}\geq0 ∀ j , y r j ≥ 0 x \boldsymbol x x 非负 的值都不能满足第r r r 原问题无可行解 。 对偶问题的最优解 就是原问题最终单纯形表中松弛变量的判别数的相反数 。(可根据对偶性质的推论得来)初始对偶可行的基本解 对偶单纯形法同样面临一个问题,那就是要先找到一个对偶可行的基本解,也就是说要找到一个可以使得判别数非正的基本解。为此,类比两阶段法,我们需要先解一个扩充问题 。
我们将原问题的约束条件( B , N ) ⋅ ( x B x N ) = b \boldsymbol{(B,N)·\begin{pmatrix}\boldsymbol x_B\\\boldsymbol x_N\end{pmatrix}=b} ( B , N ) ⋅ ( x B x N ) = b B − 1 B^{-1} B − 1
B − 1 B x B + B − 1 N x N = B − 1 b i . e . x B + ∑ j ∈ R y j x j = b ˉ \begin{aligned} B^{-1}B\boldsymbol x_B+B^{-1}N\boldsymbol x_N&=B^{-1}\boldsymbol b\\\\ i.e.\quad\; \boldsymbol x_B+\sum_{j\in R}\boldsymbol y_jx_j&=\bar{\boldsymbol b} \end{aligned} B − 1 B x B + B − 1 N x N i . e . x B + j ∈ R ∑ y j x j = B − 1 b = b ˉ
其中,R R R y j = B − 1 p j \boldsymbol y_j=B^{-1}\boldsymbol p_j y j = B − 1 p j x \boldsymbol x x x B , x N \boldsymbol x_B,\boldsymbol x_N x B , x N
此外,我们再增加一个变量x n + 1 x_{n+1} x n + 1
∑ j ∈ R x j + x n + 1 = M \sum_{j\in R}x_j+x_{n+1}=M j ∈ R ∑ x j + x n + 1 = M
其中,M M M 扩充问题 :
min c x s. t. x B + ∑ j ∈ R y j x j = b ˉ ∑ j ∈ R x j + x n + 1 = M x ≥ 0 , x n + 1 ≥ 0 \begin{aligned} \min\quad&\boldsymbol{cx}\\ \text{s. t. }\quad&\boldsymbol x_B+\sum_{j\in R}\boldsymbol y_jx_j=\bar{\boldsymbol b}\\ &\sum_{j\in R}x_j+x_{n+1}=M\\ &\boldsymbol{x\geq0},\;x_{n+1}\geq0 \end{aligned} min s. t. cx x B + j ∈ R ∑ y j x j = b ˉ j ∈ R ∑ x j + x n + 1 = M x ≥ 0 , x n + 1 ≥ 0
通过扩充问题,我们得到如下求解策略:
利用"原始" Simplex 进行主元消去,直到− ∇ f ( x ) ≤ 0 -\nabla f\boldsymbol{(x)\leq0} − ∇ f ( x ) ≤ 0 利用对偶 Simplex 进行主元消去,直到b ˉ ≥ 0 \bar{\boldsymbol b}\geq0 b ˉ ≥ 0 注:上述策略中,“原始” Simplex 是打双引号的。无条件选择 m + 1 m+1 m + 1 − ∇ f ( x ) ≤ 0 -\nabla f\boldsymbol{(x)\leq0} − ∇ f ( x ) ≤ 0
此外还有,可以证明:
扩充问题没有可行解时,原问题也没有可行解 ;扩充问题的最优值与M M M x n + 1 x_{n+1} x n + 1 n n n ;扩充问题的最优值与M M M x n + 1 x_{n+1} x n + 1 。原始-对偶算法 待更
C++实现 建立单纯形法类 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #ifndef SIMPLEX_H #define SIMPLEX_H #include <cstdlib> struct solution { double f; double *discri; double *x; int tag=0 ; }; template <std::size_t M, std::size_t N>class Simplex { private : int m = M, n = N; double (*A)[N]; double *b; double b_bar[M]; double *c; int base_list[M]; solution res; public : Simplex <M,N>(double A[M][N], double b[M], double c[N]): A (A),b (b),c (c){} ~Simplex (){} void UpdateBaseVars_Im () void UpdateDIscri () void Solve_Im () void TwoStepMethod () solution GetSolution () ; }; #endif
第一次迭代 接下来是针对第一次迭代 进行初始化 。
第一步是先找出可以组成单位矩阵I m I_m I m base_list[M] 存储,内容是基变量对应的下标。通过类方法 Simplex::UpdateBaseVars_Im() 实现。
第二步是根据公式计算判别数。这里用 discri[N] 存储,基变量对应的判别数置0,对应着单纯形表的最后一行。通过类方法 Simplex::UpdateDIscri() 实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include "Simplex.h" #include "string.h" #include <iostream> using namespace std;template <std::size_t M, std::size_t N>void Simplex<M,N>::UpdateBaseVars_Im (){ memset (base_list, 0 , sizeof (int )*m); int cnt, idx, k=0 ; for (int j = 0 ; j < n; j++){ cnt = 0 ; idx = -1 ; for (int i = 0 ; i < m; i++){ if (A[i][j] != 0 && A[i][j] != 1 ) break ; if (A[i][j] == 0 ) cnt++; if (A[i][j] == 1 ) idx=i; } if (cnt == m-1 && idx != -1 && A[idx][j] == 1 ){ base_list[idx] = j; } } } template <std::size_t M, std::size_t N>void Simplex<M,N>::UpdateDIscri (){ res.discri = new double [n]; memset (res.discri, 0 , sizeof (double )*n); for (int j = 0 ; j < n; j++){ for (int i = 0 ; i < m; i++){ if (base_list[i] == j){ res.discri[j] = 0 ; break ; }else { res.discri[j]+=A[i][j]*c[base_list[i]]; } } res.discri[j] -= c[j]; } }
多次迭代求解 接下来是从第二次迭代开始直到算法结束的整个迭代过程。
首先计算现行目标函数值 f,然后根据 discri[N] 找到主列 main_col,如果判别数全小于0则说明达到最优解 ,否则如果 A[main_col] 所有元素都小于0则说明原问题无界 。
如果没有以上两种问题,则根据 b_bar[M]/A[main_col] 寻找主行 main_row,最后利用主元消去法 进行矩阵 A 的更新、判别数 discri[N] 和基变量 base_list[M] 的更新。
为了应对可能出现循环的那一类 LP 问题,通过设置最大迭代次数 iter_nums 规避无限循环。
最终的最优解由 b_bar[M] 对应的基变量取特定的值得到,而非基变量的取值为0。通过类方法 Simplex::GetSolution() 得到结果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 template <std::size_t M, std::size_t N>void Simplex<M,N>::Solve_Im (){ UpdateBaseVars_Im (); res.f = 0 ; for (int i = 0 ; i < m; i++){ b_bar[i] = b[i]; res.f += c[base_list[i]]*b_bar[i]; } UpdateDIscri (); int cnt,T=1 ; int iter_nums=100 ; int main_col; int main_row; double A_tmp[M][N]; while (iter_nums--){ main_col = 0 ; main_row = 0 ; for (int j = 0 ; j < n; j++){ if (res.discri[main_col] < res.discri[j]){ main_col = j; } } if (res.discri[main_col] <= 0 ) return ; cnt = 0 ; for (int i = 0 ; i < m; i++){ if (A[i][main_col] < 0 ) cnt++; if (A[main_row][main_col] < 0 ) main_row = i; if (b_bar[main_row]/A[main_row][main_col] > b_bar[i]/A[i][main_col] && A[i][main_col] >= 0 ){ main_row = i; } } if (cnt == m){res.tag = -1 ; return ;} res.f -= b_bar[main_row]/A[main_row][main_col]*res.discri[main_col]; for (int i = 0 ; i < m; i++){ if (i == main_row) b[i] = b_bar[i]/A[main_row][main_col]; else b[i] -= b_bar[main_row]/A[main_row][main_col]*A[i][main_col]; } for (int j = 0 ; j < n; j++){ if (j == main_col) continue ; res.discri[j] -= A[main_row][j]/A[main_row][main_col]*res.discri[main_col]; } res.discri[main_col] = 0 ; T++; cout << "@第" << T << "次迭代:" << endl; cout << "--------------------------------------------------------" << endl; for (int i = 0 ; i < m; i++){ for (int j = 0 ; j < n; j++){ if (i == main_row) A_tmp[i][j] = A[i][j]/A[main_row][main_col]; else A_tmp[i][j] = A[i][j]-A[main_row][j]/A[main_row][main_col]*A[i][main_col]; cout << A_tmp[i][j] << "\t" ; } b_bar[i] = b[i]; cout << "|" << b[i] << endl; } cout << "--------------------------------------------------------" << endl; for (int i = 0 ; i < m; i++){ for (int j = 0 ; j < n; j++){ A[i][j] =A_tmp[i][j]; } } for (int j = 0 ; j < n; j++){ cout << res.discri[j] << "\t" ; } cout << "f=" << res.f << endl; cout << "---------------------------------------------------------" << endl << endl; base_list[main_row] = main_col; } } template <std::size_t M, std::size_t N>solution Simplex<M,N>::GetSolution (){ res.x = new double [n]; memset (res.x, 0 , sizeof (double )*n); for (int i = 0 ; i < m; i++){ res.x[base_list[i]] = b_bar[i]; } return res; }
求解测试 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 #include <iostream> #include <cstdlib> #include "Simplex.h" using namespace std;int main (void ) double A[3 ][5 ] = {{1 ,-2 ,1 ,0 ,0 }, {0 ,1 ,-3 ,1 ,0 }, {0 ,1 ,-1 ,0 ,1 }}; double b[3 ] = {2 ,1 ,2 }; double c[5 ] = {0 ,-1 ,2 ,0 ,0 }; Simplex<3,5> myQuestion (A,b,c) ; myQuestion.Solve_Im (); solution res = myQuestion.GetSolution (); cout << "最优解: [ " ; for (int i = 0 ; i < 5 ; i++) cout << res.x[i] << ", " ; cout << "];" << endl; cout << "最优值: f_min = " << res.f << endl; return 0 ; }
Python scipy.optimize模块也能实现 ,但不及下述两种库,此处略过
PuLP库1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 from pulp import *import pandas as pdimport numpy as npimport mathWB = pd.read_csv('BCHAIN-MKPRU.csv' ) WG = pd.read_csv('LBMA-GOLD.csv' ) WBWG = pd.merge(WB, WG, how='outer' , on='Date' ) WBWG.to_csv('MergeData.csv' ,index=False ) NanIdx = WBWG[WBWG['USD (PM)' ].isnull()].index prob = LpProblem("The_Ideal_situation" ,LpMaximize) xGs = [f'xG{i} ' for i in range (0 ,1826 )] xBs = [f'xB{i} ' for i in range (0 ,1826 )] iGs = [f'iG{i} ' for i in range (0 ,1826 )] iBs = [f'iB{i} ' for i in range (0 ,1826 )] xG = LpVariable.dicts("xG" ,xGs,0 ,None ,LpContinuous) xB = LpVariable.dicts("xB" ,xBs,0 ,None ,LpContinuous) iG = LpVariable.dicts("iG" ,iGs,-1 ,1 ,LpInteger) iB = LpVariable.dicts("iB" ,iBs,-1 ,1 ,LpInteger) C = 1000 G = 0 B = 0 for i in range (10 ): C += -(iB[f'iB{i} ' ]+0.0002 )*xB[f'xB{i} ' ]*WBWG.loc[i,'Value' ] G += xG[f'xG{i} ' ] B += xB[f'xB{i} ' ] if not math.isnan(WBWG.loc[i,'USD (PM)' ]): C += -(iG[f'iG{i} ' ]+0.0001 )*xG[f'xG{i} ' ]*WBWG.loc[i,'USD (PM)' ] prob += C+WBWG.loc[10 ,'Value' ]*B+WBWG.loc[10 ,'USD (PM)' ]*G C = 1000 G = 0 B = 0 for i in range (10 ): C += -(iB[f'iB{i} ' ]+0.0002 )*xB[f'xB{i} ' ]*WBWG.loc[i,'Value' ] G += xG[f'xG{i} ' ] B += xB[f'xB{i} ' ] if not math.isnan(WBWG.loc[i,'USD (PM)' ]): C += -(iG[f'iG{i} ' ]+0.0001 )*xG[f'xG{i} ' ]*WBWG.loc[i,'USD (PM)' ] prob += C >= 0 prob += G >= 0 prob += B >= 0 for i in NanIdx: if i > 9 : break prob += var[f'xG{i} ' ] == 0 prob.to_json("Ideal_solution.json" ) prob.solve() print ("\n" ,"status: " ,LpStatus [prob.status] ,"\n" )Name = [] Value = [] for v in prob.variables() : Name.append(v.name) Value.append(v.varValue) pd.DataFrame({"VarName" :Name,"VarValue" :Value}).to_csv("IdealResult.csv" ,index=False ) print ("Maximun Advantage =" , "Rs" , value(prob.objective))
cvxpy库max x G k , x B k , 1 ≤ k ≤ K C K + G K W G K + B K W B K s . t . { C 0 = 1000 , G 0 = 0 , B 0 = 0 C k + 1 = C k − x G k W G k − x B k W B k − α b i t c o i n % ∣ x G k ∣ W G k − α g o l d % ∣ x B k ∣ W B k G k + 1 = G k + x G k B k + 1 = B k + x B k C k , G k , B k ≥ 0 k = 1 , 2 , . . . , K \max_{x_G^k,x_B^k,1\leq k\leq K} C^K+G^KW_G^K+B^KW_B^K\\ s.t.\begin{cases} C^0=1000,G^0=0,B^0=0\\ C^{k+1}=C^k-x_G^kW_G^k-x_B^kW_B^k-\alpha_\mathbf{bitcoin}\%|x_G^k|W_G^k-\alpha_\mathbf{gold}\%|x_B^k|W_B^k\\ G^{k+1}=G^k+x_G^k\\ B^{k+1}=B^k+x_B^k\\ C^k,G^k,B^k \geq 0 \\ k=1,2,...,K \end{cases} x G k , x B k , 1 ≤ k ≤ K max C K + G K W G K + B K W B K s . t . ⎩ ⎨ ⎧ C 0 = 1000 , G 0 = 0 , B 0 = 0 C k + 1 = C k − x G k W G k − x B k W B k − α bitcoin %∣ x G k ∣ W G k − α gold %∣ x B k ∣ W B k G k + 1 = G k + x G k B k + 1 = B k + x B k C k , G k , B k ≥ 0 k = 1 , 2 , ... , K
以上述模型为例,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 import mathimport pandas as pdimport numpy as npimport cvxpy as cpWB = pd.read_csv('BCHAIN-MKPRU.csv' ) WG = pd.read_csv('LBMA-GOLD.csv' ) WBWG = pd.merge(WB, WG, how='outer' , on='Date' ) WBWG.to_csv('MergeData.csv' ,index=False ) NanIdx = WBWG[WBWG['USD (PM)' ].isnull()].index C = 1000 ;G = 0 ;B = 0 cons = [] xG = cp.Variable(1826 ) xB = cp.Variable(1826 ) for i in range (1826 ): C -= 0.0002 *WBWG.loc[i,'Value' ]*cp.abs (xB[i])+xB[i]*WBWG.loc[i,'Value' ] G += xG[i] B += xB[i] if not math.isnan(WBWG.loc[i,'USD (PM)' ]): C -= 0.0001 *WBWG.loc[i,'USD (PM)' ]*cp.abs (xG[i])+xG[i]*WBWG.loc[i,'USD (PM)' ] cons.append(C >= 0 ) cons.append(G >= 0 ) cons.append(B >= 0 ) func = cp.Maximize(C+G*WBWG.loc[1825 ,'USD (PM)' ]+B*WBWG.loc[1825 ,'Value' ]) for i in NanIdx: cons.append(xG[i] == 0 ) prob = cp.Problem(func,cons) prob.solve() print ("\nstatus:" , prob.status)print ("\nThe Maximun Advantage is: " , prob.value)pd.DataFrame({"Gold" :np.around(xG.value, 2 ),"Bitcoin" :np.around(xB.value, 2 )}).to_csv("IdealResult.csv" ,index=False )
参考 陈宝林 编著. 《最优化理论与算法》. 清华大学出版社. ISBN : 978-7-320-11376-8 凸优化高质量开源课程 - 美国卡内基梅隆大学