解构城市可达性与设施分布的规律
📑 原始论文:Deconstructing laws of accessibility and facility distribution in cities
摘要
汽车时代严重降低了城市生活质量,造成昂贵的出行和明显的环境影响。新的城市规划范式必须成为我们未来路线图的核心,使得居民可以在几分钟内通过自行车或步行获得基本生活需求。在这项工作中,我们提出了设施和人口分布之间相互作用的新颖见解,以最大程度地提高现有道路网络的可达性。在六个城市的结果显示,通过重新分配设施,旅行成本可以减少一半。在最佳方案中,平均旅行距离可以被建模为设施数量和人口密度的函数的形式。作为这一发现的应用,可以根据城市的人口分布估计达到所需平均旅行距离所需的设施数量。
拆解一下,本文章的核心贡献总结如下:
- 使用优化算法得到最优设施分配;
- 探索了最优分配和当前分配的差距,并且说明不符合传统2/3幂律分布;
- 建模了平均出行距离与人口密度、设施数量的关系。做了一堆近似化简之后,得出只与设施数量有关的函数表达式。
优化方案
- 前提假设:作者以 1km × 1km 的网格作为一个 block,并且假设一个 block 里面每一类设施(facility)只能设立一个;
- 距离选取:不以泰森多边形中心点之间的欧氏距离,而是构建出网络流图,使用 Dijkstra 算法计算两两节点间的距离。综合各个 block 内的人口数量计算出从-th block 到-th block 的总出行代价,记为;
- 决策变量:用 表示离-th block 最近的带有设施的block是-th block;用 表示-th block内有设施;所以,当且仅当 时, 才有机会等于1,否则-th block内都没有设施了,就不存在“离-th block 最近的带有设施的block是-th block” 这个说法了。综上可以把这两种情况统一写成.
设施选址问题是经典的运筹优化问题。而本文目标是最小化到设施的总距离,这是一个经典的 NP hard 问题,并且常被成称为-median Problem(p-中位数问题)。
本文作者直接沿用了论文《A fast swap-based local search procedure for location problems.》的方法来求解该问题.
NOTE:本文章对设施的分配是依次按照不同类别来分配的。也就是说,比如先对
hospital这个类别的设施进行优化,得出哪些block该设置医院,那些block不设置医院。然后再优化下一类的设施。此外,本文章的优化决策不考虑增设设施数量的情形,即重分配前有多少个医院,分配后也只有多少个医院,只是其地理位置可能不变。这也是自然的,不做这个假设的话,问题背景就不符合经典运筹学问题 设施选址问题 的定义了,作者为了利用经典算法解决问题,只能这么假设了。
统计探索
作者将每一种设施单独抽离出来,所有内含该设施的 block 组成的集合被命名为服务社区(Service community)。考察其中一种设施(比如 hospital)的服务社区里的出行距离、人口数量等关系。其实这是显然的,因为他在求优化问题时本来就分不同类设施来分别优化了,所以得出的结果也是分好的,这里他为了后面方便说明才在论文里提出了所谓服务社区的概念,其实没什么用。
另外,为了说明“我们的分配比以前的好”,并且为了后续便于区分,作者先定义分配之前的方案叫做实际场景(actual senarios),而自己的分配方案叫做最优场景(optimal senarios)。
增益指数
设增益指数(gain index)为,是-th block 到离它最近的设施的距离,最优比上实际场景。所以 就说明新的分配越好。
除了在微观的-th block 上进行探索,还可以结合人口数量,计算总的出行距离,以便查看 city-level 的情况,作者称之为optimality index R:
画图时还可以取对数将数值划分出正负,清晰直观。同时还可以计算对应的基尼系数作图,基尼系数的值在0到1之间。
幂律关系
传统研究在更为全局的尺度上给出了设施密度 和 人口密度 之间满足:
这里作者在 block-level 下利用最小二乘法做拟合,指出“在微观层面就不满足这种关系了”。
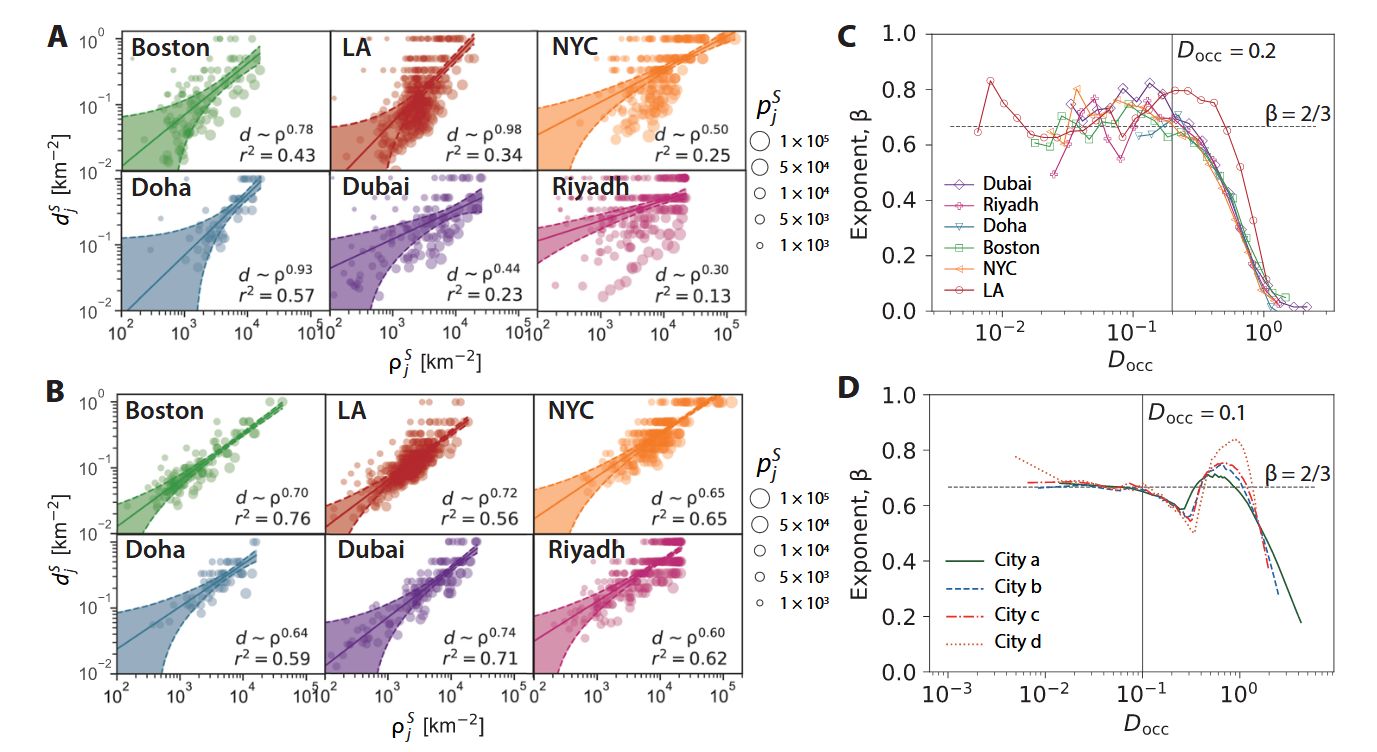
函数建模
为了建模出平均出行距离 和其他变量之间的关系,作者给出了下面这个公式:
为城市总人口
是事先假设的最小块内距离, 是第 个block的面积,因为是取的 1km × 1km 方格,所以这里略过
表示第 个设施的服务社区(Service community)中的人口数量
表示不在第 个设施的服务社区中的人口数量
代表第 个设施的服务社区中超过人口阈值的那些block的面积,对它求根号可以得到一个近似的单位距离
代表第 个设施的服务社区中的几何因子,作为一个社区中的平均出行距离的比例系数,这里限定每个城市固定共用同一个因子。所以 就是一个社区可用的平均距离的估计值
一言蔽之,设施 的平均出行距离 由两部分组成,分别是内含有设施的那些 block 的总距离和需要跨越 block 的总距离。即,在社区内的和不在社区内的。
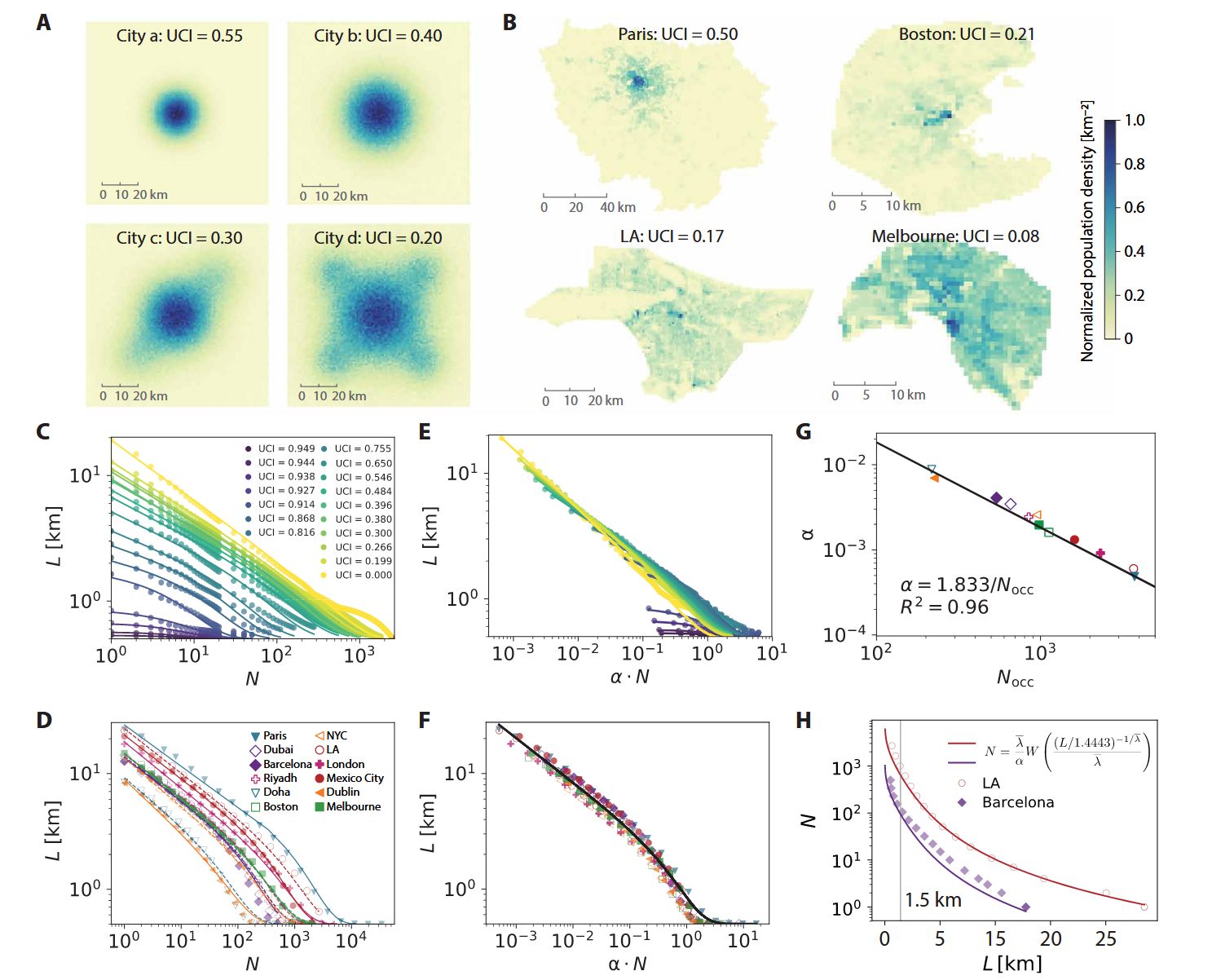
作者进行了一通近似和利用相关性缩减自变量,最后得到:
然后探索了不同城市中心性(Urban centrality index)拟合上面这个公式时得到的参数。




