问题是什么？

这次问题的提出，同样是根据我最近训练的数学建模题而散发出来的。

原问题所依托的背景是：

某交警中队根据其辖区交通实际状况，通常把该辖区划分为若干责任区。
每个责任区都委派一名交警进行交通事故处理，即每名交警仅负责其责任区内的所有交通事故的警情处理。
为均衡每名交警的工作量，交警中队管理部门需要把该辖区划分为若干警情总量尽可能均衡的责任区。

划分辖区的方式大致如下：

划分示例

值得注意的是，每一个辖区的交通事故易发点之间应该是可达的，而每个区域的警情量总和在总体上是大致均等的。

数学抽象

根据问题描述，可以简单将其抽象为一个 顶点赋权无向图 的划分问题。

具体来说，就是对一个顶点权值集合为 $W$ 的无向图 $G<V,E>$ 进行划分，得到对应的 $k$ 个子图 $G_1<V_1,E_1>、G_2、...、G_k$ .

其中有 $V_1\cup V_2\cup ...\cup V_k=V$ ，且 $V_i \cap V_j=\emptyset$ ，其中， $i\neq j\;\;and\;\; i,j=1,2,...,k$

定义 $G_i$ 的连通分支数为 $p(G_i)$ ，则有： $\forall G_i,p(G_i)=1$

于是得到规划模型：

$\min{\sum_{i=1}^k|\sum_{j=1}^{|V_j|}w_{ij}-\frac{1}{n}\sum_{j=1}^nw_{j}|} \\s.t.\begin{cases} V_1\cup V_2\cup ...\cup V_k=V\\ V_i \cap V_j=\emptyset\\ p(G_i)=1\\ i\neq j\;\;and\;\; i,j=1,2,...,k \end{cases}$

图划分问题Ⅰ

根据以上解析，可以发现这题的难点集中在图划分上。所以如何合理的进行图划分就是一个值得思考的问题了。

随机划分

本问题我一开始的想法就是利用随机优化算法，例如模拟退火算法来处理，于是我最先想到的方法自然就是随机划分。

例如，邻接矩阵随机取点法。

对于任意一个图 $G<V,E>$ 的邻接矩阵：

$A=\left[ \begin{matrix} &c&c&b&b&c&\\ &c&c&b&b&c&\\ &b&b&a&a&b&\\ &b&b&a&a&b&\\ &c&c&b&b&a\\ \end{matrix} \right]$

为将其分为两个子图 $G_1、G_2$ ，可在 $A$ 中任意抽取任意数量的行列（行列必须一一对应）并将其重组得到两个新的邻接矩阵。

例如上式中，将第3、4行以及对应的3、4列整体移出，可得到：

$A_1=\left[ \begin{matrix} &a&a&\\ &a&a&\\ \end{matrix} \right], A_2=\left[ \begin{matrix} &c&c&c&\\ &c&c&c&\\ &c&c&c&\\ \end{matrix} \right]$

于是，可以通过分别对这两个新的邻接矩阵计算可达矩阵或连通分支数，只要判断连通即可。

注：无向图的邻接矩阵应该是对称矩阵，此处的a,b,c并非具体数值，而是位置标记。

又或者，随机去边法。

1）简化读取量。不通过邻接矩阵，直接读取无向图的连通情况表，即一个 $1\times2$ 的矩阵，第一列和第二列对应的点相互连通。

2）随机割边。对连通矩阵随机删除一个点对点的连通对。

3）计算割边后得到的新图的连通分支数，如果是k则退出，并导出此时的k个点集，否则回到第一步。

然而，这样的算法随机性太大，事实上当数据量很大时，二者很难收敛到最优解，况且每一边随机生成都要判断一次连通性。总体来说，如果没有好的生成解的方式和更新解的方式，那所谓 模拟退火、遗传算法就和 蒙特卡洛完全没有区别了，只是迭代次数的问题。

综上所述，我需要找到一个尽可能好的划分策略，以及更新解的方式。

顶点蔓延划分

接下来，将阐述我的“自创划分”的算法，来实现原始解的生成。

首先，由于问题要求的是划分的子图顶点和较为均衡，因此可以考虑在生成解的时候，就尽量利用贪心的思考方式，产生一个较为合理的近似解。

于是，考虑如下算法进行解的生成：

找到所给图的顶点中，权值最大的 $k$ 个顶点
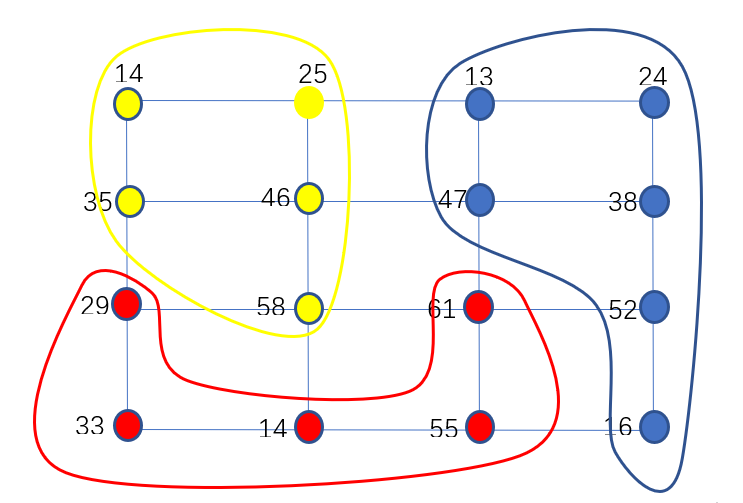
此处以二分为例给出算法图示，图中红色点为最大的两个点
以这 $k$ 个点为基准，以是否连通为条件，分别自主地向周围的点蔓延，直到所有的点都被覆盖

事实上，想要实现这样的算法，也不难，下面以matlab为例给出一种实现方法，利用了多组并行BFS（宽度优先搜索）的思想。

function [Vn] = graphcut(W,chaos,k,num)
%GRAPHCUT 顶点蔓延算法实现图的均匀k划分
%   W为顶点权值，chaos为点对点cell数组
%   num为顶点个数
%   返回k个向量，用cell数组整合
V = zeros(1,num);
quzu = cell(1,k);%分配k个队列
tmp = 0;
[Wn,max_idx] = sort(W,'descend');% 降序得到前k个最大权值顶点
while find(V==0)
    %前k个最大顶点分别压入k个队列中
    for i =1:k
        V(max_idx(i)) = i;
        cur = chaos{max_idx(i)};
        quzu{i}{1} = cur;%入栈
    end
    while tmp ~= k
        tmp = 0;
        for i = 1:k
            if ~isempty(quzu{i})
                cur = quzu{i}{1};
                len = length(cur);
                for j = 1:len
                    if V(cur(j)) == 0
                        V(cur(j)) = i;
                        quzu{i}{end+1} = chaos{cur(j)};
                    end
                end
                quzu{i}(1) = [];%出栈
            else
                % 如果某顶点蔓延完毕，计数+1
                % 当且仅当所有顶点全蔓延完毕时，tmp==k，循环打破
                % 否则tmp会在下一次循环中清零
                tmp = tmp + 1;
            end
        end 
    end
end
% 获取分组结果，此时所有点都被遍历，即是V不会有0，所以跳出了循环
Vn = cell(1,k);
for i = 1:k
    Vn{i} = find(V==i);
end
end

注：上述函数中的chaos参数，为一种 并查集 思想的数据结构。

大致思路为：以索引/下标作为顶点编号，该索引下的内容为与这个顶点直接相连的点的集合。

举例如下：

并查集举例

于是有：

$a[1]=\{2,3,4\}$

$a[2]=\{1,5\}$

$a[3]=\{1\}$

……

解的更新

判断连通性

得益于上述数据结构的“便利性”，我们可以对一组解是否连通进行BFS判断，算法如下：

将子集 $V$ 的第一个顶点 $i$ 作为起始点进行遍历
对 $i$ 的 $chaos[i]$ 下的点进行标记，并以标记作为基准判断是否压入队列
以队列顶部的顶点作为 $i$ ，执行第二步直到队列内没有顶点
判断子集中的顶点是否都被标记，如果是则说明 $V$ 中的子集构成的图 $G$ 为连通的，否则不连通

点交换

根据上述原始解的生成，我们可以巧妙的设置新解的产生，即对原解中的划分边缘点进行交换。

点交换

问题有三，一是如何判断什么是 边缘点；二是如何判断是否可以交换；三是交换后能否保证新子图是连通图。

关于问题一。可以利用前面提到的 $chaos[i]$ 进行处理，思路是，先随机取点，判断与该点直接相连的点是否都是属于自己所在的子图。

以上图中的左图为例，有 $V_{左}={1，2，3，4，5}$ ，而点(5)有 $chaos[5]=\{2,4,6\}$ ，其中， $6\notin V_{左}$ ，所以，5是边缘点。

那会不会存在 所有的点内直达点都在集合内 的情况呢？答案是，有的。这种情况只会出现在另一个集合为空集的时候。然而由于我们前面产生的原始解不会有这种情况出现，所以无需担心。

关于问题二。如果自身所在的子集只有一个元素，就肯定不能将自己交换出去。因为当自己被其他子集划过去后，当前子集就变为了空集，既不符合题意，也会让上一个问题得不到解决。

关于问题三。第一，因为我们是通过找寻边缘点进行交换的，所以当把当前锁定的边缘点划分过去目标子集时，目标子集会在原本自身就连通的情况下，再加一个连通的顶点，即是目标子集绝对不会不连通。因此，仅需对边缘点当前所在的子集进行假设判断。判断如果边缘点离开当前集合后得到的新集合是否仍然连通，这是必要的。

特殊情况

如上图所示，如今将图中的顶点(1)进行割舍，就会导致点2、3、4全部变为孤立点。

代码

于是，可以得到完美解决该问题的代码：

function [Vn] = rewrite(chaos,V,k,num)
%REWRITE 对k个子图划分进行寻优调整
while 1
    Vn = V;
    % 随机选取一个点集n
    n = unidrnd(k);
    len = length(Vn{n});
    % 如果这个子图只包含一个顶点，则换一个子图进行处理
    if len == 1
        break;
    end
    % 选取n的任意一个顶点tmp
    m = unidrnd(length(Vn{n}));
    tmp = Vn{n}(m);
    % 找寻与tmp相连通但不属于n的点point
    flag = 0;
    for point = chaos{tmp}
        if ~ismember(point,Vn{n})
            flag = 1;
            break;
        end
    end
    % 如果没找到，继续
    if ~flag
        continue;
    end
    % 判断tmp划到与它连通的i所在的子集后，原子集是否连通
    Vn{n}(m) = [];
    qu = Vn{n}(1);
    visit = zeros(1,num);
    visit(qu(1)) = 1;
    while ~isempty(qu)
        cur = qu(1);
        for i = chaos{cur}
            if visit(i) ~= 1 && ismember(i,Vn{n})
                visit(i) = 1;
                if ~ismember(i,qu)
                    qu(end+1) = i;
                end
            end
        end
        qu(1) = [];
    end
    % 如果不连通，重新划分
    if find(visit(Vn{n})==0)
        Vn = V;
        break;
    end
    % 否则，将tmp划到其他子集中
    for j = 1:k
        if ismember(point,Vn{j})
            Vn{j}(end+1) = tmp;
            flag = 0;
            break;
        end
    end
    if ~flag
        break;
    end
end
end