哈夫变换 基本哈夫变换 点线对偶性 y = p x + q y=px+q y = p x + q
X Y XY X Y P Q PQ PQ
q = − p x + y q=-px+y q = − p x + y
检测步骤 根据点线对偶性,可以基于投票算法的思想,设计出如下算法以实现检测一系列X Y XY X Y ( x i , y i ) (x_i,y_i) ( x i , y i ) y = p x + q y=px+q y = p x + q
其中,参数( p , q ) (p,q) ( p , q )
我们可以在参数空间P Q PQ PQ p , q p,q p , q
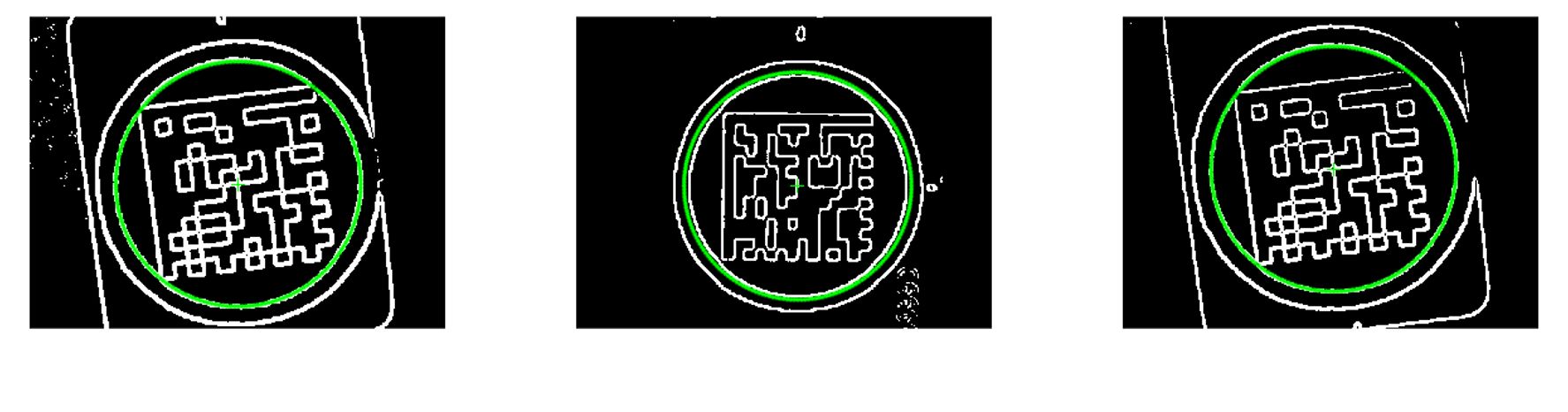
对参数空间中的参数p , q p,q p , q A [ p min . . p max , q min . . q max ] A[p_{\min}..p_{\max},\;q_{\min}..q_{\max}] A [ p m i n .. p m a x , q m i n .. q m a x ] 对X Y XY X Y ( x i , y i ) (x_i,y_i) ( x i , y i ) p p p q = − p x i + y i q=-px_i+y_i q = − p x i + y i q q q p , q p,q p , q A [ p , q ] ← A [ p , q ] + 1 A[p,q]\leftarrow A[p,q]+1 A [ p , q ] ← A [ p , q ] + 1 找出A A A ( p , q ) (p,q) ( p , q ) DM码的定位与读取 目标识别 边缘检测 为了能够识别DM码中的定位,我们首先需要对其进行边缘检测,从而将检测结果用于识别。
测试发现,如果先将图片进行滤波降噪再检测,效果会好很多。5 × 5 5\times 5 5 × 5 盒式滤波器 进行模糊。S o b e l Sobel S o b e l 算子 进行边缘检测。
而H o u g h Hough Ho ug h
Image dm1dm2dm3Threshold 0.1 0.5 0.4
圆检测 MATLAB 中并没有提供利用H o u g h Hough Ho ug h Weisong Zhao 编写的代码.
他提供的 Hough_circle 函数需要给定二值图、半径步长、最小半径、最大半径、选取阈值 的参数。
Image dm1dm2dm3( R m i n , R m a x ) (R_{min},R_{max}) ( R min , R ma x ) (150, 170) (110, 130) (150, 170)
此处给出的代码仅给出了对 dm1.bmp 的处理,其他图片的处理是类似的,因此省略。下同
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 close all;clear;clc; dm1 = im2double(imread('DM01.bmp' )); box_H = 1 /25 *ones (5 ,5 ); dm1 = imfilter(dm1,box_H); dm1_sobel = abs (imfilter(dm1,fspecial('sobel' )'))+... abs (imfilter(dm1,fspecial('sobel' ))); dm1_sobel(dm1_sobel>0.1 ) = 1 ; dm1_sobel(dm1_sobel<0.1 ) = 0 ; [Hough_space,Hough_circle_result,Para] = Hough_circle(dm1_sobel,5 ,0.1 ,150 ,170 ,0.6 ); figure ; imshow(dm1_sobel);hold on;t=0 :0.01 *pi :2 *pi ; plot (Para(:,2 ), Para(:,1 ), 'g+' );plot (cos (t).*Para(1 ,3 )+Para(1 ,2 ),sin (t).*Para(1 ,3 )+Para(1 ,1 ),'g.' );
直线检测 防止DM码外部的直线对检测进行干扰,我们先根据检测得到的圆的位置信息进行图像过滤,即将圆外的二值图全部置0.
之后,我们再利用 自带的 hough、houghpeaks、houghlines 函数进行直线检测。
由于已经提取到了圆内的图像,并且DM码的“最大可投票”的直线就是我们需要的那两条,这里我们选取2作为极值个数正好满足需求。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 for i = 1 :size (dm1_sobel,1 ) for j = 1 :size (dm1_sobel,2 ) if ((i -Para(1 ,1 ))^2 +(j -Para(1 ,2 ))^2 > Para(1 ,3 )^2 ) dm1_sobel(i ,j ) = 0 ;dm1(i ,j ) = 1 ; end end end dm1 = imcrop(dm1,[Para(1 ,2 )-Para(1 ,3 ) Para(1 ,1 )-Para(1 ,3 ) 2 *Para(1 ,3 ) 2 *Para(1 ,3 )]); dm1_sobel = imcrop(dm1_sobel,[Para(1 ,2 )-Para(1 ,3 ) Para(1 ,1 )-Para(1 ,3 ) 2 *Para(1 ,3 ) 2 *Para(1 ,3 )]); figure ; imshow(dm1_sobel);hold on;[H,Theta,Rho] = hough(dm1_sobel); P = houghpeaks(H,2 ,'threshold' ,ceil (0.1 *max (H(:)))); lines = houghlines(dm1_sobel,Theta,Rho,P,'FillGap' ,5 ,'MinLength' ,7 ); for k = 1 :length (lines) xy = [lines(k).point1; lines(k).point2]; plot (xy(:,1 ),xy(:,2 ),'LineWidth' ,2 ,'Color' ,'g' ); end
几何校正 根据 Data Matrix 码 的表示方法,我们需要将图像根据定位到的直线进行旋转 ,使得直线呈“L”型。
此外,为了获得纯净的二维码图像,我们再根据二维码边长进一步裁剪图像,然后再对原图像进行二值化。
同样地,测试得到良好的阈值:
Image dm1dm2dm3Threshold 0.23 0.34 0.60
矫正缺陷 :由于实验图像基本都是从正面垂直拍摄 的,因此获取到的图像除了旋转要求外无需再做处理。但是实际中往往需要进行真正的 几何校正 ,相当于将倾斜拍摄的二维码也进行转正。这里我们并没有做进一步的优化。
数据读取算法设计 得益于 DM码 简单的编码方式,我们只需对获取到的正面二值化 DM码图像 中黑色和白色方块进行扫描存储 即可。
算法步骤 通过检测到的直线长度计算方格的边长a = l e n / ( n u m s + 2 ) a=len/(nums+2) a = l e n / ( n u m s + 2 ) l e n len l e n n u m s nums n u m s 创建一个DM码的数据存储矩阵D a t a Data D a t a ( n u m s + 2 ) × ( n u m s + 2 ) (nums+2)\times (nums+2) ( n u m s + 2 ) × ( n u m s + 2 ) 初始化为全0 ; 创建一个和方格大小(a × a a\times a a × a C u b e = [ 1 ⋯ 1 ⋮ ⋮ 1 ⋯ 1 ] Cube=\begin{bmatrix}1&\cdots&1\\\vdots&&\vdots\\1&\cdots&1\end{bmatrix} C u b e = 1 ⋮ 1 ⋯ ⋯ 1 ⋮ 1 从图像的左上角G 11 = [ f ( x 1 , y 1 ) ⋯ f ( x 1 , y 1 + a ) ⋮ ⋮ f ( x 1 + a , y 1 ) ⋯ f ( x 1 + a , y 1 + a ) ] G_{11}=\begin{bmatrix}f(x_1,y_1)&\cdots&f(x_1,y_1+a)\\\vdots&&\vdots\\f(x_1+a,y_1)&\cdots&f(x_1+a,y_1+a)\end{bmatrix} G 11 = f ( x 1 , y 1 ) ⋮ f ( x 1 + a , y 1 ) ⋯ ⋯ f ( x 1 , y 1 + a ) ⋮ f ( x 1 + a , y 1 + a ) C u b e Cube C u b e 计算出结果矩阵中 的“含1量” :t m p = ∑ ( G 11 ∗ C u b e ) / a 2 tmp=\sum (G_{11}*Cube) /a^2 t m p = ∑ ( G 11 ∗ C u b e ) / a 2 如果含1量大于给定阈值T T T D a t a [ 1 , 1 ] = 1 Data[1,1] = 1 D a t a [ 1 , 1 ] = 1 滚动到下一个方格G 12 , G 13 , ⋯ G_{12},G_{13},\cdots G 12 , G 13 , ⋯ 截取D a t a Data D a t a n u m s × n u m s nums\times nums n u m s × n u m s 同样地,测试得到良好的阈值:
Image dm1dm2dm3Threshold 0.400 0.350 0.332
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 len = sqrt ((lines(1 ).point1(1 )-lines(1 ).point2(1 ))^2 +(lines(1 ).point1(2 )-lines(1 ).point2(2 ))^2 ); dm1 = imcomplement(dm1); dm1 = imrotate(dm1,lines(1 ).theta); dm1 = imcomplement(dm1); dm1 = im2bw(dm1,0.23 ); dm1 = imcrop(dm1,[size (dm1,1 )/2 -len/2 size (dm1,2 )/2 -len/2 len len]); figure ; imshow(dm1);a = round (len/12 ); cube = ones (a,a); result = zeros (12 ,12 ); for i = 1 :a:size (dm1,1 )-a for j = 1 :a:size (dm1,2 )-a tmp = dm1(i :i +a-1 ,j :j +a-1 ).*cube; if sum(tmp(:))/(a*a) > 0.4 result((i -1 )/a+1 ,(j -1 )/a+1 ) = 1 ; end end end result = result(2 :11 ,2 :11 ); figure ;imagesc(result);axis equal,axis tight,axis off
算法缺陷 本算法只能处理图像毫无污染 的 DM 码,没有使用到 DM码 自身的纠错能力; 本算法利用了 DM码 中方格个数n u m s × n u m s nums\times nums n u m s × n u m s 先验知识 ,不具有普适性; 本算法需要对每一个图像的阈值单独人工选取 ,不具备可靠性和通用性; 本算法需要遍历每一个像素点,时间复杂度 是O ( l e n 2 ) O(len^2) O ( l e n 2 ) 空间复杂度 是O ( a 2 ) O(a^2) O ( a 2 ) 结果与思考 图片 二维码中心坐标 二维码角度 DMO1.bmp(634, 696) -82 DM02.bmp(434, 323) -90 DM03.bmp(633, 695) -82
参考 Hough 圆变换----Matlab实现|CSDN matlab hough检测直线工具箱|CSDN Data Matrix二维码编码原理及其识别技术|CSDN