图网络浅学Ⅱ：通用框架GraphGPS

前言

在之前的博客中，我们系统的介绍了传统的图神经网络，特别是以图卷积神经网络为主的经典模型。并且给出了以消息传递机制为核心的图学习通用框架 MPNN。

图网络浅学：图神经网络及其发展

https://qslie.top/posts/193ebd1a

本文章将在此基础上介绍图深度学习中的其他问题和困境，此外更进一步介绍Transformer模型与图学习的结合，描述了论文GraphGPS，所提出的 Graph Transformer 新的通用范式。

图学习的困境

Over-Smoothing

Over-Squashing

图神经网络的困境，用微分几何和代数拓扑解决_澎湃号·湃客_澎湃新闻-The Paper

ICLR 2022(得分8/8/8/10)|| 通过曲率理解图上的over-squashing和Bottleneck的问题 - 知乎 (zhihu.com)

Over-Globalizing

图注意力网络 GTs

鉴于 Transformer 类模型在 NLP 乃至 CV 领域已经获得了一定的成功和突破，一个很自然的想法也就油然而生，那就是将 Transformer 带到 Graph 领域中来。这或许能够解决 MPNNs（消息传递范式下的GNNs）的过平滑（over-smoothing） 和 过挤压（over-squashing）问题——这与NLP中的梯度消失和长期依赖问题是类似的。

位置编码 PE

Fully-connected Graph Transformer 首次提出用图拉普拉斯矩阵的特征向量作为节点的位置编码 (positional encoding, PE) 从而在 Transformer 架构下引入了对图节点位置信息的感知。

SAN 在此基础上，实现了不变的特征向量聚合方案，并且引入条件注意力来处理图的实边和虚边。

Graphormer 提出使用成对的图距离(或3D距离)来定义相对位置编码，在大型分子基准上取得了出色的成功。

GraphiT 利用扩散核（diffusion kernel）来构建位置编码。

GraphTrans 首次提出使用混合的架构，在图全连接之前先过一个 MPNN 层。

其他 GTs 架构: SAT, EGT, GRPE, tec.

子图token法

$$\mathbf{x}^{\prime}_i = h_{\mathbf{\Theta}} \left( (1 + \epsilon) \cdot         \mathbf{x}_i + \sum_{j \in \mathcal{N}(i)} \mathbf{x}_j \right)$$

GraphGPS

📃Paper: Recipe for a General, Powerful, Scalable Graph Transformer
🔔Github: https://github.com/rampasek/GraphGPS

GraphGPS 的主要贡献如下：

• 提供了一个通用General、强大Powerful、规模可变Scalable 的Graph Transformer构建方案 GraphGPS；
• 对不同的 位置编码PE 和 结构编码SE 方案给出了一个清晰的定义，并把它们分为 local, global 和 relative三种类型；
• 利用 linear global attention 有效地降低了计算复杂度，从而让 GTs 可应用于更大规模的图结构中；
• 在多个数据集上验证了提出方法的有效性。

1-WL测试

1-Weisfeiler-Leman test (1-WL) 是一种图同构测试方法，属于图同构判定的一系列Weisfeiler-Leman（WL）算法中最基础的形式。该方法由Weisfeiler 和 Leman 于1968年提出，最初用于图的着色问题，后来发展成为检验两个图是否同构的有力工具。

1-WL 测试的基本思想是通过顶点的邻居信息来更新顶点的标签（或颜色），从而逐步区分不同的顶点和图结构。如果设$\boldsymbol L_v$ 是节点$v$ 的标签，那么它的第$k$ 步更新可以写作：

$$\mathbf{L}_{v}^{(k+1)}=\text{Hash}\left(\mathbf{L}_v^{(l)},\{\mathbf{L}_u^{(l)}\mid{\forall}u{\in}N(v)\}\right)\;$$

如果两个图经过1-WL算法，通过不断迭代到停止条件（通常是标签值不再变化）后，这两个图对应的所有节点的标签相同，则两个图可能是同构的（但不是充分条件）。

不难发现，这与一个 1-hop 的 MPNNs （的聚合部分）是很类似的。

虽然1-WL测试在很多情况下能够有效地区分不同的图，但它也存在一些局限性：

1. 非充分条件：
   即使两个图的1-WL标签序列相同，它们也不一定是同构的。因此，1-WL测试有时会产生假同构。
2. 对某些图结构的无效性：
   对于某些特殊的图结构（如强正则图），1-WL测试可能无法区分它们。

MPNNs 实际上也保留了这样的特点。

---

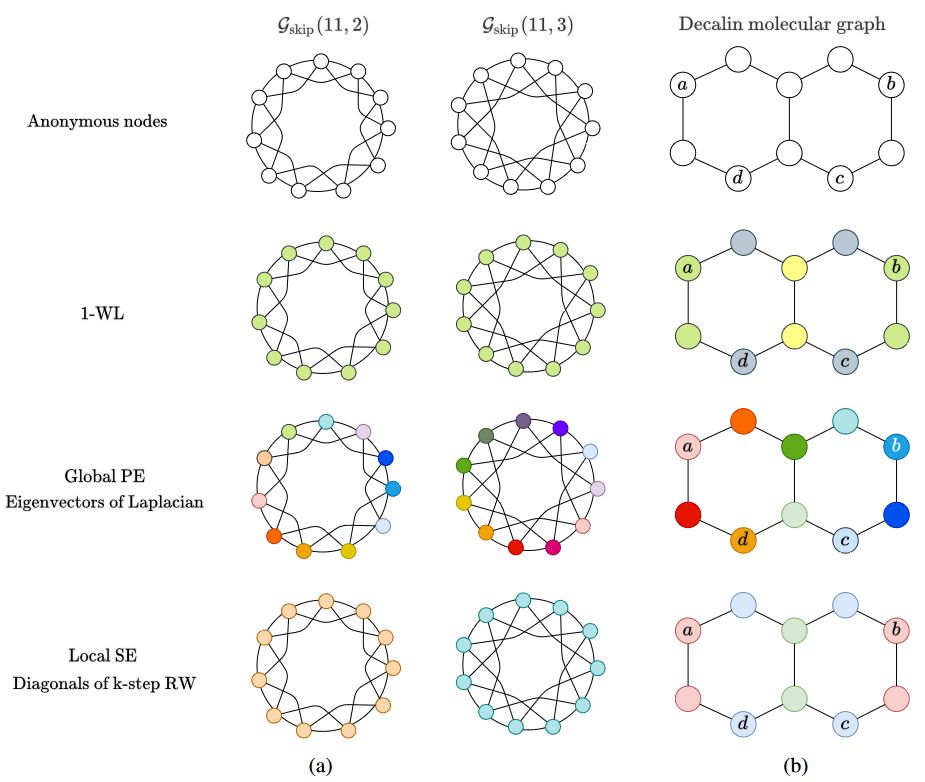
如上图(a)所示，当我们使用 1-WL来处理两个明显异构(non-isomorphic) 的 环形跳跃连接（Circular Skip Link, CSL）图$\mathcal G_{\text{skip}}(11,2)$ 和$\mathcal G_{\text{skip}}(11,3)$ 时，二者均把它们视为是同构图了（MPNN也是同样的结果）。而如果采用 Global PE 或 Local SE 来进行测试，则可以成功把二者区分开来（节点的颜色不同）。

同样地，如(b)所示，考虑双环结构的十氢化萘分子（Decalin molecule），在图中节点a和节点b是同构的，节点c和节点d是同构的。特别地，如果任务是识别节点集$(a,d)$ 和$(b,d)$ 之间的潜在链接时，1-WL/MPNN 甚至 Local SE 的方案就失效了，此时仅有 Global PE 能够胜任该任务。

最终作者得到一个重要结论：如果不将位置编码 (positional encoding, PE) 和 结构编码 (structural encoding, SE) 用于增强和修改MPNNs的学习任务，那么MPNNs将不能保证能获得足够好的信息，从而减弱了其学习能力。

PE/SE

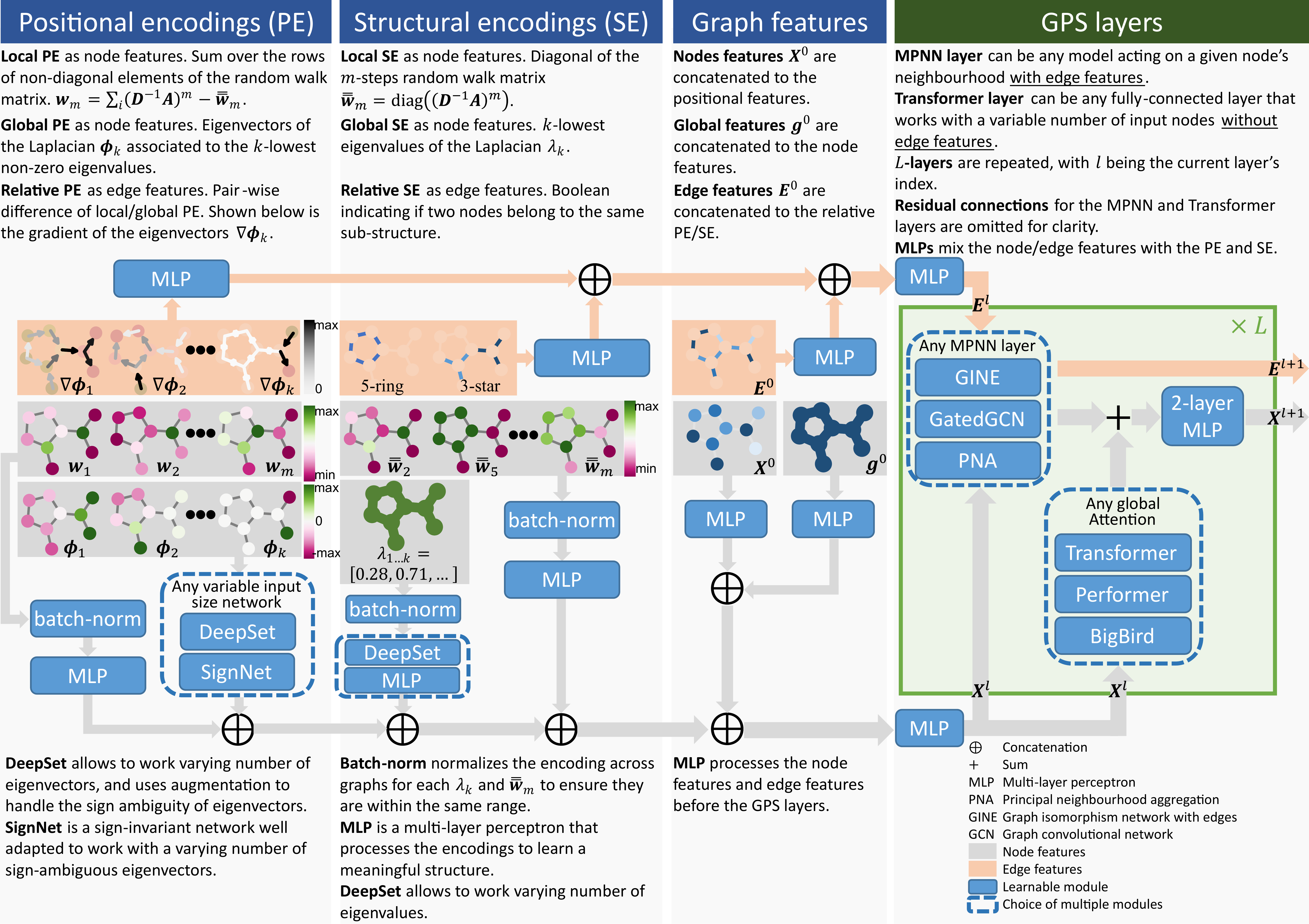
位置编码 (positional encoding, PE) 和 结构编码 (structural encoding, SE) 是驱动 Graph Transformer 能够高效运行和应用的重要因素。因此，更好地理解和组织它们有助于构建更模块化的体系结构。

• PE: 用于提供给定节点在空间中的位置信息。因此，当一个图或子图中的两个节点彼此接近时，它们的PE也应该接近。
• SE: 旨在提供图或子图的结构性 embedding，以帮助提高图神经网络的表达性和泛化性。因此，当两个节点共享相似的子图时，或者当两个图相似时，它们的SE也应该接近。

PE/SE 的分类

如上表所示，GraphGPS 具体将 PE/SE 分为 局部local, 全局global 和 关系型relative 三种类型。对它们的中文描述可参见：GraphGPS论文解读 - 知乎

GPS Layer

在以往的工作中，参考了计算机视觉领域中，在 Transformer层之前堆叠多个 CNN 层的做法，例如GraphTrans，会首先堆叠几层MPNN，将它们置于Transformer层之前，从而获得图信息的表达。

然而，受限于传统 MPNN 过平滑、过挤压，以及和 1-WL 一样的信息损失问题，即使是加入了 PE/SE 机制也很难缓解这系列问题带来的瓶颈。为此，GraphGPS 给出的解决方案是融合 MPNN 和 Transformer 而不是单纯的拼接它们。一个 GPS Layer 的结构如下图所示：

$$\begin{aligned} \mathbf{X}_{\mathsf{MMPN}}^{\ell+1}, \mathbf{E}^{\ell+1}&=\text{MMPN}^{\ell}(\mathbf X^{\ell},\mathbf{E}^{\ell},\mathbf{A})\\ \mathbf{X}_{\mathsf{Tf}}^{\ell+1}&=\text{Attn}^{\ell}(\mathbf X^{\ell})\\ \mathbf{X}^{\ell+1}&=\text{MLP}^{\ell}(\mathbf{X}_{\mathsf{MMPN}}^{\ell+1}+\mathbf{X}_{\mathsf{Tf}}^{\ell+1}) \end{aligned}$$

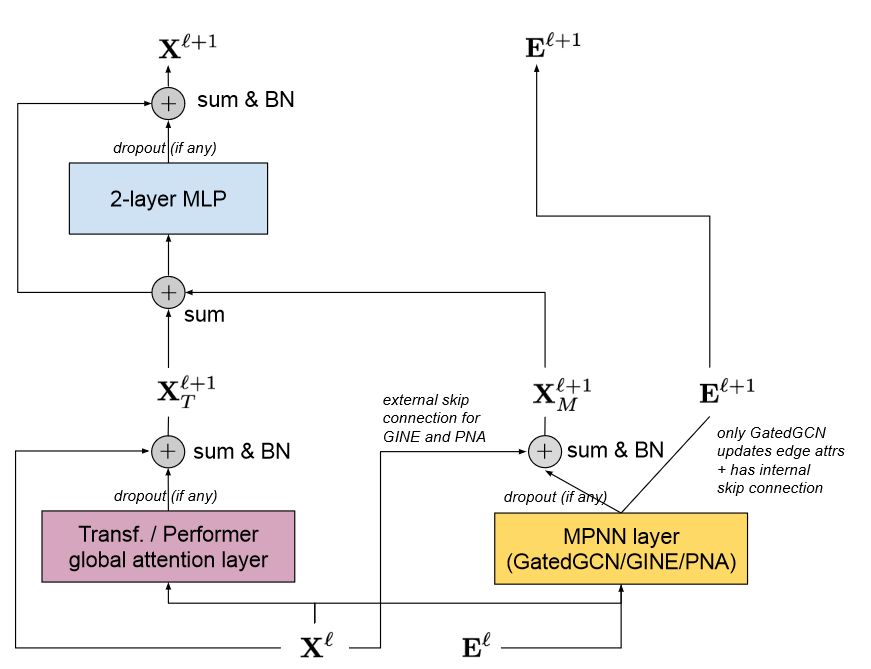
其中，$\mathbf X^{\ell}$ 表示第$\ell$ 层的节点特征，一边通过全连接的全局注意力层（也就是任意两两节点都有一个虚边），另一边和第$\ell$ 层的实边（即真实的边特征）$\mathbf E^{\ell}$ 一起通过局部的 MPNN 层，两边都使用残差连接的方式，然后合并起来过一个用$\operatorname{ReLU}$ 为激活函数的 2-layer MLP 最终得到下一层的节点特征表示。

---

用户可以 PE/SE、Transformer、MPNN 以及最后预测头方案选取的不同，而遵循以上框架得到不同的模型，这是 GraphGPS 模块化（modularity）的体现。

规模可变性（Scalability） 是通过将模型的计算复杂度降低到$O(N +E)$ 来实现的，其中$N$ 和$E$ 分别是节点和边的数量（忽略PE/SE阶段比如分解拉普拉斯矩阵等操作的计算开销）。其中，通过将PE/SE限制在真实节点和边上，并在global attention层不让 Real Edge 纳入计算，还可以避免完整的平方级的注意力矩阵计算，使用Linear Transformer 以降低节点计算的复杂度为$O(N)$；而 MPNN 则是$O(E)$。

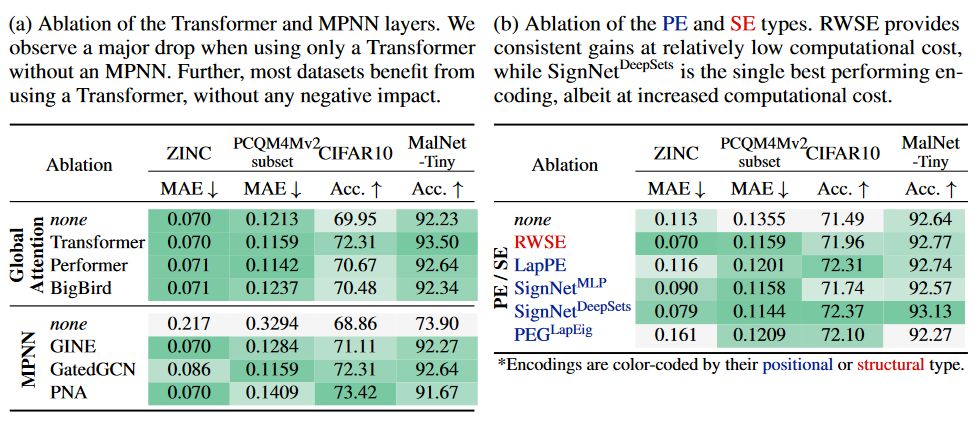
消融实验

作者对不同的Transformer层和MPNN层进行了消融实验，结果表明Transformer结构对提升效果有明显作用，其中Linear Transformer结构（Performer、BigBird）也均有提升效果，但是和普通的 $O(N^2)$  的 transformer 还有一定差距。另外，不同的MPNN结构（GINE、GateGCN、PNA等）对实验结果也有明显的提升。

另一方面，作者还评估了各种PE/SE方案的效果，发现它们通常有利于下游任务。但是不同编码的方式的效果非常依赖于数据集，随机游走结构编码(RWSE)更有利于分子数据，而拉普拉斯特征向量编码(LapPE)更有利于图像超像素。然而，使用带有DeepSets编码的SignNet作为处理LapPE的一种改进方法，似乎在多个任务中都有提升效果。

参考

1. Recipe for a General, Powerful, Scalable Graph Transformer (arxiv.org)
2. GraphGPS论文解读：Recipe for a General, Powerful, Scalable Graph Transformer - 知乎