Attention Free 在本站文章《注意力机制及其线性化之路 》中我们简单梳理了注意力机制的原理、不同评分函数的设计以及走在科研道路上的线性化之路。归根结底,各种 Attention 的变体,其本质都是为了对于给定的输入查询q q q k k k 注意力权重 ,然后将k k k v v v
所以,我们其实也没必要将注意力计算的方式固定在缩放点积注意力上。只要我们能够以比 Transformer 更低的复杂度比较有效的计算出注意力权值,那么便可以解决Transformer带来的高复杂度问题。因此,由Apple公司提出的一种新型的神经网络模型Attention Free Transformer (AFT) 就聚焦于这一点,尝试设计一个高效的权值计算方式。
AFT的论文中提出了四个不同的Attention Free的计算方式,分别是AFT-full,AFT-local,AFT-simple和AFT-conv,下面我们来分别介绍他们。
AFT-full AFT-full 是 AFT 的原始形态,它首先也是和自注意力机制一样先将输入通过三个线性层得到Q,K,V.
学习 Transformer-XL 引入了相对位置编码 w t , t ′ w_{t,t'} w t , t ′ 标量 参数并且对 multi-head 是共享的,用来表示第t t t t ′ t' t ′
然后直接就对加入位置编码偏置 的K t ′ + w t , t ′ \mathbf K_{t^{\prime}}+w_{t, t^{\prime}} K t ′ + w t , t ′ s o f t m a x \mathrm{softmax} softmax v v v
Weighted ( K t ′ ) = exp ( K t ′ + w t , t ′ ) ∑ t ′ = 1 T exp ( K t ′ + w t , t ′ ) \text{Weighted}(\mathbf K_{t^{\prime}})=\frac{\exp \left(\mathbf K_{t^{\prime}}+w_{t, t^{\prime}}\right)}{\sum_{t^{\prime}=1}^T \exp \left(\mathbf K_{t^{\prime}}+w_{t, t^{\prime}}\right)} Weighted ( K t ′ ) = ∑ t ′ = 1 T exp ( K t ′ + w t , t ′ ) exp ( K t ′ + w t , t ′ )
开始给v v v
∑ t ′ = 1 T Weighted ( K t ′ ) ⊙ V t ′ \sum_{t'=1}^{T}\text{Weighted}(\mathbf K_{t^{\prime}})\;\odot\;\mathbf V_{t'} t ′ = 1 ∑ T Weighted ( K t ′ ) ⊙ V t ′
最后再和使用 Sigmoid 非线性化后的Q t {\bf Q}_t Q t Y t {\bf Y}_t Y t
Y t = σ q ( Q t ) ⊙ ∑ t ′ = 1 T exp ( K t ′ + w t , t ′ ) ⊙ V t ′ ∑ t ′ = 1 T exp ( K t ′ + w t , t ′ ) \mathbf Y_t=\sigma_q\left(\mathbf Q_t\right) \odot \frac{\sum_{t^{\prime}=1}^T \exp \left(\mathbf K_{t^{\prime}}+w_{t, t^{\prime}}\right) \odot \mathbf V_{t^{\prime}}}{\sum_{t^{\prime}=1}^T \exp \left(\mathbf K_{t^{\prime}}+w_{t, t^{\prime}}\right)} Y t = σ q ( Q t ) ⊙ ∑ t ′ = 1 T exp ( K t ′ + w t , t ′ ) ∑ t ′ = 1 T exp ( K t ′ + w t , t ′ ) ⊙ V t ′
实际上,如果把σ q ( Q t ) \sigma_q\left(\mathbf Q_t\right) σ q ( Q t ) v v v q , k q,k q , k
AFT-local AFT-full 的实现难点在于∑ t ′ = 1 T exp ( K t ′ + w t , t ′ ) ⊙ V t ′ \sum_{t^{\prime}=1}^T \exp \left(\mathbf K_{t^{\prime}}+w_{t, t^{\prime}}\right) \odot \mathbf V_{t^{\prime}} ∑ t ′ = 1 T exp ( K t ′ + w t , t ′ ) ⊙ V t ′
exp ( W ) × ( exp ( K ) ⊙ V ) \exp(\mathbf W)\times(\exp(\mathbf K)\odot\mathbf V) exp ( W ) × ( exp ( K ) ⊙ V )
实际上不难得出它的复杂度和 Transformer 一样也是O ( T 2 d ) \mathcal O(T^2d) O ( T 2 d ) w t , : \boldsymbol w_{t,:} w t , : s < T s\lt T s < T
w t , t ′ = { w t , t ′ , if ∣ t − t ′ ∣ < s 0 , otherwise w_{t, t^{\prime}}= \begin{cases}w_{t, t^{\prime}}, & \text { if }\left|t-t^{\prime}\right|<s \\ 0, & \text { otherwise }\end{cases} w t , t ′ = { w t , t ′ , 0 , if ∣ t − t ′ ∣ < s otherwise
这也就是 AFT-local。
🤔这不就类似于 Local Attention 吗?
AFT-conv 作者进一步扩展到局部权重共享,即卷积方法上,用以使用视觉任务。具体来说,将w \boldsymbol w w K \bf K K
Y t i = σ q ( Q t i ) ⊙ conv ( exp ( K i ) ⊙ V i , exp ( w i ) − 1 ) + ∑ t ′ = 1 T exp ( K t ′ i ) ⊙ V t ′ i conv ( exp ( K i ) , exp ( w i ) − 1 ) + ∑ t ′ = 1 T exp ( K t ′ i ) \mathbf Y_t^i=\sigma_q\left(\mathbf Q_t^i\right) \odot \frac{\operatorname{conv}\left(\exp \left(\mathbf K^i\right) \odot \mathbf V^i, \exp \left(\boldsymbol w^i\right)-1\right)+\sum_{t^{\prime}=1}^T \exp \left(\mathbf K_{t^{\prime}}^i\right) \odot \mathbf V_{t^{\prime}}^i}{\operatorname{conv}\left(\exp \left(\mathbf K^i\right), \exp \left(\boldsymbol w^i\right)-1\right)+\sum_{t^{\prime}=1}^T \exp \left(\mathbf K_{t^{\prime}}^i\right)} Y t i = σ q ( Q t i ) ⊙ conv ( exp ( K i ) , exp ( w i ) − 1 ) + ∑ t ′ = 1 T exp ( K t ′ i ) conv ( exp ( K i ) ⊙ V i , exp ( w i ) − 1 ) + ∑ t ′ = 1 T exp ( K t ′ i ) ⊙ V t ′ i
这里的上标i i i i i i i i i
AFT-simple 如果去掉位置编码的话,我们会有形如Y = σ q ( Q ) ⊙ ∑ ( softmax ( K ) ⊙ V ) \mathbf Y=\sigma_q(\mathbf Q)\odot\sum\big(\text{softmax}(\mathbf K)\odot\mathbf V\big) Y = σ q ( Q ) ⊙ ∑ ( softmax ( K ) ⊙ V ) 线性注意力 进化之路的思想如出一辙。这便是AFT的极简版本。在这个版本中,上下文缩减进一步简化为逐元素操作和全局池化。
RWKV-4 RWKV(读作 RWaKuV)是一种具有 GPT 级大型语言模型(LLM)性能的RNN ,也可以像 GPT Transformer 一样直接训练(可并行化 )。项目最初由彭博(Bo Peng ,BlinkDL)提出,随着项目被外界关注,RWKV 项目逐渐发展成一个开源社区。
RWKV 模型架构有 RWKV-4、RWKV-5(代号 Eagle)、RWKV-6(代号 Finch) 三个正式版本 ,更早以前的 RWKV 1/2/3 为实验版本。RWKV-4 是 RWKV 模型的首个正式版本 ,论文由 RWKV 作者彭博和 RWKV 社区共同完成,初次发表于 2023 年 5 月 22 日。
RWKV 架构的名称来源于时间混合 和通道混合 块中使用的四个主要模型参数,分别如下:
R R R Receptance ,作为过去信息的接受程度的接受向量W W W Weight ,位置权重衰减向量,可训练的模型参数K K K Key )是类似于传统注意力中 K K K V V V Value )是类似于传统注意力中 V V V
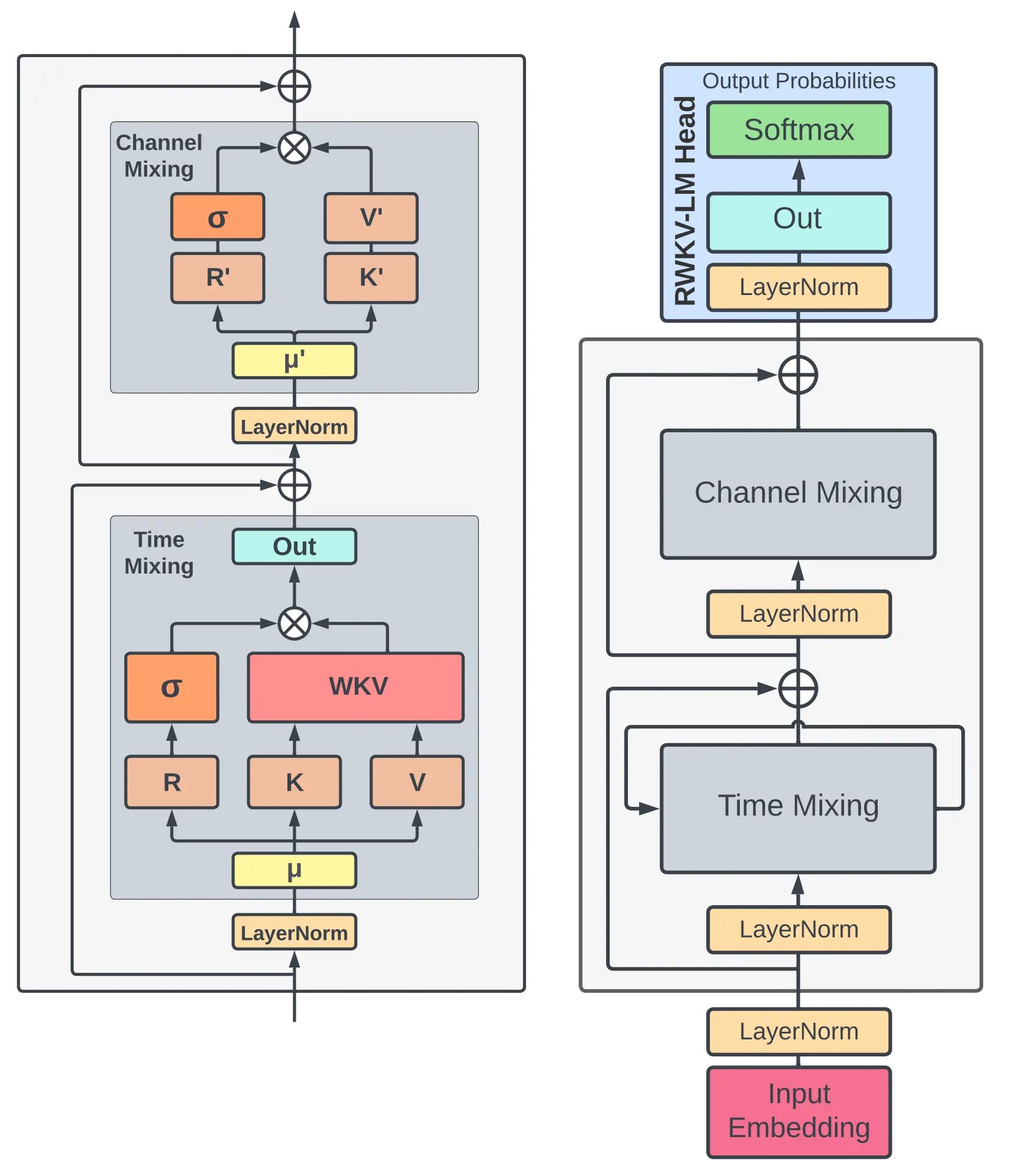
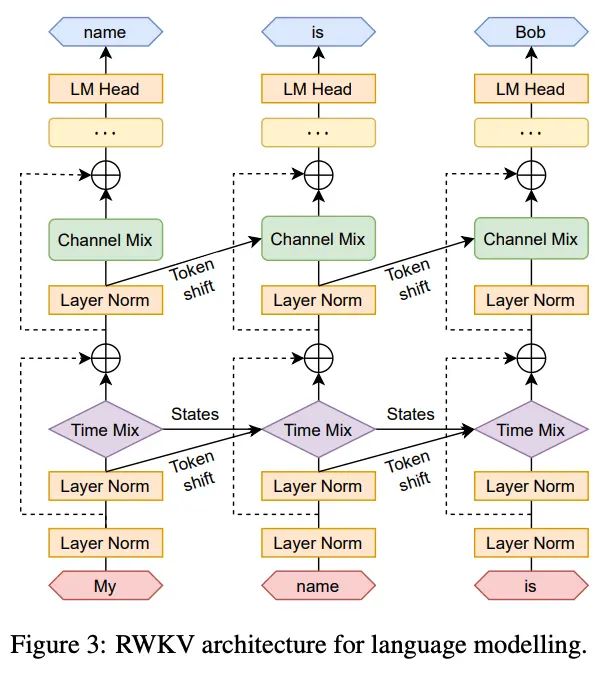
上图是 RWKV-V4 论文中的模型架构概览,其中:
左侧:RWKV-V4 的 time-mixing 和 channel-mixing 模块 右侧:RWKV-V4 的语言建模流程 Token Shift 与 Transformer 的 Self-attention 类似,RWKV 中的两个关键 mixing 模块也运用了三个从原始输入投影而来的变量(R , K , V R,K,V R , K , V R ′ , K ′ R',K' R ′ , K ′ 这些变量除了由当前时间步t t t t − 1 t-1 t − 1 (在LLM中就是当前读到的单词的 token)。
类似于 RNN 的遗忘门操作,设立了固定的参数μ \mu μ
r t = W r ⋅ ( μ r ⊙ x t + ( 1 − μ r ) ⊙ x t − 1 ) , k t = W k ⋅ ( μ k ⊙ x t + ( 1 − μ k ) ⊙ x t − 1 ) , v t = W v ⋅ ( μ v ⊙ x t + ( 1 − μ v ) ⊙ x t − 1 ) r t ′ = W r ⋅ ( μ r ′ ⊙ x t + ( 1 − μ r ′ ) ⊙ x t − 1 ) , k t ′ = W k ⋅ ( μ k ′ ⊙ x t + ( 1 − μ k ′ ) ⊙ x t − 1 ) \begin{aligned} \boldsymbol{r_{t}} & =\mathbf W_{r} \cdot( \mu_{r} \odot\boldsymbol x_{t}+( 1-\mu_{r} ) \odot\boldsymbol x_{t-1} ), \\ \boldsymbol{k_{t}} & =\mathbf W_{k} \cdot( \mu_{k} \odot\boldsymbol x_{t}+( 1-\mu_{k} ) \odot\boldsymbol x_{t-1} ), \\ \boldsymbol{v_{t}} & =\mathbf W_{v} \cdot( \mu_{v} \odot\boldsymbol x_{t}+( 1-\mu_{v} ) \odot\boldsymbol x_{t-1} ) \\\\ \boldsymbol{r_{t}'} & =\mathbf W_{r} \cdot( \mu_{r}' \odot\boldsymbol x_{t}+( 1-\mu_{r}' ) \odot\boldsymbol x_{t-1} ), \\ \boldsymbol{k_{t}'} & =\mathbf W_{k} \cdot( \mu_{k}' \odot\boldsymbol x_{t}+( 1-\mu_{k}' ) \odot\boldsymbol x_{t-1} ) \end{aligned} r t k t v t r t ′ k t ′ = W r ⋅ ( μ r ⊙ x t + ( 1 − μ r ) ⊙ x t − 1 ) , = W k ⋅ ( μ k ⊙ x t + ( 1 − μ k ) ⊙ x t − 1 ) , = W v ⋅ ( μ v ⊙ x t + ( 1 − μ v ) ⊙ x t − 1 ) = W r ⋅ ( μ r ′ ⊙ x t + ( 1 − μ r ′ ) ⊙ x t − 1 ) , = W k ⋅ ( μ k ′ ⊙ x t + ( 1 − μ k ′ ) ⊙ x t − 1 )
NOTE: Channel mixing 模块的r t ′ \boldsymbol{r}_t' r t ′ k t ′ \boldsymbol{k}_t' k t ′ x t \boldsymbol{x}_t x t x t \boldsymbol{x}_t x t
Time Mixing Time mixing 模块主要是受理所有输入数据并捕捉到 token 之间的时间依赖关系。RWKV 中则是借鉴了 AFT 的方法(说白了就是利用一种带位置偏置的线性注意力方法)来捕捉这种关系,然后输出隐变量。
值得注意的是,RWKV 中对位置偏置{ w t , i } ∈ R T × T \{w_{t,i}\}\in\mathbb R^{T\times T} { w t , i } ∈ R T × T w ∈ R ( ≥ 0 ) w\in\mathbb R_{(\geq 0)} w ∈ R ( ≥ 0 )
将其乘以当前时间步t t t token 和之前的时间步i i i
w t , i = − ( t − i ) w w_{t,i}=-(t-i)w w t , i = − ( t − i ) w
此外,为了避免位置偏置W \bf W W 潜在退化 ,RWKV还多引入一个单独关注当前 token 的向量。对前t − 1 t-1 t − 1
最终 RWKV 延续了将注意力以RNN推理的思路,给出了从第一个时间步(i = 1 i=1 i = 1 w k v t \boldsymbol{wkv}_t wkv t
w k v t = ∑ i = 1 t − 1 exp ( k i − ( t − i ) w ) ⊙ v i + exp ( k t + u ) ⊙ v i ∑ i = 1 t − 1 exp ( k i − ( t − i ) w ) + exp ( k t + u ) \boldsymbol{wkv}_t=\frac{\sum_{i=1}^{t-1} \exp \left(\boldsymbol k_{i}-(t-i)w\right) \odot \boldsymbol v_{i}+\exp(\boldsymbol k_t+u)\odot \boldsymbol v_{i}}{\sum_{i=1}^{t-1} \exp \left(\boldsymbol k_{i}-(t-i)w\right)+\exp(\boldsymbol k_t+u)} wkv t = ∑ i = 1 t − 1 exp ( k i − ( t − i ) w ) + exp ( k t + u ) ∑ i = 1 t − 1 exp ( k i − ( t − i ) w ) ⊙ v i + exp ( k t + u ) ⊙ v i
和 AFT 一样,要得到 Time mixing 的输出,只需要将w k v t \boldsymbol{wkv}_t wkv t σ ( r t ) \sigma(\boldsymbol r_t) σ ( r t )
o t = W o ( σ ( r t ) ⊙ w k v t ) \boldsymbol o_t=\mathbf W_o\big(\sigma(\boldsymbol r_t)\odot \boldsymbol{wkv}_t\big) o t = W o ( σ ( r t ) ⊙ wkv t )
Channel Mixing Channel mixing 模块因为在 Time mixing 模块之后使用,该过程对拿到的输入重新做了线性投影,并且引入了非线性激活,这些操作充分让每一个 token 内部的 d_model 维向量数据充分混合。
o t ′ = σ ( r t ′ ) ⊙ ( W v ′ ⋅ max ( k t ′ , 0 ) 2 ) \boldsymbol o_t'=\sigma(\boldsymbol r_t')\odot\big(\mathbf W_v'\cdot \max( \boldsymbol{k}_t',0)^2\big) o t ′ = σ ( r t ′ ) ⊙ ( W v ′ ⋅ max ( k t ′ , 0 ) 2 )
其中max ( ⋅ , 0 ) 2 \max(\cdot,0)^2 max ( ⋅ , 0 ) 2
Conclusion RWKV 的优点:结合了 Transformer 和 RNN 的优势,训练时能够像 Transformer 那样并行计算,推理时又能像 RNN 那样高效。尤其是后者,对于降低模型成本,尤其是在端侧部署有重要意义。另外 RWKV 的计算量与上下文长度无关 ,对于更长的上下文可能有更好的扩展性。
RWKV 的缺点:和 RNN 一样,历史信息是靠隐状态(WKV)来记忆的,对于长距离历史信息的记忆不如 Transformer。这个很容易理解,因为 RWKV 的历史信息是存在一个向量里,时间越久衰减就越厉害,与 full attention 比自然是有局限性的。这个局限性也使得 prompt engineering 对 RWKV 更加重要 。与 Transformer 相比,由于 RWKV 对很长的上下文记忆能力有限,如何设计提示词对模型的性能会有很大影响。
RWKV-5 RWKV-5 是 RWKV-4 架构的改良版本,版本代号“Eagle(鹰)”。
RWKV-5 和 RWKV-6 这两个架构在同一篇论文 《Eagle and Finch: RWKV with Matrix-Valued States and Dynamic Recurrence》 中发布。
该论文初次发表于 2024 年 4 月 9 日。同年 10 月,RWKV 5/6 架构论文被 LLM 领域顶级会议 COLM 2024 收录。
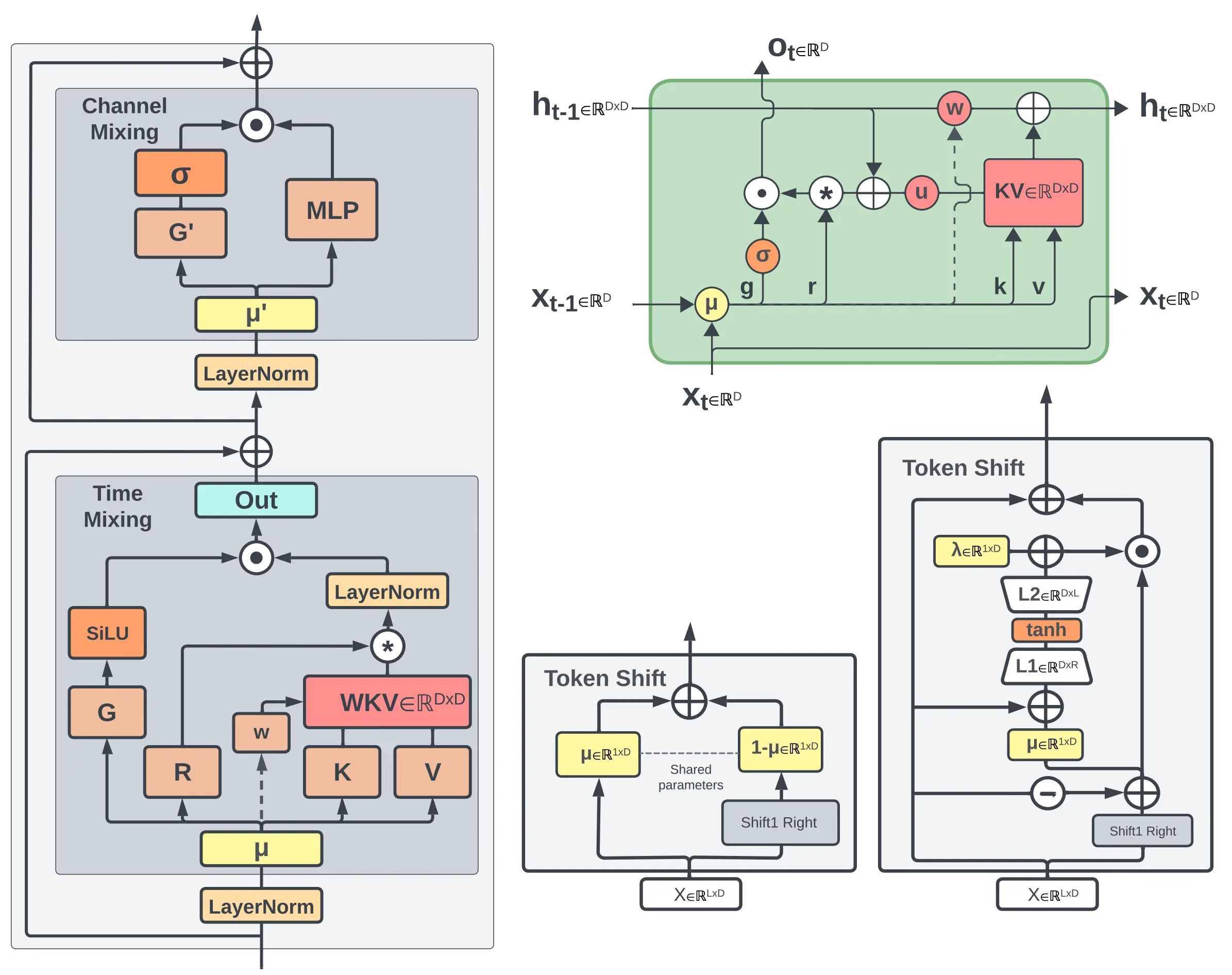
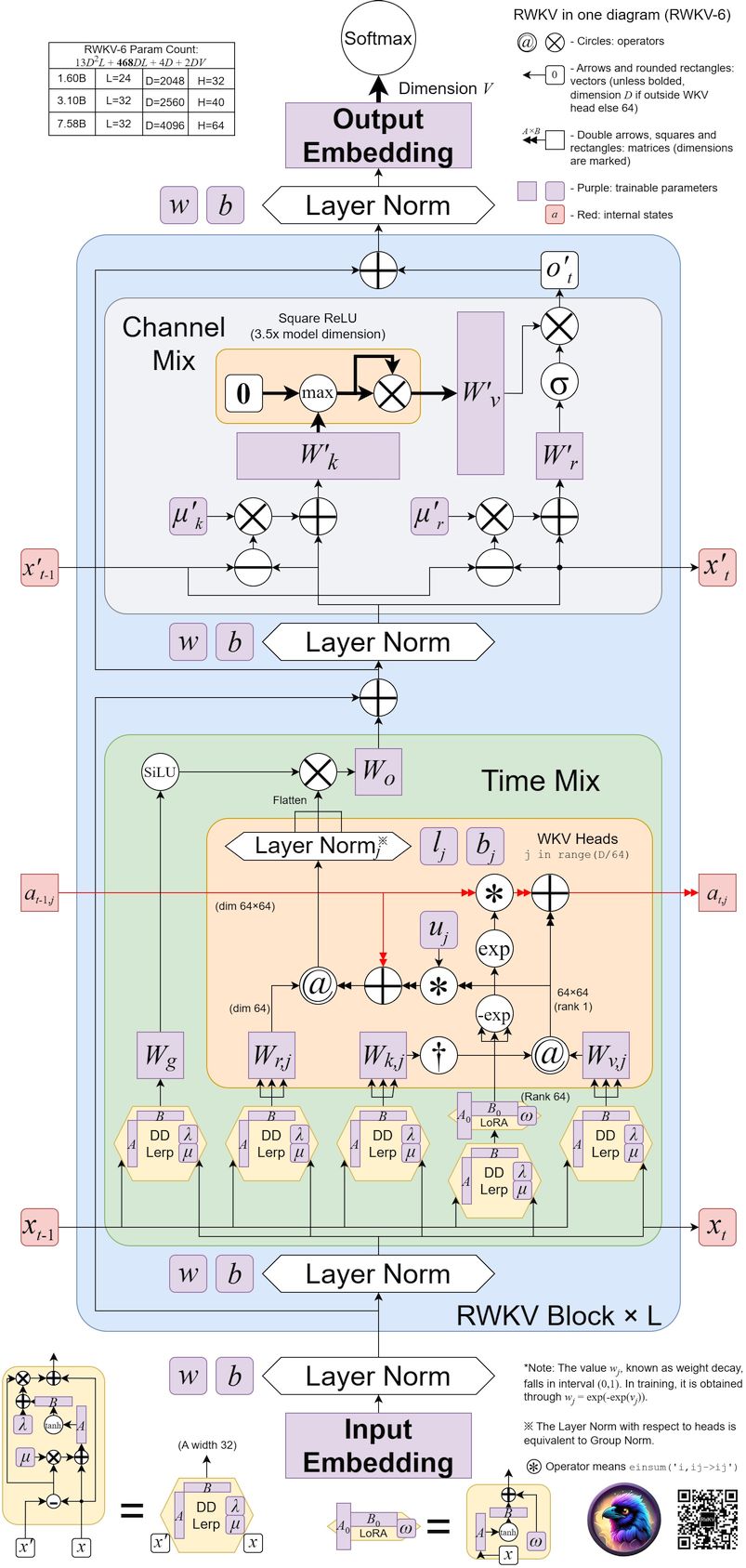
上图是论文中 RWKV 5/6 的架构概览,其中:
左侧:RWKV 的 time-mixing 和 channel-mixing 模块 右上角:作为 RNN 单元时的 RWKV time-mixing 模块,虚线箭头表示 RWKV-V6 架构的连接,但在 RWKV-5 中不存在 底部的中间:前向传播模式下 RWKV-5 time-mixing 的 token-shift 模块 右下角:前向传播模式下 RWKV-6 time-mixing 的 token-shift 模块 相对 RWKV-4, RWKV-5 的最重点改动在于引入了多头的 、基于矩阵值的状态(state) ,即论文中的 “multi-headed matrix-valued states”。
在 RWKV-4 架构的 time mixing 计算中,u u u w w w k k k v v v D D D
t t t RWKV-4u , w , k t , v t ∈ R D u, w, k_t, v_t \in \mathbb{R}^D u , w , k t , v t ∈ R D 0 σ ( r 0 ) ⊙ u ⊙ k 0 ⊙ v 0 u ⊙ k 0 \sigma(r_0) \odot \frac{u \odot k_0 \odot v_0}{u \odot k_0} σ ( r 0 ) ⊙ u ⊙ k 0 u ⊙ k 0 ⊙ v 0 1 σ ( r 1 ) ⊙ u ⊙ k 1 ⊙ v 1 + k 0 ⊙ v 0 u ⊙ k 1 + k 0 \sigma(r_1) \odot \frac{u \odot k_1 \odot v_1 + k_0 \odot v_0}{u \odot k_1 + k_0} σ ( r 1 ) ⊙ u ⊙ k 1 + k 0 u ⊙ k 1 ⊙ v 1 + k 0 ⊙ v 0 2 σ ( r 2 ) ⊙ u ⊙ k 2 ⊙ v 2 + k 1 ⊙ v 1 + w ⊙ k 0 ⊙ v 0 u ⊙ k 2 + k 1 + w ⊙ k 0 \sigma(r_2) \odot \frac{u \odot k_2 \odot v_2 + k_1 \odot v_1 + w \odot k_0 \odot v_0}{u \odot k_2 + k_1 + w \odot k_0} σ ( r 2 ) ⊙ u ⊙ k 2 + k 1 + w ⊙ k 0 u ⊙ k 2 ⊙ v 2 + k 1 ⊙ v 1 + w ⊙ k 0 ⊙ v 0 3 σ ( r 3 ) ⊙ u ⊙ k 3 ⊙ v 3 + k 2 ⊙ v 2 + w ⊙ k 1 ⊙ v 1 + w 2 ⊙ k 0 ⊙ v 0 u ⊙ k 3 + k 2 + w ⊙ k 1 + w 2 ⊙ k 0 \sigma(r_3) \odot \frac{u \odot k_3 \odot v_3 + k_2 \odot v_2 + w \odot k_1 \odot v_1 + w^2 \odot k_0 \odot v_0}{u \odot k_3 + k_2 + w \odot k_1 + w^2 \odot k_0} σ ( r 3 ) ⊙ u ⊙ k 3 + k 2 + w ⊙ k 1 + w 2 ⊙ k 0 u ⊙ k 3 ⊙ v 3 + k 2 ⊙ v 2 + w ⊙ k 1 ⊙ v 1 + w 2 ⊙ k 0 ⊙ v 0
而 RWKV-5 则将u u u w w w 对角化 ,而k k k v v v D D D 向量 转化为维度为64 × 64 64\times64 64 × 64 矩阵 , head size 大小改为固定的 64 。
RWKV-V 的 time-mixing 时间步:
t t t Eagle (RWKV-5)diag ( u ) \text{diag}(u) diag ( u ) diag ( w ) \text{diag}(w) diag ( w ) k t k_t k t v t ∈ R 64 × 64 v_t \in \mathbb{R}^{64 \times 64} v t ∈ R 64 × 64 0 r 0 ⋅ ( diag ( u ) ⋅ k 0 ⊤ ⋅ v 0 ) r_0 \cdot (\text{diag}(u) \cdot k_0^\top \cdot v_0) r 0 ⋅ ( diag ( u ) ⋅ k 0 ⊤ ⋅ v 0 ) 1 r 1 ⋅ ( diag ( u ) ⋅ k 1 ⊤ ⋅ v 1 + k 0 ⊤ ⋅ v 0 ) r_1 \cdot (\text{diag}(u) \cdot k_1^\top \cdot v_1 + k_0^\top \cdot v_0) r 1 ⋅ ( diag ( u ) ⋅ k 1 ⊤ ⋅ v 1 + k 0 ⊤ ⋅ v 0 ) 2 r 2 ⋅ ( diag ( u ) ⋅ k 2 ⊤ ⋅ v 2 + k 1 ⊤ ⋅ v 1 + diag ( w ) ⋅ k 0 ⊤ ⋅ v 0 ) r_2 \cdot (\text{diag}(u) \cdot k_2^\top \cdot v_2 + k_1^\top \cdot v_1 + \text{diag}(w) \cdot k_0^\top \cdot v_0) r 2 ⋅ ( diag ( u ) ⋅ k 2 ⊤ ⋅ v 2 + k 1 ⊤ ⋅ v 1 + diag ( w ) ⋅ k 0 ⊤ ⋅ v 0 ) 3 r 3 ⋅ ( diag ( u ) ⋅ k 3 ⊤ ⋅ v 3 + k 2 ⊤ ⋅ v 2 + diag ( w ) ⋅ k 1 ⊤ ⋅ v 1 + diag ( w 2 ) ⋅ k 0 ⊤ ⋅ v 0 ) r_3 \cdot (\text{diag}(u) \cdot k_3^\top \cdot v_3 + k_2^\top \cdot v_2 + \text{diag}(w) \cdot k_1^\top \cdot v_1 + \text{diag}(w^2) \cdot k_0^\top \cdot v_0) r 3 ⋅ ( diag ( u ) ⋅ k 3 ⊤ ⋅ v 3 + k 2 ⊤ ⋅ v 2 + diag ( w ) ⋅ k 1 ⊤ ⋅ v 1 + diag ( w 2 ) ⋅ k 0 ⊤ ⋅ v 0 )
RWKV-5 前向传播(推理过程)的 time-mixing 计算公式:
□ t = lerp □ ( x t , x t − 1 ) W □ , □ ∈ { r , k , v , g } \square_t = \text{lerp}_{\square}(x_t, x_{t-1}) W_{\square}, \quad \square \in \{ r, k, v, g \} □ t = lerp □ ( x t , x t − 1 ) W □ , □ ∈ { r , k , v , g }
w = exp ( − exp ( ω ) ) w = \exp(-\exp(\omega)) w = exp ( − exp ( ω ))
w k v t = diag ( u ) ⋅ k t ⊤ ⋅ v t + ∑ i = 1 t − 1 diag ( w ) t − 1 − i ⋅ k i ⊤ ⋅ v i ∈ R ( D / h ) × ( D / h ) wkv_t = \text{diag}(u) \cdot k_t^\top \cdot v_t + \sum_{i=1}^{t-1} \text{diag}(w)^{t-1-i} \cdot k_i^\top \cdot v_i \in \mathbb{R}^{(D/h) \times (D/h)} w k v t = diag ( u ) ⋅ k t ⊤ ⋅ v t + i = 1 ∑ t − 1 diag ( w ) t − 1 − i ⋅ k i ⊤ ⋅ v i ∈ R ( D / h ) × ( D / h )
o t = concat ( SiLU ( g t ) ⊙ LayerNorm ( r t ⋅ w k v t ) ) W o ∈ R D o_t = \text{concat}(\text{SiLU}(g_t) \odot \text{LayerNorm}(r_t \cdot wkv_t)) W_o \in \mathbb{R}^D o t = concat ( SiLU ( g t ) ⊙ LayerNorm ( r t ⋅ w k v t )) W o ∈ R D
NOTE: RWKV-5 的 Token Shift 和 RWKV-4 类似,是一个非常简单的线性插值 (linear interpolation - lerp ),且这个线性插值是数据无关的 (data-independent),只由参数 μ \mu μ token 和前一个 token 混合到模型输入的占比。有:
lerp □ ( a , b ) = a + ( b − a ) ⊙ μ □ \text{lerp}_{\Box}(a, b) = a + (b - a) \odot \mu_{\Box} lerp □ ( a , b ) = a + ( b − a ) ⊙ μ □
其实和 RWKV-4 没区别.
通过将 RWKV-4 的向量变成矩阵,RWKV-5 的 state 计算从“基于向量”变成了“基于 64×64 的矩阵值”,即 “matrix-valued states” 。假设当前 RWKV 模型的维度是 512 ,则可以说有 512/64 = 8 个头 (八头×64 维),这就是 RWKV-5 的“多头-multi-headed” 概念。
因此,我们可以把 RWKV-5 的优化细节总结为:
消除了归一化项(RWKV-4 公式中的分母) 引入了矩阵值状态代替以往的向量值状态 引入了 Time-mixing 门控机制,即在 time-mixing 模块中添加额外的矩阵 W g W_g W g 引入了对角衰减矩阵,也就是将 u u u w w w 通过这种方式,RWKV-5 巧妙地扩大了 state 的规模,使得 RWKV 模型有更好的记忆力和模型容量。
RWKV-6
RWKV-6 则借鉴了 Low-Rank Adaptation(LoRA)的技术,将 RWKV-4/5 中静态的参数μ \mu μ
具体来说,RWKV-6 的 Token Shift 中的线性插值公式如下:
lora □ ( x ) = λ □ + tanh ( x A □ ) B □ \text{lora}_{\Box}(x) = \lambda_{\Box} + \tanh(x A_{\Box}) B_{\Box} lora □ ( x ) = λ □ + tanh ( x A □ ) B □
ddlerp □ ( a , b ) = a + ( b − a ) ⊙ lora □ ( a + ( b − a ) ⊙ μ x ) \text{ddlerp}_{\Box}(a, b) = a + (b - a) \odot \text{lora}_{\Box}(a + (b - a) \odot \mu_x) ddlerp □ ( a , b ) = a + ( b − a ) ⊙ lora □ ( a + ( b − a ) ⊙ μ x )
相对 ,RWKV-6 这种增强了数据依赖性的新型插值方法(d ata-d ependent l inear interp olation,ddlerp)有效地扩展模型的能力,每个通道分配的新旧数据量取决于当前和之前时间步骤的输入。
通俗地理解,这种动态递归机制/数据依赖性 使“重要的信息”可以有效地标记自身,以待在后续任务使用;而“不重要的信息”也可以标记自身,以减少或完全避免进入后续的数据流,从而为更重要的现有数据保留空间。
此外,如果某些信息对于特定任务没有用,那么动态递归机制可以允许这些信息预先被过滤掉。
然后,RWKV-6 也把原来的静态位置向量w t w_t w t
d t = l o r a d ( d d l e r p d ( x t , x t − 1 ) ) d_t = \mathrm{lora}_d( \mathrm{ddlerp}_d ( x_t, x_{t-1} ) ) d t = lora d ( ddlerp d ( x t , x t − 1 ))
w t = exp ( − exp ( d t ) ) w_t = \exp(-\exp(d_t)) w t = exp ( − exp ( d t ))
因此w k v t wkv_t w k v t
w k v t = d i a g ( u ) ⋅ k t T ⋅ v t + ∑ i = 1 t − 1 d i a g ( ⨀ j = 1 i − 1 w j ) ⋅ k i T ⋅ v i ∈ R ( D / h ) × ( D / h ) {wkv}_{t} = \mathrm{diag}(u)\cdot k_{t}^\mathrm{T} \cdot v_{t} + \sum_{i=1}^{t-1} \mathrm{diag}\left(\bigodot_{j=1}^{i-1}w_{j}\right) \cdot k_{i}^\mathrm{T} \cdot v_{i} \in \mathbb{R}^{(D/h) \times (D/h)} w k v t = diag ( u ) ⋅ k t T ⋅ v t + i = 1 ∑ t − 1 diag ( j = 1 ⨀ i − 1 w j ) ⋅ k i T ⋅ v i ∈ R ( D / h ) × ( D / h )
代码梳理 此处梳理的是官方给出的 RWKV-4 简化 PyTorch 版本 ,并且是 slow version 的 RNN 纯推理版本,即并没有 利用 CUDA 实现 GPU 并行加速的内容,此代码仅做推理演示使用 。
RWKV_in_150_lines.py 相关初始配置,如LM所需的 tokenizer等。其中,20B_tokenizer.json 为分词内容,在这里 下载;RWKV-4-Pile-430M-20220808-8066为RWKV-4的预训练权重,在这里 下载。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import numpy as npnp.set_printoptions(precision=4 , suppress=True , linewidth=200 ) import types, torchfrom torch.nn import functional as Ffrom tokenizers import Tokenizertokenizer = Tokenizer.from_file("20B_tokenizer.json" ) args = types.SimpleNamespace() args.MODEL_NAME = '/fsx/BlinkDL/HF-MODEL/rwkv-4-pile-430m/RWKV-4-Pile-430M-20220808-8066' args.n_layer = 24 args.n_embd = 1024 context = "\nIn a shocking finding, scientist discovered a herd of dragons living in a remote, previously unexplored valley, in Tibet. Even more surprising to the researchers was the fact that the dragons spoke perfect Chinese." NUM_TRIALS = 3 LENGTH_PER_TRIAL = 100 TEMPERATURE = 1.0 TOP_P = 0.85
RNN模型类 这部分实现了在已知预训练权重(代码中通过 self.w 读取并存储)的情况下,使用RNN模式进行前向过程的模型代码。
为了统一管理,在代码实现上,RWKV传递的了 state 这么一个二维数组参数。每个时间步 i,它都存储了5个向量:
state[5*i+0] 存储上一时间步的 Channel mixing 的输入变量x ′ x' x ′ state[5*i+1] 存储上一时间步的 Time mixing 的输入变量x x x state[5*i+2] 存储了 aa,即上一时间步的 a,是 RWKV-4 的 RNN 版本的中间变量,下同.state[5*i+2] 存储了 bb,即上一时间步的 b.state[5*i+2] 存储了 pp,即上一时间步的 p.state 在 Time mixing 和 Channel mixing 操作结束后的值都会更新,等待下一时间步参与计算。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 class RWKV_RNN (torch.jit.ScriptModule): def __init__ (self, args ): super ().__init__() self.args = args self.eval () w = torch.load(args.MODEL_NAME + '.pth' , map_location='cpu' ) for k in w.keys(): if '.time_' in k: w[k] = w[k].squeeze() if '.time_decay' in k: w[k] = -torch.exp(w[k].float ()) else : w[k] = w[k].float () self.w = types.SimpleNamespace() self.w.blocks = {} for k in w.keys(): parts = k.split('.' ) last = parts.pop() here = self.w for p in parts: if p.isdigit(): p = int (p) if p not in here: here[p] = types.SimpleNamespace() here = here[p] else : if not hasattr (here, p): setattr (here, p, types.SimpleNamespace()) here = getattr (here, p) setattr (here, last, w[k]) def layer_norm (self, x, w ): return F.layer_norm(x, (self.args.n_embd,), weight=w.weight, bias=w.bias) @torch.jit.script_method def channel_mixing (self, x, state, i:int , time_mix_k, time_mix_r, kw, vw, rw ): xk = x * time_mix_k + state[5 *i+0 ] * (1 - time_mix_k) xr = x * time_mix_r + state[5 *i+0 ] * (1 - time_mix_r) state[5 *i+0 ] = x r = torch.sigmoid(rw @ xr) k = torch.square(torch.relu(kw @ xk)) return r * (vw @ k) @torch.jit.script_method def time_mixing (self, x, state, i:int , time_mix_k, time_mix_v, time_mix_r, time_first, time_decay, kw, vw, rw, ow ): xk = x * time_mix_k + state[5 *i+1 ] * (1 - time_mix_k) xv = x * time_mix_v + state[5 *i+1 ] * (1 - time_mix_v) xr = x * time_mix_r + state[5 *i+1 ] * (1 - time_mix_r) state[5 *i+1 ] = x r = torch.sigmoid(rw @ xr) k = kw @ xk v = vw @ xv aa = state[5 *i+2 ] bb = state[5 *i+3 ] pp = state[5 *i+4 ] ww = time_first + k qq = torch.maximum(pp, ww) e1 = torch.exp(pp - qq) e2 = torch.exp(ww - qq) a = e1 * aa + e2 * v b = e1 * bb + e2 wkv = a / b ww = pp + time_decay qq = torch.maximum(ww, k) e1 = torch.exp(ww - qq) e2 = torch.exp(k - qq) state[5 *i+2 ] = e1 * aa + e2 * v state[5 *i+3 ] = e1 * bb + e2 state[5 *i+4 ] = qq return ow @ (r * wkv) def forward (self, token, state ): with torch.no_grad(): if state == None : state = torch.zeros(self.args.n_layer * 5 , self.args.n_embd) for i in range (self.args.n_layer): state[5 *i+4 ] = -1e30 x = self.w.emb.weight[token] x = self.layer_norm(x, self.w.blocks[0 ].ln0) for i in range (self.args.n_layer): att = self.w.blocks[i].att x = x + self.time_mixing(self.layer_norm(x, self.w.blocks[i].ln1), state, i, att.time_mix_k, att.time_mix_v, att.time_mix_r, att.time_first, att.time_decay, att.key.weight, att.value.weight, att.receptance.weight, att.output.weight) ffn = self.w.blocks[i].ffn x = x + self.channel_mixing(self.layer_norm(x, self.w.blocks[i].ln2), state, i, ffn.time_mix_k, ffn.time_mix_r, ffn.key.weight, ffn.value.weight, ffn.receptance.weight) x = self.w.head.weight @ self.layer_norm(x, self.w.ln_out) return x.float (), state
Logits输出 该步骤将模型的输出 x.float()(即 out/logit)进行 softmax 处理,并根据参数 temperature 和 top_p 随机选取出一个样本,并返回所选的 token 索引。
说人话就是,这一步正在根据已喂到的文本随机挑出下一个单词的索引 ,当然这个单词要真正打印出来,还需要使用 tokenizer 进行解码。
1 2 3 4 5 6 7 8 9 10 11 def sample_logits (out, temperature=1.0 , top_p=0.8 ): probs = F.softmax(out, dim=-1 ).numpy() sorted_probs = np.sort(probs)[::-1 ] cumulative_probs = np.cumsum(sorted_probs) cutoff = float (sorted_probs[np.argmax(cumulative_probs > top_p)]) probs[probs < cutoff] = 0 if temperature != 1.0 : probs = probs.pow (1.0 / temperature) probs = probs / np.sum (probs) out = np.random.choice(a=len (probs), p=probs) return out
NOTE:代码中的 token 这个变量一直是索引的存在,从 RWKV_RNN.forward() 中也能看出,是通过调用词嵌入 self.w.emb.weight[token] 才取出的向量表示x 的。对应地,sample_logits 的输出也是随机预测到的单词的索引。
LM推理 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 print (f'\nUsing CPU. Loading {args.MODEL_NAME} ...' )model = RWKV_RNN(args) print (f'\nPreprocessing context (slow version. see v2/rwkv/model.py for fast version)' )init_state = None for token in tokenizer.encode(context).ids: init_out, init_state = model.forward(token, init_state) for TRIAL in range (NUM_TRIALS): print (f'\n\n--[ Trial {TRIAL} ]-----------------' , context, end="" ) all_tokens = [] out_last = 0 out, state = init_out.clone(), init_state.clone() for i in range (LENGTH_PER_TRIAL): token = sample_logits(out, TEMPERATURE, TOP_P) all_tokens += [token] tmp = tokenizer.decode(all_tokens[out_last:]) if '\ufffd' not in tmp: print (tmp, end="" , flush=True ) out_last = i + 1 out, state = model.forward(token, state) print ('\n' )
参考 免注意力Transformer (AFT):使用逐元素乘积而不是点积 - 鸽鸽的书房 - 博客园 颠覆Transformer?新语言模型算法RWKV解读 【手撕LLM-RWKV】重塑RNN 效率完爆Transformer - 知乎 RWKV架构及历史 - RWKV文档