DS简介与线性表|数据结构Ⅰ
概述
数据结构(data structure) 是相互之间存在一种或多种特定关系的数据元素的集合,即带“结构”的数据元素的集合。因此在存储数据时,不仅要存储数据元素的值,还需指示数据元素之间的关系。
1 | Data_Structure(D, R); |
其中 是数据元素的集合, 是该集合中所有元素之间的关系的有限集合。
数据结构具体指同一类数据元素中各元素之间的相互关系,包括三个组成成分,数据的逻辑结构、存储结构和数据运算结构。
数据的逻辑结构是从实际问题出发,只采用抽象表示方法,独立于存储结构的。而数据的存储结构是逻辑结构在计算机中的映射,不能独立于逻辑结构而存在。
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。
把现实中大量而复杂的问题以特定的数据类型和特定的存储结构保存到主存储器(内存)中,以及在此基础上为实现某个功能(比如查找某个元素,删除某个元素,对所有元素进行排序)而执行的相应操作, 这个相应的操作也叫算法
关于算法的复杂度计算以及各类经典算法详见:算法分析与设计 & 本站算法综述
预备知识
指针
……从略……
结构体
如果与C++,Java,Python中的“类”进行类比的话,C语言中的结构体就相当于“没有方法的类”。
下面是一个简单的结构体示例:
1 |
|
从上面的示例,可以简单了解到定义结构体的方法,和如何使用结构体成员。更多详细的内容这里不予给出,请自行移步至 C语言 的相关书籍、资料和视频。
动态分配内存
动态内存分配(Dynamic Memory Allocation)就是指在程序执行的过程中动态地分配或者回收存储空间的分配内存的方法。
与之相比,int a[100];就相当于从程序运行起,操作系统就“死死”的为程序开辟了400个字节的空间。(400 = 100 * 4 数据个数乘以 int 型数据所占的空间)
“动态”一词表明可以在程序中灵活的开辟指定数量指定类型的空间,而且还可以动态释放。
Tip:任何类型的指针变量都是占用4个字节(32位系统)。
建立动态内存
1 |
|
确定想要分配的动态内存的数据类型,定义相应类型的指针变量。如
int确定想要分配的内存大小,如100个
int型数据的内存,可通过sizeof(此处传入数据类型)*数量的方法得到字节大小使用
malloc()函数实现分配malloc函数是C标准库中的函数,可通过引入头文件
stdlib.h使用其内部的函数声明如下:
1
void *malloc(size_t size)
参数:内存大小(字节为单位)
返回值:void的不确定指针,请求失败则返回NULL
由于返回值是不定指针,因此我们分配时需要强制类型转换
将得到的指针赋值给之前定义好了的指针变量
之后这个指针即可当作普通数据来使用
内存的释放:使用函数
free(指针变量名)即可
拓展知识|加深理解
指针即是地址,指针变量即是记录有或者说指向有地址的一个变量,通常只指向“首地址”。
如:
上述示例中的“指针数组pArr”,pArr这个变量其本身指向的就是该数组内的第一个元素(在示例中是)45的 这个int型数据 它 所占的 第一个字节 的地址(int型数据占4个字节)。
而定义该变量时/分配内存时,有int *的存在,表明(相当于告诉指针)这是个int型数据的首地址,“所以,以后的字节你都4个4个的看成一个数据来处理,直到给定范围结束后停止”。
相当于指针始终只是指向一系列字节的首个地址,然后通过其类型和长度能得以取出各个数据。
线性表
线性表是由 个同类型的数据元素组成的有限序列,标记为:
其中, 为表长,当 时线性表为空表。
- 是唯一的第一元素,称表头元素;对应的 为表尾元素。
- 除表头外,每个元素有且仅有一个直接前驱;除表尾外,每个元素有且仅有一个直接后继。
- 线性表中的每个元素有唯一的序号(逻辑序号),同一个线性表中可以有多个相同的元素,但他们的序号是不同的。
线性表是一种逻辑结构,表示元素之间一对一的相邻关系;
顺序表和链表是指存储结构,二者属于不同层面的概念,请勿混淆。
线性表的基本操作
InitList(&L):初始化。其作用是建立一个空表(即建立线性表的构架,但不含任何数据元素)。DestroyList(&L):销毁。其作用是释放线性表 的内存空间。ListLength(L):返回线性表 的长度。GetElem(L,i):按位查找。返回线性表 的第 个数据元素。LocateElem(L,x):按值查找。若 中存在一个或多个值与 相等的元素,则其作用是返回第一个值为 的元素的逻辑序号。ListInsert(&L,i,x):在 的第 个位置上增加一个以 为值的新元素。ListDelete(L,i):删除线性表的第 个元素。DispList(L):输出操作。其作用是按前后次序输出 的所有元素值。Empty(L):判空。判断线性表是否为空,为空返回true。
连续存储| 顺序表
线性表的顺序存储又称顺序表。它是用一组地址连续的存储单元依次存储线性表中的元素,从而使得逻辑上相邻的元素在物理位置上也相邻。第一个元素存储在线性表的起始位置。
由于元素大小和存储的地址顺序已知所以顺序表可以实现任一数据元素的随机存取。即直接通过首地址和元素序号实现 时间的存取。
但是相反,对于插入和删除就需要移动大量元素。
顺序表可利用高级程序设计语言中的数组描述。
根据 C 语言的不同编写方法,一维数组也有静态分配和动态分配之分。
前者的数据大小和空间因为实现固定,所以一旦空间占满再想加入元素便会产生溢出。
后者可实现动态申请。注意,当前 个空间满时,若还需要 个空间,则系统需要找到 个连续空间才能申请成功。
以下将展现以数组方式构建的一个简单的`int`型顺序表。要求实现:
- 实现动态分配
- 实现长度记录
- 实现有效长度记录
- 实现自动扩充长度
- 实现数组的输出
- 实现数组元素的增删改
建立基础框架
创建顺序表结构体
1 |
|
初始化与基础判断
此处声明的函数名和前面介绍线性表时有所出入,注意甄别;
此处的实现利用指针,而非 C++ 中的引用实现;
此处默认 Arr.length 即数组长度是以1为起点。
数组初始化
1 | void Init_arr(Arr *List,int InitSize){ |
判断是否为空/已满
1 | bool IsEmpty(Arr *List){ |
插入与删除元素
追加数据元素(加至最后一行)
1 | bool append(Arr *List,int value){ |
插入/删除元素(数据自动收缩)
注:此处的插入与删除 所给的参数是pos,即是位置,是从1开始计数的;而此处的插入则是在所选择位置的左边插入,如:
[1,1,1,1,1,1]中,在pos = 3处插入2,得到的是[1,1,2,1,1,1,1]
1 | bool insert(Arr *List,int pos,Datatype value){ |
最好情况下,插入直接在表尾进行,时间复杂度
最坏情况下,在表头处插入,时间复杂度
平均情况下,插入点 pos 可选的位置有 个,等概率情况下选择第 个位置的概率 ,而此后需要移动 之后的 个元素的位置。则有:
即平均时间复杂度为.
取值与翻转元素
对顺序表进行翻转
1 | void Inversion(Arr *List){ |
时间复杂度 .
将数组特定位置元素取出(按值查找)
1 | ElemType getPos(Arr *List, ElemType x){ |
平均情况下,元素 可能的位置有 个,等概率情况下出现在第 位的概率 ,则有:
即平均时间复杂度为.
删除所有特定元素
对长度为 的顺序表 设计算法实现删除线性表中所有值为 的数据元素。
该问题有两种解决策略。
方法一:用 来记录线性表中不含 的元素个数(即需要保留的元素个数),在扫描的过程中不断更新 的值,因此需要保留的元素的下标与 是完全同步的。
例如顺序表 中,扫描到 后, 的值不再变化,当继续扫描到 之后,才把 放到 的位置上。也就是说 正好与当前元素是第几个不为 的元素对应。
方法二:用 来记录线性表中等于 的元素个数,在边扫描边统计 的时候,将不为 的元素左移 个位置。
例如顺序表 中,扫描到 3 时,统计出此前表中有1个值是 的元素,即 ,所以我们需要将 3 左移 1 位;而扫描到 4 时左移2位。
两种方法的实现如下:
1 | void del_all_methrod1(Arr *List, ElemType x){ |
时间复杂度为.
对长度为 的顺序表 设计算法实现删除线性表中 的数据元素。
解决该问题的算法思想与上面的方法二类似。我们只需要利用 来记录处于区间 的元素个数,然后不属于该区间的元素左移 位即可。
所以,我们将上面编写的 del_all_methrod2() 中第三行的判断语句改为:List.pData[i] >= s && List.pData[i] <= t 即可。
整体分块换序与移位
对长度为 的顺序表
设计算法实现将其前 个元素 与后 个元素进行位置交换。
即,使得新的顺序表变为
将问题抽象为把数组 转变为 .
想象这样的操作:如果我们对 进行翻转得到 ,再对 翻转得到
最后再整体翻转:.
那么问题将得以解决!
而我们上面编写的翻转代码(Inversion(Arr*))只能实现对整个顺序表的翻转,因此我们还需再次对其进行改造,变为更加通用的函数,实现给定边界的局部的翻转:
1 | void Reverse(Arr *List, int left, int right){ |
于是,实现 就相当于进行三次翻转:
1 | void ExchangeBlock(Arr *List, int m, int n){ |
对长度为 的顺序表
设计算法实现将表中的元素循环左移 个单位 ()
即,使得新的顺序表变为【2010年统考】
分析之后可得,这与上面的问题无异,相当于把顺序表中的前 个元素与后 个元素进行位置互换而已。
1 | void Converse(Arr *List, int n, int p){ // n 是数组个数 |
三次翻转的时间复杂度分别是 ,总体时间复杂度还是.
两组顺序表的中位数
对长度为 的 升序序列 ,其中位数就是 .
要求设计算法实现给出 组合在一起后的中位数。【2011年统考】
如 则其中位数是11. 要想高效地实现中位数的输出,我们应该充分利用所给序列是有序序列这一特性。
试想,如果我们分别知道 的中位数,那么二者结合起来的中位数一定在中位数小的那一组的右边,中位数大的那一组的左边。也就是说,我们并不需要先把二者完全合并然后再取中间值。
有了这个思路之后,我们可以利用分治策略,更进一步地进行推广。
假设已知 的中位数分别是 ,且 。这说明应该取 的左半部分(记为 ), 的右半部分(记为 )。于是,我们就又可以考察 的中位数 和 的中位数 ,如此迭代下去。直到被我们两两子序列只含有一个元素为止。
综上所述,该策略的时间复杂度仅为 ,空间复杂度.
离散存储| 链表
链表是一种物理存储单元上非连续、非顺序的[存储结构],元素的逻辑顺序是通过链表中的指针链接次序实现的。
链表由一系列结点(Node)组成,结点可以在运行时动态生成
注:链表中每一个元素称为结点。此外也有节点这样的翻译 ~因此以下内容可能会出现有节点和结点混用的情况,但也无伤大雅~
由于链表是一系列Node通过指针串接起来形成的,因此每个Node至少有两个域,一个域用于数据元素的存储,另一个或两个域是指向其他单元的指针。这里将两个域命名为:数据域、指针域
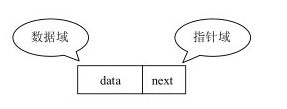
容易得出这样的结论:链表不能实现随机存取,查找特定结点时需要从表头开始遍历,依次查找。
链表的分类
单链表:每个链表的指针域只能指向后面的节点
双链表:每一个节点有两个指针域,分别指向前一个节点和后一个节点
循环链表:能通过任何一个节点找到其他所有的结点,最后一个节点的指针指回第一个节点
非循环链表:指向中不出现循环的链表
链表的组成元素
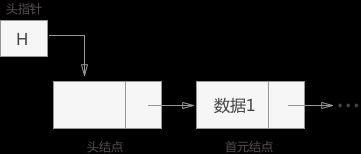
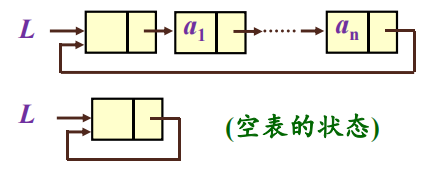
头结点
头节点的数据类型和首结点的数据类型相同。在首结点的前一项,一般不用于存放有效数据
,也可以用于记录表长等信息。而设计链表时加头结点的目主要是为了方便对链表进行一些统一划归,避免对首个元素的复杂操作。头结点的指针域指向线性表的第一个元素结点。头指针(head):指向链表的指针变量,是一个链表的标识,例如头指针为
NULL时表示该链表为空表。无论一个链表的设计带不带头结点,头指针都始终指向链表的第一个结点。首结点:第一个有效节点,又译:首元结点
尾结点:最后一个有效元素结点
尾指针(tail):指向尾节点的指针变量
单链表的基本操作
单向链表中,除了首尾数据元素外,其它数据元素都是首尾相接的。
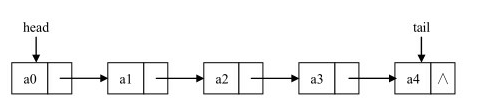
我们可对单向链表的结点类型做如下描述:
1 |
|
头插法建立单链表
头插法建立单链表的思想是,从一个空表开始,生成新结点,并将读取到的数据存放到新结点的数据域中,然后总是将新结点插入到当前链表的表头,也就是头结点之后,如图所示。

下面给出仅给出元素 的情况下的链表建立,目的在了解头插法的链接逻辑,可拓展为建立之初就不断插入多个元素。
1 | /* |
可见,采用头插法建立单链表时,读入数据的顺序与生成链表中元素的顺序是相反的。为此,还有一种建立单链表的方法,即尾插法。
尾插法建立单链表
尾插法将新结点插入到当前链表的表尾,并增加一个表尾指针 ,使其始终指向当前链表的尾结点,如图所示。

1 | /* |
由于引入了尾指针,所以时间复杂度也有所降低。综上,尾插法与头插法的均为 的时间复杂度。(因为实际上在建立时会不断插入多个元素,假设规模是)
查找结点| 按序号与值
链表只能通过头指针,不断顺着 pNext 往下搜索至少 次才能找到所需结点:
1 | LNode *GetElem(LinkList L, int k){ |
按值查找同理,需要依次进行比较:
1 | LNode *LocateElem(LinkList L, ElemType x){ |
遍历链表的方法同样可以用来求链表长度,下面就不再赘述了。
值得注意的是,头结点不计入长度计算中!
插入结点| 前后插操作
插入结点操作将值为 的新结点插入到单链表的第 个位置上.
- 先检查插入位置的合法性
- 找到待插入位置的前驱结点,即第 个结点,然后在其后插入新结点。
算法首先调用按序号查找算法 GetElem(L,i−1),查找第 个结点 *p,然后再修改指针指向,实现插入,具体如下图所示。

1 | p = GetElem(L, i-1); //查找插入位置的前驱结点 |
算法中的后两个语句顺序不能颠倒,否则将失去指向插入位置的后继结点的指针。
链表的插入通常使用的是后插操作,而对于前插操作,也就是说在指定结点的前面插入结点,我们同样可以转化为对链表的后插操作,无外乎将指定序号-1。
当然,如果并不是对指定序号的结点进行前插,而是只知道目标元素值 的结点 *p却不知道序号,那处理起来就棘手得多。
我们需要先遍历一次链表得到它的前驱结点*q,这样才能将新结点 *s 放入 *q 的后面,即 *p 的前面。
可见这样的处理方法,其时间复杂度将达到.
下面提供一种别的思路:
仍然做后插处理,但对指定结点*p 与我们刚刚插入的这一项 *s 进行元素值的交换。
这样同样实现了前插,但复杂度降到了。
1 | s->next = p->next; |
删除结点| 释放空间
与插入结点十分相似,将单链表的第 个结点删除,同样要先检查删除位置的合法性,然后查找表中第 个结点,即被删除结点的前驱结点,再通过修改其指针域内容的方式将其从整个链表中隔离开,最后对其空间释放,以实现真正的删除。
实现删除的代码如下:
1 | p = GetElem(L, i-1); //查找被删除结点的前驱结点 |
与上面讨论前插操作类似,如果我们不知道被删除结点所在的序号,但事先得到了其结点本身,如 *q ,那么如果再遍历一遍找到它的前驱就又得消耗 的时间了。
这时,我们的“交换元素大法”再次奏效了。
我们在已知 *q 的情况下,可以获得它的后继结点 *p。我们直接对二者元素进行交换,然后把 *q 的后继指针指向 *p 的后继。这样,含有我们不需要的旧元素的 *p 就被剥离出链表,对其 free 即可。时间复杂度降到了.
1 | p = q->next; //得到q的后继结点 |
双链表与循环链表
单链表结点中只有一个指向其后继结点的指针,使得单链表只能从头到尾依次顺序地进行遍历。
在前面的分析中我们也发现了,无论是前插操作还是结点删除,想要找到前驱结点就需要 ,想要找到后继只需要 。导致复杂度差异如此之大的原因就是单链表有着指向后继的指针。因此,如果我们对前驱结点也建立相应的指针指向它,那么就可以克服如此困难了。
于是,双链表应运而生,我们在 next 指针的基础上,再添加 prior 指针。
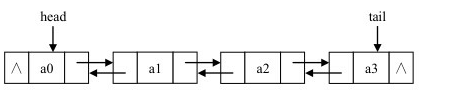
同时,结构体也应该调整:
1 | typedef struct DNode{ //Double |
双链表的插入删除
链表的创建,自然双链表也有单链表类似;结点的查找也是一脉相承;结点的插入与删除由于指针的引入变为了。
但是插入和删除操作由于设计到指针的各种调整,其指针的变换顺序也有梳理的必要。所以我们主要探讨下双链表下进行插入删除分别需要进行的指针域调整。
- 考虑插入
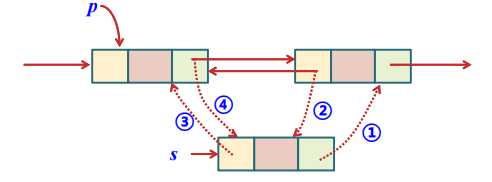
如图所示,当我们指定在结点 之后插入新结点 后,我们应当保证:
1 | s->next = p->next; //首先, 将s的后继指针指向p原本的后继 |
上述代码与图中的 是一一对应的。其中,2、3的顺序可做调换,但是(1)→(2),(2,3)→(4) 的顺序则不能调换。
试想,如果我们先将 的后继指针指向,那么我们将无法锁定 原本的后继,从而 就无法链入链表了。
换句话说,欲插入结点时,结点 和目标位置 是给定的,但是 是可变的,所以应当优先保证在不更换 的情况下把其他指针调整好。
- 考虑删除
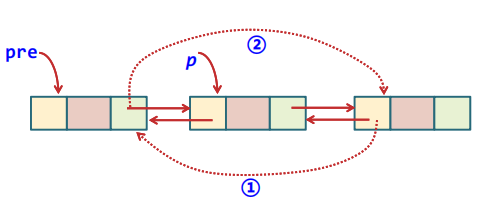
欲删除结点时,虽然只有目标结点 是给定的,但先(1)后(2)还是先(2)后(1)都不会造成影响。
从而有:
1 | p->next->prior = p->prior; //p的后继结点的前驱指针指向p的前驱结点pre |
循环单链表
循环单链表是单链表的变形,链表尾结点的 next 指针不是 NULL,而是指向了单链表头结点,从而整个链表形成一个环,如下图所示。
因此,我们有:
- 循环链表的判空条件:
L->next == L; - 只要知道表中某一结点的地址,就可遍历到所有其他结点的地址。
- 在搜索过程中,没有一个结点的
next域为空。 - 遍历条件:
for ( p = L->next; p != L; p = p->next ) - 循环单链表的所有操作的实现类似于单链表,差别在于涉及到
链尾时需单独处理。
有时对单链表常做的操作是在表头和表尾进行的,对应下来如果采用循环单链表,我们则一般只需设置表尾指针。这是因为如果设置表尾,则表头就是 ,而如果设置表头,则需要 的查找表尾时间。
循环双链表
在循环双链表中,头结点的 prior 指针指向表尾结点
当循环双链表为空表时,其头结点的 prior和 next 指针域都等于 L
链表的更多操作/算法
删除所有符合条件的结点
和顺序表类似,在链表中,也可以利用之前我们讨论过的两种方法实现批量删除结点。同样以“删除数据值为 的结点”为例。
当时我们的方法一是用 记录不为 的结点个数,同时 正好作为下标。
这里也一样,我们用指针 p 遍历链表,用指针 r 表示遍历过程中应当保留的链表末位结点。若 p 的数据值为 ,则 r 停留在此处,p 继续前进。若 p 的数据域不是要删除的 ,利用尾插法的思想,找到 p->data ≠ x 时,将其插入尾结点之后,即让 r->next = p,然后 r, p 同步向下移。
1 | void del_all_methrod1(LinkList L, ElemType x){ |
当时我们的方法二是用 记录数据值 的结点个数,其后的结点全都左移 位。
这里也一样,我们用指针 p 遍历链表,用指针 pre 表示 p 的前驱结点。若 p 的数据域正好是要删除的 ,则用 q 将其脱离链表,让 p 去下一个结点,并删除释放 q。否则,pre, p 同步前进。
1 | void del_all_methrod2(LinkList L, ElemType x){ |
单链表的原地逆置
原地逆置即在空间复杂度为 的情况下,对链表 实现元素顺序的逆序重排列。
联想到在介绍链表的建立时,我们采用的头插法会导致链接顺序与输入顺序相反。根据头插法的这样的特性,我们就得到了原地逆置的第一个方法。
方法一:将头结点摘下,依次从第一个结点开始,利用头插法重新组装链表,即可实现逆置。
1 | LinkList Reverse_1(LinkList L){ |
方法二:直接在遍历过程中,修改相邻结点的指针指向,一趟遍历即可把所有的指针反向,从而实现逆置。
为了不出现链接的丢失,至少需要三个指针依次指向链表中相邻的三个结点,我们用 pre, p, r 作为这样的三个指针。在调整指针指向时,把 p 作为主心骨,每次都对 p 处理,pre 指向原本链表的前驱,r 指向原本链表的后继,以免丢失。
1 | LinkList Reverse_2(LinkList L){ |
时间复杂度 ,空间复杂度。
利用插入排序实现结点重排
利用插入排序算法的思想,先建立只有一个结点的有序单链表 ,用 p 实现依次扫描 中剩下的结点,通过比较 p 与 有序单链表 的结点 pre 数据值的大小(pre 需要实现遍历 ),然后选择合适的位置将其插入 中。
该过程为了防止断链,还需要引入 r 指针指向 p 的后继。
1 | void SortList(LinkList L){ |
该算法受限于链表本身的性质,再加上采用的是插入排序,所以时间复杂度是 。
如果我们可以用数组作为辅助空间,那么将数据复制到数组一趟需要 ,在数组中利用快排进行排序需要 ,然后再从数组中复制回来一趟需要 。综合起来,只需要 ,这是比 快的。是一种利用空间换时间的思想。
两个链表的公共结点
两个单链表有公共结点,即是两个链表从某一个结点开始,它们的指针域指向了同一个结点。
不难得出,从两个链表的公共点往后,它们的所有结点都是完全重合的了。也就是说,从第一个公共结点开始,两个链表的拓扑结构应该是 形,而不会出现 形。
显然,利用暴力算法可以解决这个问题,嵌套两个循环来遍历链表,这样时间复杂度将达到 ,其中 分别是两个链表的长度。
但事实上,根据我们上述分析,该问题是存在线性时间复杂度是算法的。如果两个链表有公共结点,那么它们的最后一个结点一定相同,反之它们一定不存在公共结点。
按照从后往前推的思想,公共结点之后的两个链表的长度是相同的。考虑极端情况,较短的那个链表如果一开始就与较短的链表重合,那么较长链表的前 个结点是没有必要的。(假设从 个结点开始,可以和较短链表同步遍历)
综上所述,对于长度分别为 的两个链表,我们只需先将 遍历到 个结点处,然后两个链表同步遍历,知道发现公共结点或遍历到尾结点仍然不相交为止。时间复杂度为
1 | LinkList Common_1st_Node(LinkList L1, LinkList L2){ |
链表的交集归并
将两个元素递增排列的链表 视为集合。将两者的交集作为新链表给出。要求新链表存放于 中。
采用归并思想,设置两个工作指针 p, q 对两个链表进行遍历。通过指针 r 在 的基础框架上做插入操作,实现当扫描到数据值相同的结点时,把该结点插入当前以 r 为主的新链表中,而不相等的结点进行释放。
1 | LinkList Union(LinkList L1, LinkList L2){ |
频度最大优先双链表
对于含有 [prior, next, freq] 的非循环双向链表, 设计算法实现每对 调用一次 locate(x) 查找数据域为 的结点,都将其频度自增,并且把链表按照频度递减排列,使得频繁被访问的结点在最前面。频度相同的结点,最近被访问的排在前。
设计函数 FreqFirst_Locate(DLinkList, ElemType); 实现该功能。
具体思想是,利用 p 遍历,找到 p->data == x 的结点并摘下。然后依次与排列在它之前的结点(用 q 遍历)进行比较,直到找到第一个数值比它大的结点 q,然后将 p 插入其后。
1 | DLinkList FreqFirst_Locate(DLinkList L, ElemType x){ |
有环单链表的判定
单链表有环是指单链表最后一个结点的指针指向了链表中出现过的某个结点。要求设计算法实现判断某个给定的单链表是否有环,如果有返回环的入口结点。
不难想象单链表有环时的拓扑结构,我们可以类比于一个长条跑道接上一个环形跑道。
我们知道,当两个人在环形跑道上以不同的速度跑步时,除了起点以外,随着时间的推移,跑得快的人会在跑了 圈之后,与跑得慢的人第一次相遇。
这里我们采用的就是这样的思想。
我们利用两个指针 slow, fast 分别以步长 1 和步长 2 遍历链表。假设链表环长,开头的无环直链的长度为,fast 与 slow 相遇时,fast 在环中已经在遍历了 趟(正在跑第 圈),二者在环中相遇的位置距离入口点的长度为,则有:
解得:,即起点到相遇点的长度正好是环长的整数倍。
所以,如果设置一个新结点 q 从 slow 和 fast 的相遇点出发不断绕环,而另起一个新结点 p 同时从起点出发,与 slow 同步行动。那么当 p 与 q 相遇时, q 走过的路程是,p 走过的也是 。事实上,也就是 . 即此时 p 的位置就是入口点。
1 | LinkList FindLoopStart(LinkList L){ |
区别于直接开辟空间记忆各个结点然后逐步比较的算法,那样的时间复杂度达 之大。
注意到 slow 和 fast 第一次相遇时,slow 一定没有完整的走过一圈,所以我们给出的算法的时间复杂度为.
两种表的比较
存取方式
顺序表可以顺序存取,也可以随机存取,而链表只能顺序存取
逻辑结构和物理结构
顺序表中,逻辑上相邻的元素其对应的物理存储位置也相邻。而链表中,逻辑上相邻的元素其物理存储位置则不一定相邻,其对应的逻辑关系是通过指针域来表示。
查找、插入和删除操作
对于按值查找,顺序表无序时,两种存储方式的时间复杂度均为 ;
而当顺序表有序时,采用折半查找法的时间复杂度均为 。
对于按序号查找,顺序表支持随机访问,时间复杂度为 ,而链表的平均时间复杂度为。
顺序表的插入、删除操作平均需要移动半个表长的元素,而链表只需要修改相关结点的指针域即可。但由于链表的每个节点都有指针域,在存储空间密度上要比顺序表小。
空间分配
顺序存储在静态存储分配下,一旦存储空间装满则不能扩展,若再加入新的元素则就会发生内存溢出的情况,因此需要预先分配足够大的存储空间。但是如果预先分配过大,可能会导致顺序表空间的闲置,分配过小又会导致内存溢出。
而动态存储分配的存储空间虽然可以扩充,但需要移动大量元素完成操作,会导致算法运行效率降低,并且如果内存中没有合适的连续存储空间,则会导致动态分配失败。
链式存储的结点空间只在需要时进行申请分配,并且只要内存有空间就可以分配。
实际中应该如何选取
- 基于存储的考虑:
难以估计线性表的长度和存储规模时,首先考虑采用链式存储方式。 - 基于运算的考虑:
若经常需要进行按序号查找访问元素,首先考虑顺序存储;
若需要进行删除、插入操作较频繁,首先考虑链式存储。 - 基于环境的考虑:
顺序表较容易实现,一般通过数组类型定义即可实现;
链表的操作基于指针,较为复杂。




