Deep Neural Net | 多层感知机与神经网络入门
本站进阶深度学习汇总

感知机|PLA
感知机,具体来说是 Frank Rosenblatt 在1957年就职于Cornell航空实验室(Cornell Aeronautical Laboratory)时所提出来的,最古老的分类方法之一。原型被称为感知学习算法,即 Perceptron Learning Algorithm,简称PLA。
感知机算法的核心思想就是尝试找到一个超平面,把所有的二元类别隔开。
显然,使用感知机一个最大的前提,就是数据是线性可分的。这严重限制了感知机的使用场景。但是研究透了感知机模型,学习支持向量机的话会降低不少难度。同时再学习神经网络,深度学习,也是一个很好的起点。
算法原理
前面我们已经指出了 PLA 的核心思想,现在我们利用数学语言来更进一步地表征它。
若给定一个样本 ,其类别。则我们的目标就是找到一个超平面:
其向量形式为。我们希望落在这个超平面下方的点和上方的点属于不同的类别。即第 个样本 的类别可以表示为:
利用 函数,上式可以进一步化简:
学习算法
显然我们找超平面的目的等同于找到能够划分样本点的超平面的参数 和偏置。为此我们需要定义合适的目标函数以优化它,从而学习到参数。特别地,为了采用梯度下降法,我们更希望这个目标函数是可导/可微的。
我们知道每个样本点到超平面的距离 可以根据 本身具有的正负号性质化简为:
其中,分母表示超平面系数的 范数。注意该超平面是包含有 的,它可以看作是对扩展的样本属性值 的系数。
根据我们对PLA模型的定义不难得出,一个可以正确划分的 的符号总与该样本对应的类别 相同。所以二者相乘一定大于或零。
但是,如果存在划分错误的样例, 就一定有。
为了学习得到最优超平面,我们可以定义损失函数为所以划分错误的样例到超平面的距离:
其中, 表示第 个样本的预测类别; 为指示函数,当表达式为真时结果为1,为假时结果为0。
由于超平面的系数大小不影响对超平面的表示。如 可以写作,这使得 。因此我们同样能在保证系数 范数为1的情况下得到超平面。所以我们令,进一步化简损失函数。
多层感知机|MLP
当我们用下图所示的方式来可视化一个 PLA 时,我们可以得到一些有趣的思考方式:样本 的每一个维度/特征的输入 都可以视为一个个“神经元”,它们通过一个个“树突”(dendrites) 和“细胞核”(nucleus) 连接到“细胞体”(Cell body)中,最后通过“轴突”(axon)传递到下一个“神经元”。
| 单层感知机 | 真实的神经元 |
|---|---|
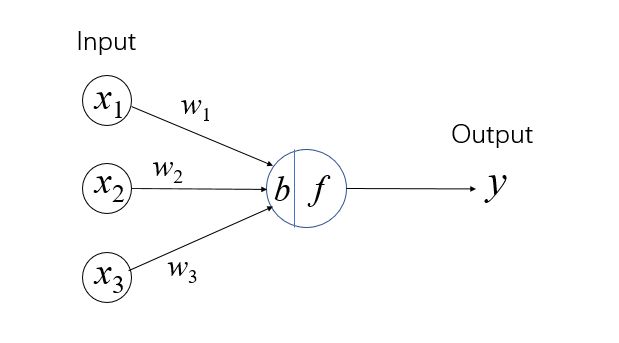 | 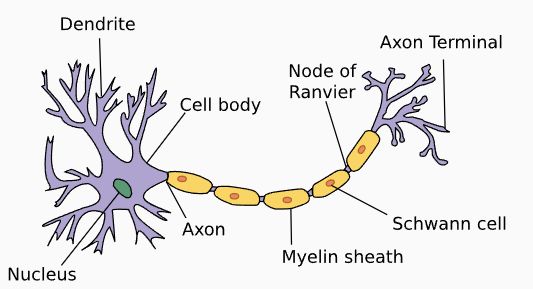 |
这就是从感知机到多层感知机最终被称为神经网络的起因。值得注意的是,神经网络虽然这样得名于“仿生学”的研究,但是其实际的作用机理乃至如今的蓬勃发展和现实中的人类神经几乎已经没有联系了。
一个简单的多层感知机 (Multi-Layer Perceptron,MLP) 可以用“神经网络”的可视化方法展示如下: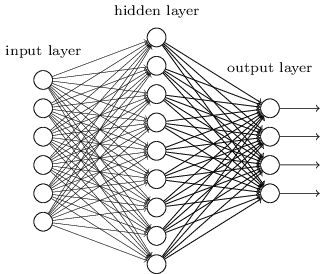
也许你已经注意到了,多层感知机 MLP 正是单层感知机 PLA 的级联和扩展。主要有以下几个特点:
- 隐藏层的加入。将第一层称为输入层,最后一层称为输出层,而中间的层称为隐藏层。每一层的输出不一定只有一个神经元,这些神经元我们也称为原始输入的隐藏变量;
- 激活函数的拓展。区别于PLA的 函数,MLP提供了更多的激活函数选择来应对不同输入数据类型以及输出的分类/回归结果。我们将在下一节展开。
由于历史渊源(提出于算力上不去那个年代),我们通常也把只有一个隐藏层,一共三层的多层感知机叫做:人工神经网络(Artificial Neural Network,ANN)
当隐藏层有 个神经元时,我们可以写出第 个隐藏层变量 的表达式(忽略激活函数):
其中, 分别表示第 个隐藏层的权重和偏置。上式还等价于:
对于一个输入样本 ,如果将其“嵌入”到维度(隐藏层变量个数)是 的“表示”中,那么所组成的 维隐变量 为:
由于计算机训练神经网络时通常是以一个批次为单位 batch_size,也就是说一次性可以并行计算 个维度(特征数)是 的样本。
那么所有 个样本的隐变量 可以用矩阵形式表示:
最后,我们以小批量的形式,给出一个人工神经网络的前向过程:
上标表示不同的层,不同层所用的权重和偏置也有所不同。
通用近似定理
灵活的神经网络层以及激活函数的选择赋予了多层感知机
代码实现
- Scikit-Learn 实现:sklearn 神经网络MLPclassifier参数详解-CSDN
- Pytorch 实现:【待更】
激活函数
机器学习中的数学——激活函数(五):ELU函数_elu激活函数-CSDN博客
昇腾大模型|结构组件-2——ReLU、GeLU、SwiGLU、GeGLU - 知乎
浅谈神经网络中激活函数的设计 - 科学空间|Scientific Spaces
Sigmoid
ReLU
目前神经网络最常用的激活函数:ReLU(Rectified Linear Unit)是Nair & Hintonw是在2010为限制玻尔兹曼机(restricted Boltzmann machines)提出的,并且首次成功地应用于神经网络(Glorot,2011)。除了产生稀疏代码,主要优势是ReLUs缓解了消失的梯度问题(Hochreiter, 1998;Hochreiteret al .)。值得注意的是,ReLUs是非负的,因此,它的平均激活值大于零。并且ReLU更容易学习优化。因为其分段线性性质,导致其前传,后传,求导都是分段线性。而传统的sigmoid函数,由于两端饱和,在传播过程中容易丢弃信息。
Tanh
正则化
权重衰减
early stop
Lasso回归/L2正则化
暂退法 Dropout
反向传播
https://blog.csdn.net/xholes/article/details/78461164
梯度消失/爆炸
参数初始化
NMT Tutorial 3扩展c. 神经网络的初始化 | Tingxun’s Blog (txshi-mt.com)
参数的对称性
Xavier初始化
Xavier 初始化是一种在训练深度学习模型时常用的权重初始化方法。它是 Xavier Glorot 和 Yoshua Bengio 在 2010 年提出的,原文为 Understanding the difficulty of training deep feedforward neural networks。
该初始化方法旨在保持激活函数的方差在前向传播和反向传播过程中大致相同,从而避免梯度消失或梯度爆炸的问题。
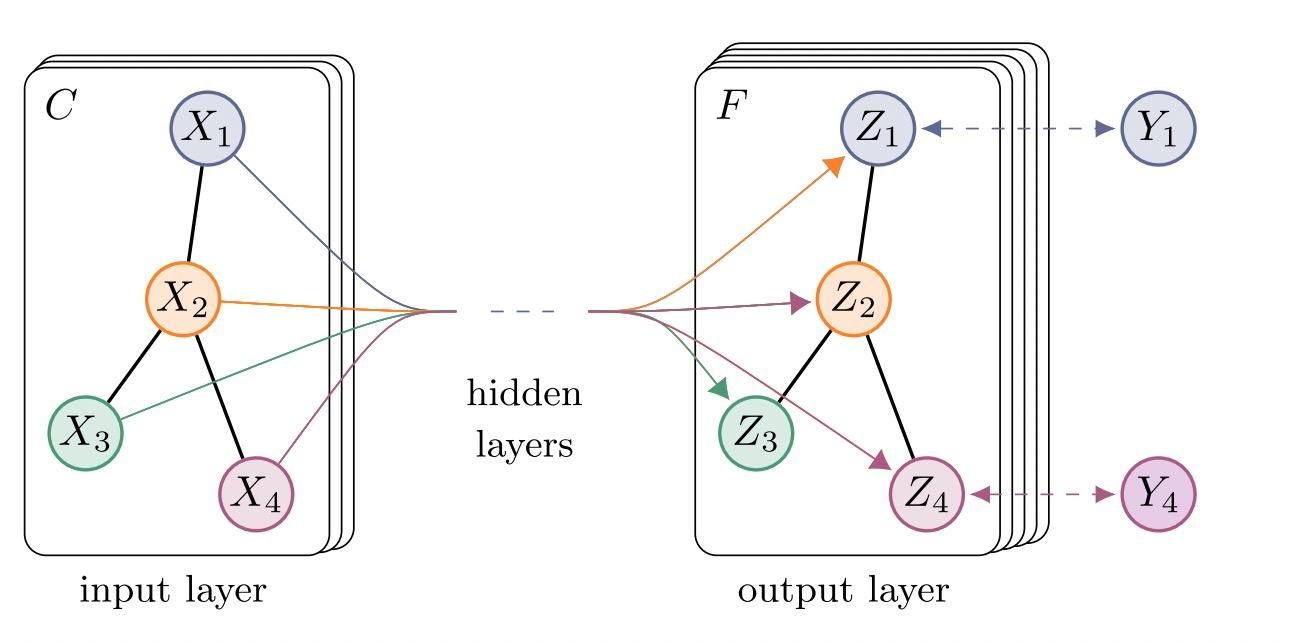
考虑一个简单的全连接层,该层接受 个输入并产生 个输出。每个输出 可以表示为:
如果输入 的方差为 ,则线性函数的方差将是 (忽略偏执和激活函数)。
Xavier 初始化试图使得每一层的输出的方差接近于其输入的方差。具体地,它取权重 的初始方差为:
这样无论如何,这一层的输出方差都接近于其输入方差。
当然考虑到偏置与激活函数,实际上所取的初始方差会更为复杂,需要一些推导,此处不做赘述了。
正如诸多参考资料指出的那样,xavier初始化只适用于关于0对称、呈线性的激活函数,比如 sigmoid、tanh、softsign 等。
而对于ReLU激活函数,可以采用 Kaiming 初始化、He 初始化,或 采用 Batch Normalization。
批量归一化
训练深层神经网络是⼗分困难的,特别是在较短的时间内使他们收敛更加棘⼿。而2015年提出的 批量归一化(Batch Normalization,BN)成为了⼀种流行且有效的技术,可持续加速深层⽹络的收敛速度。
批量归一化一般应⽤于单个可选层(也可以应用到所有层),其原理如下:
在每次训练迭代中,我们是总览一个批次 内的所有样本进行归一化,即通过减去其均值并除以其标准差,之后再调整适当的⽐例系数和⽐例偏移。
值得注意的是,这里的均值和标准差计算的是同一个特征不同样本数据之间的均值和标准差。

注意,如果我们尝试使⽤大小为 的小量应⽤批量归一化,我们将无法学到任何东西。这是因为在减去均值之后,每个隐藏单元将为0。
对全连接层
通常,我们将批量归一化层置于全连接层中的仿射变换和激活函数之间。如下式所示:
对卷积层
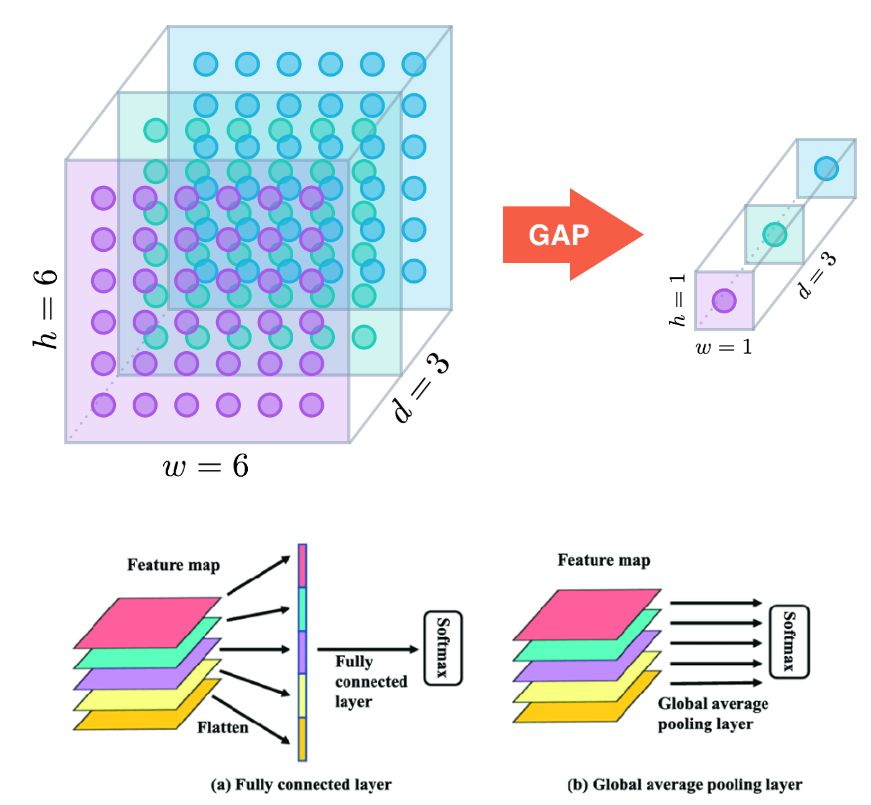
对于卷积层,我们可以在卷积层之后和⾮线性激活函数之前批量归一化。当卷积有多个输出通道时,我们需要对这些通道的“每个”输出都分别进行归一化,每个通道都有⾃⼰的拉伸(scale)和偏移(shift)参数(即)。
具体来说,我们对第 个特征图 中,处于 这个位置的像素点的值需要和该批次中所有落在这个位置的 个像素点进行统一的处理。
所以,一个批次就要对 个数据进行处理,归一化 次。其中 分别表示该特征图的高和宽。
对于预测过程
在训练过程中,我们⽆法得知使⽤整个数据集来估计平均值和⽅差,所以只能根据每个⼩批次的平均值和⽅差不断训练模型。
⽽在预测模式下,可以根据整个数据集精确计算批量规范化所需的平均值。
因为我们的模型是经过 BN 层训练得到参数的,所以预测时也应该对预测样本的数据进行归一化(否则结果就不对了)。而此时的均值和方差可以利用训练集的全体样本来计算而不再是批量样本。




