字符串与模式匹配|数据结构Ⅱ.2
串的定义与实现
串的定义
串(String)也称字符串,是由零个或多个字符组成的有限序列,记为:
其中 是串名,引号括起来的字符序列是串的值;
字符 可以是字母、数字、或其他字符;
串中字符的数目 称为串的长度,零个字符的串为空串,它的长度为零,用 表示。
由一个或多个空格(字符)组成的串称为空格串。空格串并不是空串!
串中任意连续的字符构成的子序列称为该串的子串,包含子串的串称为对应的主串。
子串在主串中的位置以子串中第一个字符在主串中的位置表示。
例如:s = "I am U" 中,s1 = "am" 就是 s 的一个子串。其中,'a' 在子串中的下标为 2,即 s[2] == 'a' 。该位置也是 s1 在 s 中的位置。
串的比较
当两个串长度相等并且对应位置的数据元素也相同时,则称两个字符串相等。
若不相等,则从第一个字符开始比较,谁的值大(通常比较 ASCII码)则所在的字符串大。
C 语言中
串的逻辑结构
串的逻辑结构与线性表极其相似。
区别在于,串的数据对象限定为字符集,并且在基本操作上,二者也有很大差别。
线性表的基本操作主要以单个元素作为操作对象,如:查找、删除或插入等。
串的基本操作通常以某个子串作为操作对象,涉及对子串的查找、删除或插入。
串的存储结构
定长顺序存储表示
类似于线性表的顺序存储结构,用一组地址连续的存储单元存储串值的字符序列。在串的定长顺序存储结构中,按照预定义的大小,为每个定义的串变量分配一个固定长度的存储区,则可用定长数组予以描述。
1 |
|
串的实际长度可以在预定义的长度范围内自定义,超过预定义长度的串值将被舍去,称之为“截断”。
串长有两种表示方法,一种是用额外的整型分量 length 来存放串的实际长度,正如上述描述一样。另一种是在串值后加一不计入串长的结束标记字符 \0 用于表示串的结束。
堆分配存储表示
在一些串的操作中,若串值序列长度超过上界,将会出现截断。为了克服这种弊端,我们采用动态分配的方式来表示字符序列。堆分配就是一种动态分配的存储表示方法。
堆分配存储表示依然使用一组地址连续的存储单元存放,但它的存储空间在程序执行过程中实现动态分配。
1 | typedef struct{ |
在 C 语言中,我们通过调用 malloc() 函数实现动态分配,这个过程是在堆中完成的。
块链存储表示
类似于线性表的链式存储,也可以利用链表来存储串值。
在具体实现时,每个结点既可以存放一个也可以存放多个字符,每一个结点称之为块,整个链表称之为块链结构。
C/C++ 中的串类
最小操作子集
待更
串的模式匹配
串的模式匹配是指子串的定位操作。即求子串(称模式串)在主串中的位置。
不同的模式匹配的算法实现有着不同的效率,下面我们将一一介绍各种算法。
Brute-Force算法
Brute-Force算法,简称 BF 算法,又称 朴素模式匹配算法。
顾名思义,BF 算法是一种暴力算法。
BF 算法的主要思想是:将主串的每一个字符与子串的开头进行匹配,匹配成功则比较子串与主串的下一位是否匹配;匹配失败则比较子串与主串的下一位,如此下去,直到所有字符都比较完毕。如下图所示:
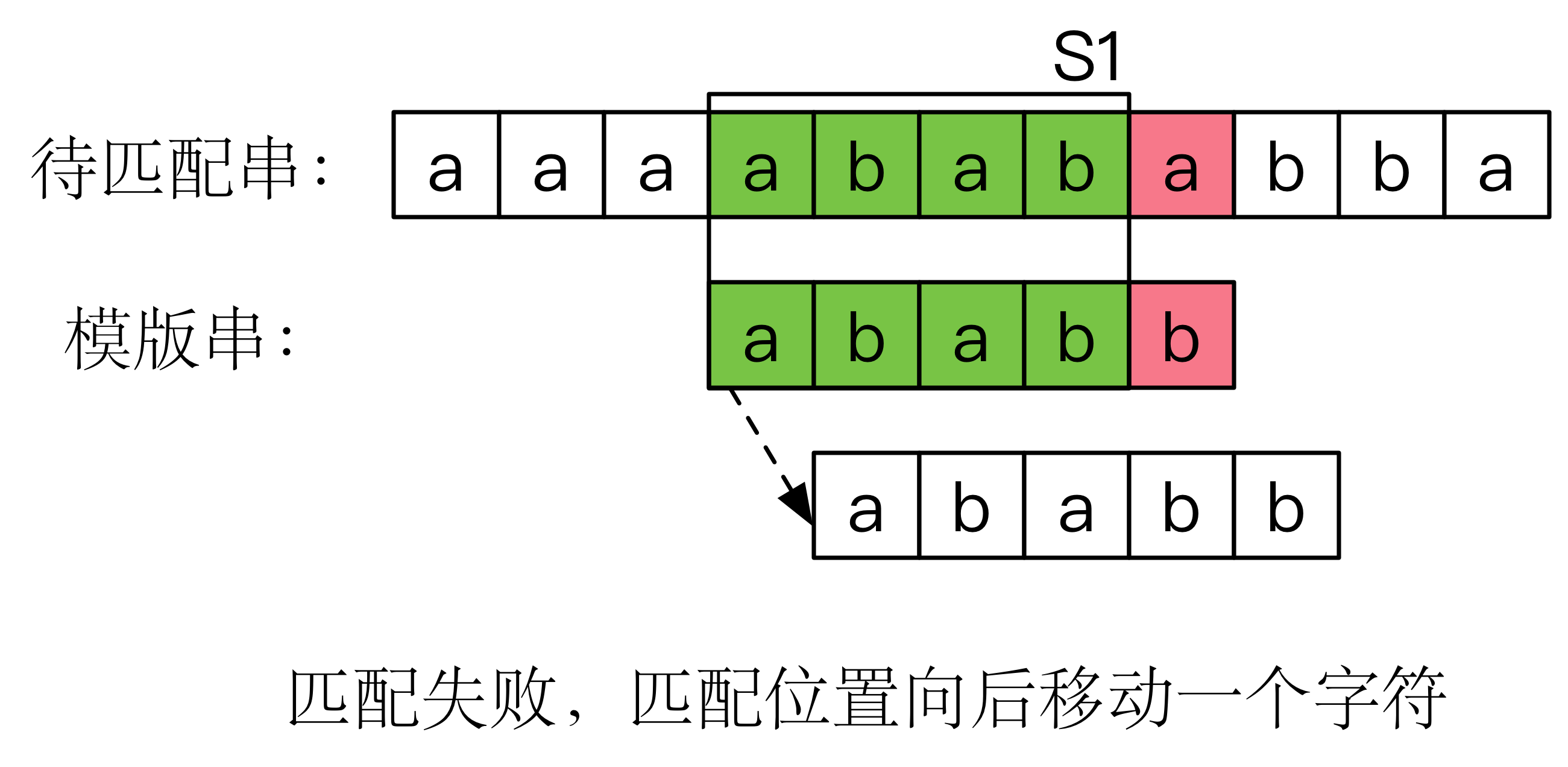
显然,我们可以使用两个指针来分别指向主串和子串的某个字符,依次遍历来实现该算法。
下面是以定长顺序存储表示的字符串下,实现 BF 算法的 C 代码:
1 | int Index(String S, Stirng T){ // S为主串,T为模式串 |
显然 BF 算法在最坏情况下时间复杂度为 ,其中 分别是主串和模式串的长度。
BF 算法在进行模式匹配时,从主串的第一个字符开始,每次失败都是子串后移一位再从头开始比较。而比较过程中的某趟已经匹配相等的字符都是子串的某个前缀,这种频繁的比较相当于子串重复的进行自我比较,这就是其效率低的根源。
以 S = "0000001"; T = "0000000000000000000000000000000000000000000001" 为例,每趟匹配都要比到最后一个字符才发现不符合要求,指针 i 要回退 40 次(S 有 6 个 0,T 有 45 个 0),最后要比较 次才能得出结果。
Knuth-Morria-Pratt 算法
KMP 模式匹配算法是由 D.E.Knuth,J.H.Morris,V.R.Pratt 三人提出的,算法名字就是取得三个作者名字的首字母。(其中第一位就是《计算机程序设计艺术》的作者)
KMP是一种对朴素模式匹配算法的改进,核心就是利用匹配失败后的信息,尽量减少子主串的匹配次数。
利用匹配失败信息
首先我们再次回顾一下朴素模式匹配算法是如何操作的。

显然,这个办法是愚笨的,如果是一个正常人类来匹配的话,他不会仅仅移动一位就继续第二次比较。
因为,既然匹配失败的 b 前面的字符子串(图中区域的 ) abab 已经比较过一次了,那么如果只后移一个字符,接下来再比较第一个字符时, a 与 b 就肯定不会匹配成功。这是还没开始移动,就事先推敲出来的。
但后移两位是可以的,因为 的前两个字符 ab 正好和 的末尾后两个字符 ab 对齐了。如下图所示:
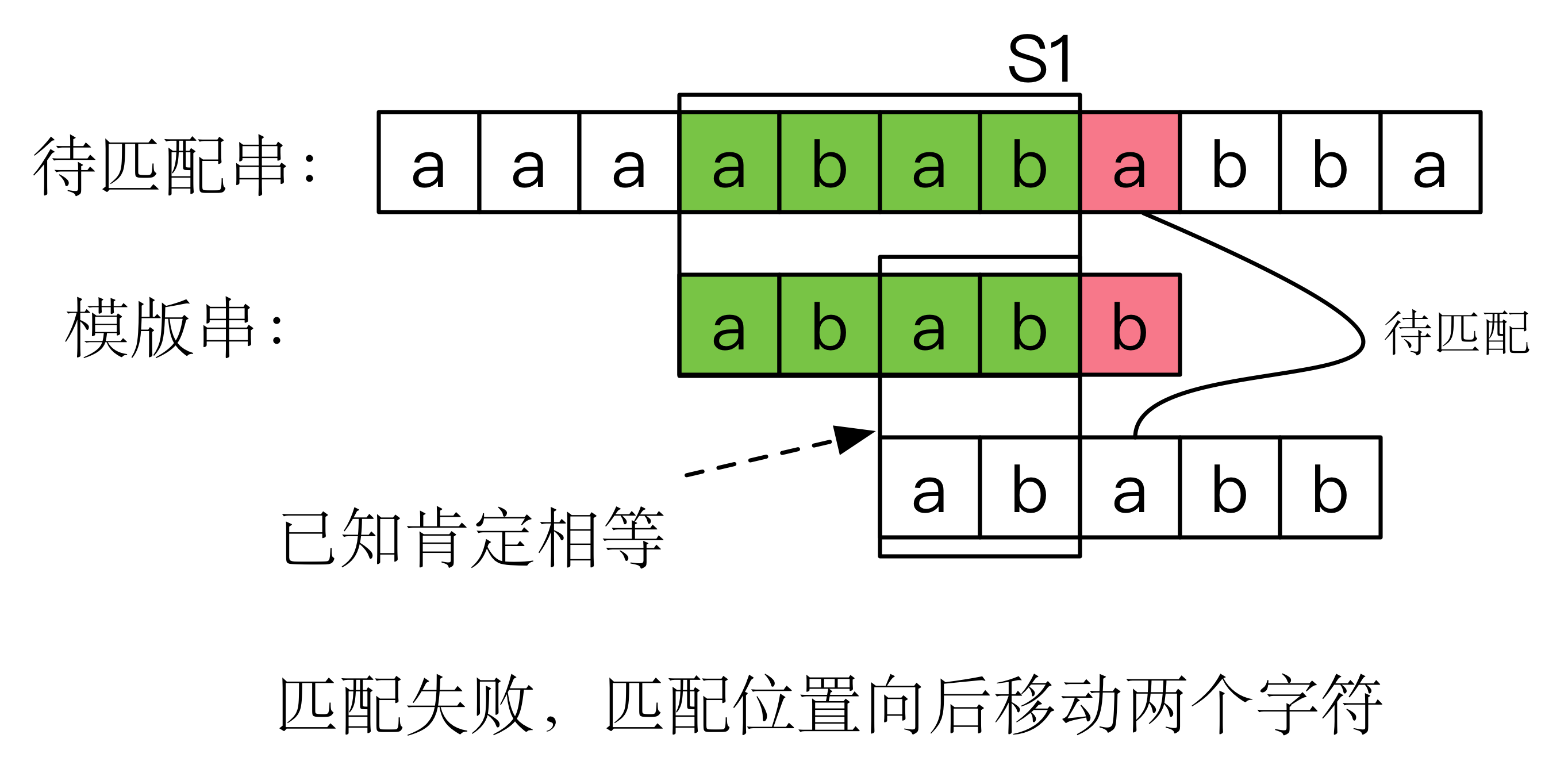
也就是说,我们在进行指针回溯之前,就能够事先根据一些性质确定只移动一位肯定行不通。而上面这个例子中,根据模式串的前缀 ab 和模式串的后缀 ab 一致,所以我们可以确定,它们两个可以对齐,并且可以一次性移动两位,对齐之后再继续后续比较。可以证明,这不会漏情况。
上面这个思路正是 KMP 算法提出的思想。
KMP 算法不仅指出如何判断只移动一位会不会匹配失败,还指出一次性移动多少位可以不漏情况。
这个移动位数,与上面我们提到的”前缀“和”后缀“息息相关。
现作如下规定:
- 前缀 除最后一个字符外,字符串的所有头部子串;
- 后缀 除第一个字符外,字符串的所有尾部子串;
- 部分匹配值 字符串的前缀与后缀相等的最大长度。
以 为例进行说明:
的前缀为 :
的后缀为:
则 的部分匹配值(Partial Match,PM)为:
从而, 时,其长度 最长,故.
前面我们给出的图示中,ab 就是一个最长的前后缀相同的子串,其长度为2,而我们得到的移动位数也正好是2,这二者之间有什么必然联系呢?
可以推导出这样的公式:
我们可以发现, 的值跟主串是没有任何关系的,只要模版串中的失配点确定,那么对应后移的位数也随之确定。
那么,只要我们在匹配之前,事先遍历一次模式串,把它在”已匹配的字符数“为 时的 算出来,就可能直接得到匹配字符达 时需要移动的位数了。
综上所述,KMP 算法可以将时间复杂度降为。
Next 数组的使用
在上一节,我们阐述了移动位数与部分匹配值之间的关系,并且指出只要我们在匹配之前,事先遍历一次模式串,把它在”已匹配的字符数“为 时的 算出来,就可能直接得到匹配字符达 时需要移动的位数了。
注意到,我们在模式串的第 个位置匹配失败,需要取出前 个字符匹配成功情况下得到的 值,然后再按照公式计算得到移动位数 .
既然如此,我们不妨把由 构成的表 整体右移一位,将新表记为 ,则有:
这样一来,当比较到第 个位置匹配失败时,就有:
与失败位置 的具有一一对应关系,所以我们可以利用数组存储,而这就是 Next 数组。
我们知道,在 KMP 算法之中,我们需要在匹配失败之后,将模式串往后移动 步再继续比较。而在编程实现中,实际上并不是将子串移动,而是将比较使用的指针 j 回退。
也就是说,我们不仅用 j 来指示当前比较到了第几个字符,也用 j 的回退来表示移动。
所以,在 j 位置匹配失败之后,应该有 j = j - Move[j],也就是对 赋值:
代入上式,得:
为了更加简洁,我们直接让 的值在原基础上再加一。这样的话,有了 Next 数组,我们在 j 处匹配失败,就将 j 改为 Next[j] 即可!此时:
Next 数组的生成
考虑边界情况,当 j == 1,即第一个就不匹配时, 里的 是没有定义的(空串没有匹配值)。
于是我们规定,Next[1] = 0,表明如果模式串第一个字符就和主串不匹配,那么不移动继续等待主串的指针 i 移动到下一位时,再和模式串比较,这与朴素版算法的行为一样。
考虑另一种边界情况,当 ,即 之前的字符串没有公共的前后缀时,说明没有能够一次性移动的步数,所以只能从头移动,即需要让 回到模式串的起点,使得,所以我们规定此时的 Next[j] = 1 。
综上所述,我们有:
其中, 即是 的值。 是模式串的第 个字符。
上面我们仅给出了 Next 数组的基本框架,当然还有边界情况的取值。而 值究竟怎么算仍然还是问题,接下来我们将进一步解决这个问题。这也是 KMP 算法的精髓。
假设我们已经知道了前 个字符对应的 值,且已知 ,此时我们知道,前 个字符构成的字符串中,前缀取 个,后缀取 个,二者是对应相等的。
用 T[1..j] 表示的话,即有 T[1..k-1] == T[j-k+1..j-1].
现在欲计算 的值。有如下几种情况:
- 当 时,字符串在原本前缀就与后缀匹配的情况下,补上这两个字符之后,实现了前后缀的同步扩充,即
T[1..k] == T[j-k+1..j],所以得到. - 当 时,我们需要找到一个新的值 使得
T[1..k'] = T[j-k'+1..j]。
对于第二种情况,我们需要展开论述。
因为我们要找的新的值 能使得 T[1..k'] = T[j-k'+1..j],所以找 的过程,其实就是一个新的小型的模式匹配问题。即把在原本的前缀 T[1..k] 作为模式串,把包括第 个字符的整个后缀 T[j-k+1..j] 视为主串,企图在新后缀中找到与模式串相重叠的部分,这个长度就是。
显然,因为,所以第一步匹配时一定会失败,并且此时显示前 个字符是匹配成功的,这时,我们需要将作为模式串的 T[1..k] 整体回退到下标为 Next[k] 的位置。
这也就是说,在 T[1..Next[k]-1] 是匹配成功的情况下,对比 T[Next[k]] 的匹配结果,即比较。如果匹配失败,就继续回退到 T[Next[Next[k]]] 的位置。如此往复,直到匹配成功得到 或是匹配失败。失败时我们在上面给了规定,取。
下面给出一个示例,以便更加清晰的理解。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 模式串 | a | b | a | a | b | c | a | b | a |
| 0 | 1 | 1 | 2 | 2 | 3 | ? | ? | ? |
假设已知前 的 值,现求 的 值。
首先,比较. 也就是 T[3] = "a" 和 T[6] = "c" 的值,显然不等。
又因为 ,这说明,即在 之前长为 5 的字符串中,有大小最大是 2 的公共前后缀,即 T[1..2] = "ab" = T[4..5].
前面我们比较的 的结果就是在告诉我们,这两个公共前后缀都往右延伸一位后就发生了不匹配,于是我们需要把 T[1..3] = "aba" 和 T[4..6] = "abc" 分别作为模式串和主串进行模式匹配,以找到新的最长公共前后缀。
因为比较发现前两位是匹配的,而第三位不匹配,所以我们查表,值为1表示此时我们要做的操作是 T[4..6] 不动,将 T[1..3] 的 T[Next[3]] == T[1] 与 T[6] 对齐(也就是说主串不动,从当前位置把模式串从头开始比较)。此时 T[1] 与 T[6] 还是不等,所以查表 ,值为0表示不匹配。所以匹配不成功,也就是此时没有哪怕一个公共前后缀,所以根据我们前面讨论的边界条件情况,我们置.
下面计算.
由于 ,也就是 T[1] = "a" = T[7],匹配成功,所以 。
再计算.
由于 ,也就是 T[2] = "b" = T[8],匹配成功,其实也就是说,在前 位有着长度是 1 的公共前后缀的基础上,往后延伸一位仍然匹配,所以最长公共前后缀的数值增加到2,更进一步,也就是有 。
KMP 算法代码实现
将我们之前的分析利用代码实现如下:
1 | /* 传入模式串,根据模式串返回对应next数组 */ |
Next 数组的改进
前面定义的 Next 数组在某些情况下,其实是有缺陷的,还可以进一步优化。
比如 S = "aaabaaaab", T = "aaaab" 经计算,可得模式串 的 数组如下:
| 模式串 | a | a | a | a | b |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 0 | 1 | 2 | 3 | 4 |
则,当主串的第 4 位与模式串的第 4 位比较时,发现 S[4] = "b" ,T[4] = "a" 二者不等。此时,根据原算法,我们需要比较 S[4], T[Next[4]] == T[3] ,而 T[3] 显然也是与 T[4] 不等的,不仅是因为取出来比较时发现不等,而且因为 T[3] == T[4]。
也就是说,当我们回退 的时候,如果发现 ,那么这个回退其实是没有意义的,我们还得继续回退,白白浪费了一次无意义的比较。
经过上述分析,我们总结得出,如果在 get_next() 阶段,我们就发现回退前后的字符的值相同,那么不如把 值都调整为第一个不相同的值。
比如上面这个例子中,我们依次遍历模式串 时,T[1] = "a",根据边界条件1,我们置 Next[1] = 0。而计算 Next[2] 时,发现正好T[2] == T[1],那么我们也置 Next[2] = 0.
于是,我们得到 Next 数组的改进方法:
1 | /* 改进的next数组获取 */ |
参考
- 串的模式匹配 |CSDN
- KMP算法详细解析
- 《2023王道计算机数据结构》




