动态规划 (Dynamic Programming,DP ) 是运筹学 的一个分支,是求解 决策过程 最优化 的过程。一般情况下,DP问题主要因素都有方向性 和离散性 .
设计方法 应用动态规划方法求解的最优化问题应该具备的两个要素:最优子结构 和子问题重叠 ,此外还要求无后效性。在此基础上,通过对子结构抽象出来的状态以设计状态转移方程 ,用来刻画一个子问题是如何通过其他子问题得到的。
在根据转移方程计算子问题的解时,我们往往建立一张动态规划表 对结果进行保存,在下面的计算中以期直接查表取值。因此,这样的表具有备忘录性质 ,我们也常常称其为备忘录。
最优子结构 用动态规划方法求解最优化问题的第一步就是刻画最优解的结构 。
如果一个问题的最优解包含其子问题的最优解,我们就称此问题具有最优子结构性质 。
某个问题是否具有最优子结构性质,很大程度上决定着它是否适用于动态规划算法(当然,具有最优子结构性质也意味着可能适用与贪心法)。
使用动态规划方法时,我们用子问题的最优解来构造原问题的最优解。因此,我们必须小心确保考察了最优解中用到的所有子问题。 这是至关重要的一步,这关系到备忘录中的值是否切实有效。
子问题重叠 局限性 动态规划对于解决多阶段决策问题的效果是明显的,但是动态规划也有一定的局限性。
首先,它没有统一的处理方法,必须根据问题的各种性质并结合一定的技巧来处理;
另外当变量的维数增大时,总的计算量及存贮量急剧增大。
因而,受计算机的存贮量及计算速度的限制,当今的计算机仍不能用动态规划方法来解决较大规模的问题,这就是“维数障碍 ”.
状态压缩 待更
经典实例一览 最长公共子序列 最优二叉检索树 投资问题 图像压缩算法 最长公共子序列| Longest Common Subsequence 已知序列X = < x 1 , x 2 , . . . , x m > X=<x_1,x_2,...,x_m> X =< x 1 , x 2 , ... , x m > Z = < z 1 , z 2 , . . . , z k > Z=<z_1,z_2,...,z_k> Z =< z 1 , z 2 , ... , z k > 严格递增 的下标序列< i 1 , i 2 , . . . , i k > <i_1,i_2,...,i_k> < i 1 , i 2 , ... , i k > j = 1 , 2 , . . . , k j=1,2,...,k j = 1 , 2 , ... , k x i j = z j x_{i_j}=z_j x i j = z j
< x i 1 , x i 2 , . . . , x i k > = < z 1 , z 2 , . . . , z k > <x_{i_1},x_{i_2},...,x_{i_k}>\;=\;<z_1,z_2,...,z_k> < x i 1 , x i 2 , ... , x i k > = < z 1 , z 2 , ... , z k >
则称Z Z Z X X X 子序列 。
如果序列Z Z Z X X X Y Y Y Z Z Z X , Y X,Y X , Y 公共子序列 。
最长公共子序列 问题 就是对于给定的序列X , Y X,Y X , Y
算法分析 最容易想到的算法自然是暴力穷举法,我们只需把X X X Y Y Y m m m X X X 2 m 2^m 2 m Y Y Y O ( n ) O(n) O ( n ) Y Y Y n n n 指数级 的O ( n 2 m ) O(n2^m) O ( n 2 m )
下面将思考利用动态规划 法求解 LCS 问题。
规定X a X_a X a X X X a a a 连续的元素 构成的子序列,我们称X a X_a X a X X X 前缀 。
从后往前 思考,一个 LCS 问题的求解是否依赖于输入序列X , Y X,Y X , Y 前缀 呢?
假设X = < x 1 , x 2 , . . . , x m > X=<x_1,x_2,...,x_m> X =< x 1 , x 2 , ... , x m > Y = < y 1 , y 2 , . . . , y n > Y=<y_1,y_2,...,y_n> Y =< y 1 , y 2 , ... , y n > Z = < z 1 , z 2 , . . . , z k > Z=<z_1,z_2,...,z_k> Z =< z 1 , z 2 , ... , z k >
当x m = y n x_m=y_n x m = y n z k = x m = y n z_k=x_m=y_n z k = x m = y n Z k − 1 Z_{k-1} Z k − 1 X m − 1 , Y n − 1 X_{m-1},Y_{n-1} X m − 1 , Y n − 1 当x m ≠ y n x_m\neq y_n x m = y n z k = x m z_k=x_m z k = x m Z Z Z X m − 1 , Y X_{m-1},Y X m − 1 , Y 当x m ≠ y n x_m\neq y_n x m = y n z k = y n z_k=y_n z k = y n Z Z Z X , Y n − 1 X,Y_{n-1} X , Y n − 1 不难从上述定理看出,LCS 问题拥有最优子结构,即一个 LCS 问题的求解依赖于输入序列X , Y X,Y X , Y 前缀 。并且通过以上三点,我们已经无形之中划归了子问题:
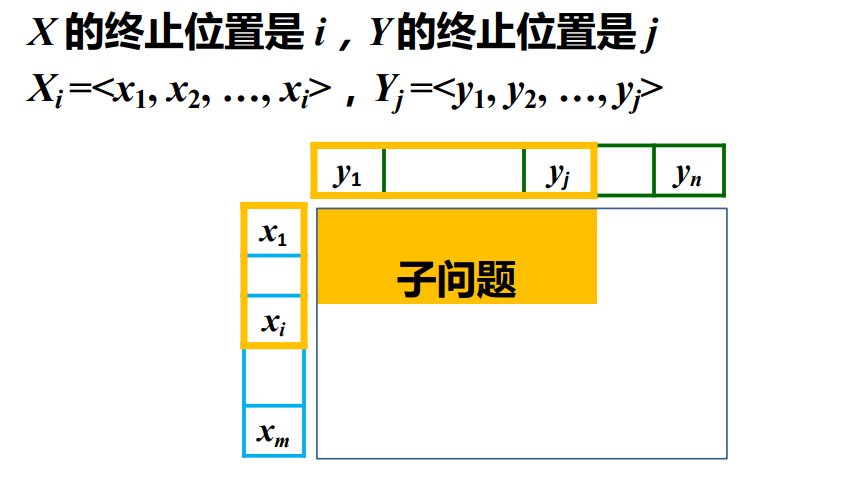
如下图所示,将序列X X X i i i Y Y Y j j j d p ( i , j ) dp(i,j) d p ( i , j )
于是可总结出状态转移方程 .
d p ( i , j ) = { 0 , i = 0 or j = 0 d p ( i − 1 , j − 1 ) + 1 , i , j > 0 and x i = y j max { d p ( i − 1 , j ) , d p ( i , j − 1 ) } , i , j > 0 and x i ≠ y j dp(i,j)=\begin{cases} 0,&i=0\text{ or }j=0\\ dp(i-1,j-1)+1,&i,j\gt0\text{ and }x_i=y_j\\ \max\{dp(i-1,j),dp(i,j-1)\},&i,j\gt0\text{ and }x_i\neq y_j \end{cases} d p ( i , j ) = ⎩ ⎨ ⎧ 0 , d p ( i − 1 , j − 1 ) + 1 , max { d p ( i − 1 , j ) , d p ( i , j − 1 )} , i = 0 or j = 0 i , j > 0 and x i = y j i , j > 0 and x i = y j
如果不仅想要求出 LCS 的长度,而是将 LCS 给出的话,在算法设计时还需要引入标记函数 以进行解的追踪。从状态转移方程对d p ( i , j ) dp(i,j) d p ( i , j )
这里我们规定标记函数为:
B ( i , j ) = { ↖ , d p ( i , j ) = d p ( i − 1 , j − 1 ) + 1 ← , d p ( i , j ) = d p ( i , j − 1 ) ↑ , d p ( i , j ) = d p ( i − 1 , j ) B(i,j)=\begin{cases} ↖,&dp(i,j)=dp(i-1,j-1)+1\\ ←,&dp(i,j)=dp(i,j-1)\\ ↑,&dp(i,j)=dp(i-1,j) \end{cases} B ( i , j ) = ⎩ ⎨ ⎧ ↖ , ← , ↑ , d p ( i , j ) = d p ( i − 1 , j − 1 ) + 1 d p ( i , j ) = d p ( i , j − 1 ) d p ( i , j ) = d p ( i − 1 , j )
伪代码与实现 Algorithm: LCS ( X , Y ) 1. m ← X . l e n g t h 2. n ← Y . l e n g t h 3. f o r i = 1 t o m d o d p [ i , 0 ] ← 0 4. f o r j = 1 t o n d o d p [ 0 , j ] ← 0 5. f o r i = 1 t o m d o 6. f o r j = 1 t o n d o 7. i f x i = y j t h e n 8. d p [ i , j ] ← d p [ i − 1 , j − 1 ] + 1 9. B [ i , j ] ← 【 ↖ 】 10. e l s e i f d p ( i − 1 , j ) ≥ d p ( i , j − 1 ) t h e n 11. d p [ i , j ] ← d p [ i − 1 , j ] 12. B [ i , j ] ← 【 ↑ 】 13. e l s e 14. d p [ i , j ] ← d p [ i , j − 1 ] 15. B [ i , j ] ← 【 ← 】 16. r e t u r n d p [ m , n ] , B \begin{aligned} &\text{Algorithm: }\;\text{LCS}(X,Y)\\\\ 1.&\;m\leftarrow X.length\\ 2.&\;n\leftarrow Y.length\\ 3.&\;\mathbf{for}\;i\;=1\;\mathbf{to}\;m\;\mathbf{do}\;dp[i,0]\leftarrow0\\ 4.&\;\mathbf{for}\;j\;=1\;\mathbf{to}\;n\;\mathbf{do}\;dp[0,j]\leftarrow0\\ 5.&\;\mathbf{for}\;i\;=1\;\mathbf{to}\;m\;\mathbf{do}\\ 6.&\;\qquad\mathbf{for}\;j\;=1\;\mathbf{to}\;n\;\mathbf{do}\\ 7.&\;\qquad\qquad\mathbf{if}\;x_i=y_j\;\mathbf{then}\\ 8.&\;\qquad\qquad\qquad dp[i,j]\leftarrow dp[i-1,j-1]+1\\ 9.&\;\qquad\qquad\qquad B[i,j]\leftarrow 【↖】\\ 10.&\;\qquad\qquad\mathbf{else\;if}\;dp(i-1,j)\geq dp(i,j-1)\;\mathbf{then}\\ 11.&\;\qquad\qquad\qquad dp[i,j]\leftarrow dp[i-1,j]\\ 12.&\;\qquad\qquad\qquad B[i,j]\leftarrow 【↑】\\ 13.&\;\qquad\qquad\mathbf{else}\\ 14.&\;\qquad\qquad\qquad dp[i,j]\leftarrow dp[i,j-1]\\ 15.&\;\qquad\qquad\qquad B[i,j]\leftarrow 【←】\\ 16.&\;\mathbf{return}\;dp[m,n],B \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. Algorithm: LCS ( X , Y ) m ← X . l e n g t h n ← Y . l e n g t h for i = 1 to m do d p [ i , 0 ] ← 0 for j = 1 to n do d p [ 0 , j ] ← 0 for i = 1 to m do for j = 1 to n do if x i = y j then d p [ i , j ] ← d p [ i − 1 , j − 1 ] + 1 B [ i , j ] ← 【 ↖ 】 else if d p ( i − 1 , j ) ≥ d p ( i , j − 1 ) then d p [ i , j ] ← d p [ i − 1 , j ] B [ i , j ] ← 【 ↑ 】 else d p [ i , j ] ← d p [ i , j − 1 ] B [ i , j ] ← 【 ← 】 return d p [ m , n ] , B
解的追溯将在下面的 c++ 实现中给出具体的递归调用实现。
分析伪代码可知,该算法的时间复杂度为O ( m n ) O(mn) O ( mn ) O ( m n ) O(mn) O ( mn )
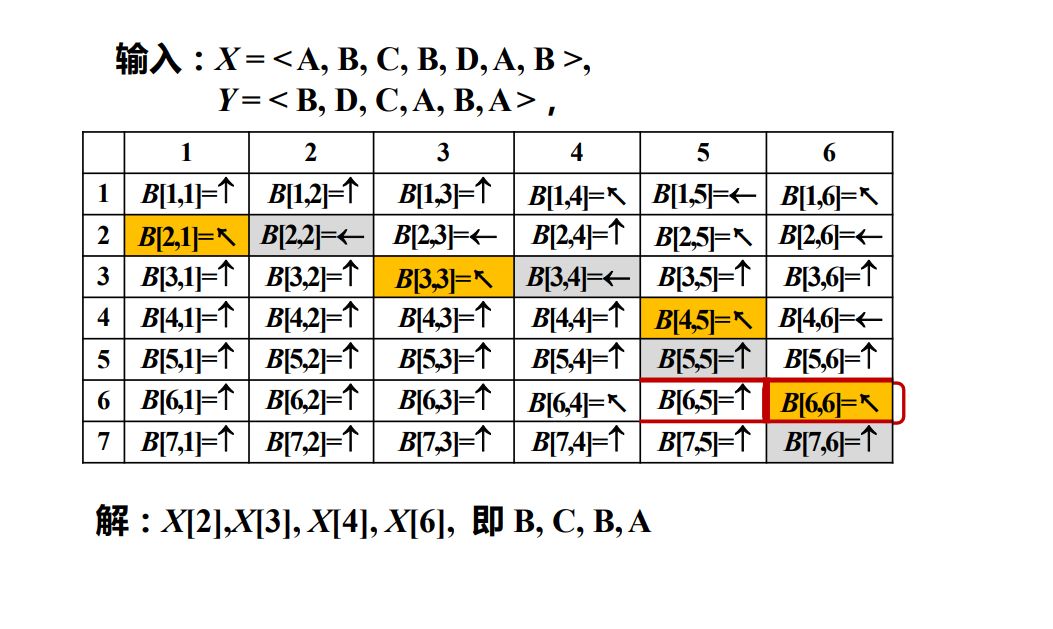
以输入X = < A , B , C , B , D , A , B > , Y = < B , D , C , A , B , A > X =<A, B, C, B, D, A, B> , Y = < B, D, C,A, B,A> X =< A , B , C , B , D , A , B > , Y =< B , D , C , A , B , A >
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 #define M 128 int dp[M][M];int mark[M][M]; int Len (int p) int res = 0 ; while (p){ res++; p = p/2 ; } return res; } int LCS (char X[], char Y[]) int m = strlen (X); int n = strlen (Y); memset (dp,0 ,sizeof (dp)); memset (mark,0 ,sizeof (mark)); for (int i = 1 ; i <= m; i++) dp[i][0 ] = 0 ; for (int j = 1 ; j <= n; j++) dp[0 ][j] = 0 ; for (int i = 1 ; i <= m; i++){ for (int j = 1 ; j <= n; j++){ if (X[i-1 ] == Y[j-1 ]){ dp[i][j] = dp[i-1 ][j-1 ]+1 ; mark[i][j] = 2 ; }else if (dp[i-1 ][j] >= dp[i][j-1 ]){ dp[i][j] = dp[i-1 ][j]; mark[i][j] = 1 ; }else { dp[i][j] = dp[i][j-1 ]; mark[i][j] = -1 ; } } } return dp[m][n]; } void Traceback (char X[], int m, int n) if (mark[m][n] == 2 ){ Traceback (X, m-1 , n-1 ); cout << X[m-1 ] << " " ; }else if (mark[m][n] == -1 ){ Traceback (X, m, n-1 ); }else if (mark[m][n] == 1 ){ Traceback (X, m-1 , n); }else { return ; } } int main (void ) char A[] = "ABCBDAB" ; char B[] = "BDCABA" ; cout << "min Length = " << LCS (A,B) << endl << endl; Traceback (A, 7 , 6 ); cout << "END" << endl; while (1 ); }
最终的输出结果如下:
投资问题| Investment Problem 投资问题是运筹学 和数学中一种很经典的数学规划模型。
假设拥有m m m n n n x x x i i i f i ( x ) f_i(x) f i ( x )
可对该问题建立 非线性整数规划模型 :
max ∑ i = 1 n f i ( x i ) s . t . { ∑ i = 1 n x i ≤ m x i ∈ N , i = 1 , 2 , . . , n \begin{aligned} \max &\sum_{i=1}^nf_i(x_i)\\ s.t.&\begin{cases} \sum\limits_{i=1}^nx_i\leq m\\ x_i\in N,i=1,2,..,n \end{cases} \end{aligned} max s . t . i = 1 ∑ n f i ( x i ) ⎩ ⎨ ⎧ i = 1 ∑ n x i ≤ m x i ∈ N , i = 1 , 2 , .. , n
式中,x i x_i x i i i i
状态转移方程 思考本问题的输入,要求对给定金额m m m n n n m , n m,n m , n d p ( m , n ) dp(m,n) d p ( m , n )
从前向后 思考.
当金额为 1 ,可选项目为 1 时,显然将所有金额投入给该项目可获得最大收益,即d p ( 1 , 1 ) = f 1 ( 1 ) dp(1,1)=f_1(1) d p ( 1 , 1 ) = f 1 ( 1 ) x x x d p ( x , 1 ) = f 1 ( x ) dp(x,1)=f_1(x) d p ( x , 1 ) = f 1 ( x ) 当金额为 2,可选项目为 2 时,可能的选择有:将 1 元投给项目 1,将 1 元投给项目 2; 将全部 2 元都投给项目 1; 将全部 2 元都投给项目 2.取最大 则为最优解。d p ( 2 , 2 ) = max { d p ( 1 , 1 ) + f 2 ( 1 ) , d p ( 2 , 1 ) + f 2 ( 0 ) , d p ( 0 , 1 ) + f 2 ( 2 ) } dp(2,2)=\max\{dp(1,1)+f_2(1),dp(2,1)+f_2(0),dp(0,1)+f_2(2)\} d p ( 2 , 2 ) = max { d p ( 1 , 1 ) + f 2 ( 1 ) , d p ( 2 , 1 ) + f 2 ( 0 ) , d p ( 0 , 1 ) + f 2 ( 2 )} 依次类推,则可得到完整的状态转移方程 :
d p ( m , n ) = { max 0 ≤ x ≤ m { d p ( x , n − 1 ) + f n ( m − x ) } , n > 1 f 1 ( m ) , n = 1 dp(m,n)=\begin{cases} \max\limits_{0\leq x\leq m}\{dp(x,n-1)+f_n(m-x)\},&n\gt1\\\\ f_1(m),&n=1 \end{cases} d p ( m , n ) = ⎩ ⎨ ⎧ 0 ≤ x ≤ m max { d p ( x , n − 1 ) + f n ( m − x )} , f 1 ( m ) , n > 1 n = 1
根据动态规划的备忘录 性质,均利用二维数组对结果进行存储,进而得到伪码.
输入:m , n , f [ 1.. n , 1.. m ] m,n,f[1..n,1..m] m , n , f [ 1.. n , 1.. m ] i i i j j j 输出:最大收益 Algorithm: Investment ( m , n , f ) 1. r e p e a t d p [ j , i ] ← 0 u n t i l dp初始化完毕 2. f o r i = 1 t o n d o 3. f o r j = 0 t o m d o 4. f o r k = 0 t o j d o 5. d p [ j , i ] ← max ( d p [ j , i ] , d p [ k , i − 1 ] + f [ i , j − k ] ) 6. r e t u r n d p [ m , n ] \begin{aligned} &\text{Algorithm: }\;\text{Investment}(m,n,f)\\\\ 1.&\;\mathbf{repeat}\;dp[j,i]\leftarrow 0\;\mathbf{until}\;\text{dp初始化完毕}\\ 2.&\;\mathbf{for}\;i\;=1\;\mathbf{to}\;n\;\mathbf{do}\\ 3.&\;\qquad\mathbf{for}\;j\;=0\;\mathbf{to}\;m\;\mathbf{do}\\ 4.&\;\qquad\qquad\mathbf{for}\;k\;=0\;\mathbf{to}\;j\;\mathbf{do}\\ 5.&\;\qquad\qquad\qquad dp[j,i]\leftarrow \text{max}(dp[j,i],dp[k,i-1]+f[i,j-k])\\ 6.&\;\mathbf{return}\;dp[m,n] \end{aligned} 1. 2. 3. 4. 5. 6. Algorithm: Investment ( m , n , f ) repeat d p [ j , i ] ← 0 until dp 初始化完毕 for i = 1 to n do for j = 0 to m do for k = 0 to j do d p [ j , i ] ← max ( d p [ j , i ] , d p [ k , i − 1 ] + f [ i , j − k ]) return d p [ m , n ]
显然,对于最内层循环,需要执行j + 1 j+1 j + 1 j j j j : 0 → m j:0\to m j : 0 → m n n n T ( m , n ) = ∑ i = 1 n ∑ j = 0 m [ ( j + 1 ) + j ] = O ( n m 2 ) \begin{aligned}T(m,n)=\sum_{i=1}^n\sum_{j=0}^m[(j+1)+j]=O(nm^2)\end{aligned} T ( m , n ) = i = 1 ∑ n j = 0 ∑ m [( j + 1 ) + j ] = O ( n m 2 ) O ( n m ) O(nm) O ( nm )
解的追溯 除了计算最大收益之外,还可以在算法中建立一个标记矩阵从而得以追溯使得最大收益成立的具体决策。
设置标记m a r k [ i , j ] mark[i,j] ma r k [ i , j ] j j j i i i j − 1 j-1 j − 1
x n = m − m a r k [ m , n ] x n − 1 = ( m − x n ) − m a r k [ x n , n − 1 ] x n − 2 = ( m − x n − x n − 1 ) − m a r k [ x n − 1 , n − 2 ] ⋯ = ⋯ x 1 = ( m − ∑ k = 2 n x k ) − m a r k [ x 2 , 1 ] \begin{aligned} x_n&=m-mark[m,n]\\ x_{n-1}&=(m-x_n)-mark[x_n,n-1]\\ x_{n-2}&=(m-x_n-x_{n-1})-mark[x_{n-1},n-2]\\ \cdots&=\cdots\\ x_1&=(m-\sum_{k=2}^nx_k)-mark[x_2,1] \end{aligned} x n x n − 1 x n − 2 ⋯ x 1 = m − ma r k [ m , n ] = ( m − x n ) − ma r k [ x n , n − 1 ] = ( m − x n − x n − 1 ) − ma r k [ x n − 1 , n − 2 ] = ⋯ = ( m − k = 2 ∑ n x k ) − ma r k [ x 2 , 1 ]
实例展示与代码 假设给定如下数据,其中手持金额m = 5 m=5 m = 5 n = 4 n=4 n = 4 i i i x x x f i ( x ) f_i(x) f i ( x )
x x x f 1 [ x ] f_1[x] f 1 [ x ] f 2 [ x ] f_2[x] f 2 [ x ] f 3 [ x ] f_3[x] f 3 [ x ] f 4 [ x ] f_4[x] f 4 [ x ] 0 0 0 0 0 1 11 0 2 20 2 12 5 10 21 3 13 10 30 22 4 14 15 32 23 5 15 20 40 24
下面先给出对该问题的 C++ 编程实现 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #define M 20 int f[5 ][6 ] = {{0 ,0 ,0 ,0 ,0 ,0 }, {0 ,11 ,12 ,13 ,14 ,15 }, {0 ,0 ,5 ,10 ,15 ,20 }, {0 ,2 ,10 ,30 ,32 ,40 }, {0 ,20 ,21 ,22 ,23 ,24 }}; int mark[M][M];int Inverstment (int m, int n) int dp[M][M]; memset (dp,0 ,sizeof (dp)); memset (mark,0 ,sizeof (mark)); for (int i = 1 ; i <= n; i++){ for (int j = 0 ; j <= m; j++){ for (int k = 0 ; k <= j; k++){ if (dp[k][i-1 ]+f[i][j-k] > dp[j][i]){ dp[j][i] = dp[k][i-1 ]+f[i][j-k]; mark[j][i] = k; } } } } return dp[m][n]; } void get_solve (int m, int n) vector<int > X = vector <int >(n); for (int i = n-1 ; i >= 0 ; i--){ X[i] = m-mark[m][i+1 ]; m = mark[m][i+1 ]; } for (int i = 0 ; i < X.size (); i++){ cout << "x" << i+1 << "=" << X[i] << endl; } }
根据算法构建备忘录表格:
x x x d p [ x ] [ 1 ] , m a r k [ x ] [ 1 ] dp[x][1],mark[x][1] d p [ x ] [ 1 ] , ma r k [ x ] [ 1 ] d p [ x ] [ 2 ] , m a r k [ x ] [ 2 ] dp[x][2],mark[x][2] d p [ x ] [ 2 ] , ma r k [ x ] [ 2 ] d p [ x ] [ 3 ] , m a r k [ x ] [ 3 ] dp[x][3],mark[x][3] d p [ x ] [ 3 ] , ma r k [ x ] [ 3 ] d p [ x ] [ 4 ] , m a r k [ x ] [ 4 ] dp[x][4],mark[x][4] d p [ x ] [ 4 ] , ma r k [ x ] [ 4 ] 0 0, 0 0, 0 0, 0 0, 0 1 11, 0 11, 1 11, 1 20, 0 2 12, 0 12, 2 13, 1 31, 1 3 13, 0 16, 1 30, 0 33, 2 4 14, 0 21, 1 41, 1 50, 3 5 15, 0 26, 1 43, 1 61, 4
从而,d p [ 5 ] [ 4 ] = 61 dp[5][4]=61 d p [ 5 ] [ 4 ] = 61 最大收益 。
根据标记的回溯原则,可以分别得到:( x 1 , x 2 , x 3 , x 4 ) = ( 1 , 0 , 3 , 1 ) (x_1,x_2,x_3,x_4)=(1,0,3,1) ( x 1 , x 2 , x 3 , x 4 ) = ( 1 , 0 , 3 , 1 )
代码的运行结果也正是如此:
1 2 3 4 5 6 7 8 max:61 x1=1 x2=0 x3=3 x4=1
变位压缩| Variable Identification Compression 本问题取自 中国大学MOOC 由北京大学的屈婉玲 教授讲解的 动态规划 一节里的经典例题。
能力有限,我只找到这种特殊的图像变位压缩方法最早出现在 2001年版《计算机算法设计与分析》(王晓东 箸)一书中, 该书涉及的算法示例颇多,并且MOOC上的例题基本出自此书。后来才得知,屈婉玲老师于2011年出版的《算法设计与分析》正是在该书的基础上改进了很多饱受诟病的语言描述和字符混乱问题,并且结合《算法导论》增加了问题的正确性证明,加深了数学语言的表示。
不过对于本节的数字图像变位压缩问题,还是溯源无果,因此此处的英文名取自同样引用王晓东一书的期刊文献:
[1]丁爱芬, 周华君, 石宜金. 一种基于变位与反转变换的动态规划压缩算法[J]. 西南师范大学学报:自然科学版, 2020, 45(1):5.
技术描述 给定一幅灰度图,其像素个数为n n n n n n { p 1 , p 2 , . . . , p n } \{p_1,p_2,...,p_n\} { p 1 , p 2 , ... , p n } ∀ p i , p i ∈ [ 0 : 1 : 255 ] \forall p_i,\;p_i\in[0:1:255] ∀ p i , p i ∈ [ 0 : 1 : 255 ] 8 n b i t 8n\;bit 8 n bi t { p 1 , p 2 , . . . , p n } \{p_1,p_2,...,p_n\} { p 1 , p 2 , ... , p n }
下给出一种变位的压缩思想对该序列实现无损压缩。其主要思想是:
将序列分为m m m S 1 , S 2 , . . . , S m S_1,S_2,...,S_m S 1 , S 2 , ... , S m ⋃ i = 1 m S i = { p 1 , p 2 , . . . , p n } \bigcup\limits_{i=1}^m S_i=\{p_1,p_2,...,p_n\} i = 1 ⋃ m S i = { p 1 , p 2 , ... , p n } 段S i S_i S i k k k p k ( i ) p_k^{(i)} p k ( i ) S i S_i S i l i l_i l i 对∀ p k ( i ) ∈ S i \forall p_k^{(i)}\in S_i ∀ p k ( i ) ∈ S i h i ≤ 8 h_i\leq 8 h i ≤ 8 则h i h_i h i h i h_i h i
选出S i S_i S i p k ( i ) p_k^{(i)} p k ( i ) h i h_i h i
h i = ⌈ log 2 ( max p k ( i ) ∈ S i p k ( i ) + 1 ) ⌉ ≤ 8 h_i=\left \lceil\log_2\left(\max\limits_{p_k^{(i)} \in S_i}{p_k^{(i)}}+1\right)\right\rceil\leq 8 h i = ⌈ log 2 ( p k ( i ) ∈ S i max p k ( i ) + 1 ) ⌉ ≤ 8
那么 对于S i S_i S i h i h_i h i
为了让计算机知道每一个分段下具体有几个像素,灰度值用几位表示,本算法规定对每一段S i S_i S i 段头 都先用 11 位的标志位 来记录本段的存储情况.l i l_i l i h i h_i h i
也就是说,任意一段S i S_i S i 11 + h i × l i 11+h_i\times l_i 11 + h i × l i
从而,最优 的压缩就是寻找到这样一种分段策略T = { S 1 , S 2 , ⋯ , S m } T=\{S_1,S_2,\cdots,S_m\} T = { S 1 , S 2 , ⋯ , S m } 存储位数最小 。即:
max T ∑ i = 1 m ( 11 + h i l i ) \max_{T}\sum_{i=1}^m(11+h_il_i) T max i = 1 ∑ m ( 11 + h i l i )
状态转移方程 考虑从p 1 p_1 p 1 p i p_i p i i i i d p ( i ) dp(i) d p ( i )
从后往前 思考,假设已知d p ( 1 ) ⋯ d p ( i − 1 ) dp(1)\cdots dp(i-1) d p ( 1 ) ⋯ d p ( i − 1 )
末尾的单像素{ p i } \{p_{i}\} { p i } S m S_m S m d p ( i − 1 ) dp(i-1) d p ( i − 1 ) T ′ = { S 1 , S 2 , . . . , S m − 1 } T'=\{S_1,S_2,...,S_{m-1}\} T ′ = { S 1 , S 2 , ... , S m − 1 } T = { S 1 , S 2 , ⋯ , S m } T=\{S_1,S_2,\cdots,S_m\} T = { S 1 , S 2 , ⋯ , S m } 末尾的两个像素{ p i − 1 , p i } \{p_{i-1},p_i\} { p i − 1 , p i } S m S_m S m d p ( i − 2 ) dp(i-2) d p ( i − 2 ) T ′ = { S 1 , S 2 , . . . , S m − 1 } T'=\{S_1,S_2,...,S_{m-1}\} T ′ = { S 1 , S 2 , ... , S m − 1 } T = { S 1 , S 2 , ⋯ , S m } T=\{S_1,S_2,\cdots,S_m\} T = { S 1 , S 2 , ⋯ , S m } 末尾的3个像素{ p i − 2 , p i − 1 , p i } \{p_{i-2},p_{i-1},p_i\} { p i − 2 , p i − 1 , p i } S m S_m S m d p ( i − 2 ) dp(i-2) d p ( i − 2 ) T ′ = { S 1 , S 2 , . . . , S m − 1 } T'=\{S_1,S_2,...,S_{m-1}\} T ′ = { S 1 , S 2 , ... , S m − 1 } T = { S 1 , S 2 , ⋯ , S m } T=\{S_1,S_2,\cdots,S_m\} T = { S 1 , S 2 , ⋯ , S m } ...将整个序列{ p 1 , p 2 , . . . , p i } \{p_1,p_2,...,p_i\} { p 1 , p 2 , ... , p i } d p ( 0 ) = 0 dp(0)=0 d p ( 0 ) = 0 11 tag S S m h[i-j+1, i]×j dp[i-j] S m 1 ... 如图所示,对于上述的第j j j
d p ( i − j ) + h ( i − j + 1 , i ) × j + 11 dp(i-j)+h(i-j+1,i)\times j+11 d p ( i − j ) + h ( i − j + 1 , i ) × j + 11
其中,h ( i − j + 1 , i ) h(i-j+1,i) h ( i − j + 1 , i ) j j j S m S_m S m h m h_m h m
h m = ⌈ log 2 ( max p k ( m ) ∈ S m p k ( m ) + 1 ) ⌉ = ⌈ log 2 ( max i − j + 1 ≤ k ≤ i p k + 1 ) ⌉ = h ( i − j + 1 , i ) \begin{aligned} h_m&=\left \lceil\log_2\left(\max\limits_{p_k^{(m)} \in S_m}{p_k^{(m)}}+1\right)\right\rceil\\ &=\left \lceil\log_2\left(\max\limits_{i-j+1\leq k\leq i}{p_k}+1\right)\right\rceil=h(i-j+1,i) \end{aligned} h m = ⌈ log 2 ( p k ( m ) ∈ S m max p k ( m ) + 1 ) ⌉ = ⌈ log 2 ( i − j + 1 ≤ k ≤ i max p k + 1 ) ⌉ = h ( i − j + 1 , i )
所以,我们只需搜索所有可能的分割点j : 1 → min { i , 256 } j:1\to \min\{i,256\} j : 1 → min { i , 256 } d p ( i ) dp(i) d p ( i )
最终得到状态转移方程如下:
d p ( i ) = { min 1 ≤ j ≤ i { d p ( i − j ) + h ( i − j + 1 , i ) × j + 11 } , n ≥ 1 0 , n = 0 dp(i)=\begin{cases} \min\limits_{1\leq j\leq i}\{dp(i-j)+h(i-j+1,i)\times j+11\},&n\geq1\\ 0,&n=0 \end{cases} d p ( i ) = { 1 ≤ j ≤ i min { d p ( i − j ) + h ( i − j + 1 , i ) × j + 11 } , 0 , n ≥ 1 n = 0
伪码与性能分析 分析转移方程可知,d p ( n ) dp(n) d p ( n ) d p ( 1.. n − 1 ) dp(1..n-1) d p ( 1.. n − 1 ) d p [ 0.. n ] dp[0..n] d p [ 0.. n ] i : 1 → n i:1\to n i : 1 → n
为了追溯划分策略 ,还可以建立一维数组s p l i t [ 1.. n ] split[1..n] s pl i t [ 1.. n ] i i i
为了避免繁琐的计算,算法对输入的数组p [ 1.. n ] p[1..n] p [ 1.. n ] h [ 1.. n ] h[1..n] h [ 1.. n ] h [ i ] h[i] h [ i ] p i p_i p i h [ i ] = ⌈ log 2 ( p [ i ] + 1 ) ⌉ h[i]=\left \lceil\log_2\left(p[i]+1\right)\right\rceil h [ i ] = ⌈ log 2 ( p [ i ] + 1 ) ⌉
所以,对于转移方程中的h ( i − j + 1 , i ) h(i-j+1,i) h ( i − j + 1 , i ) h m a x hmax hma x
算法伪码如下:
Algorithm: Compression ( p , n ) 1. 初始化数组 d p , s p l i t 2. d p [ 0 ] ← 0 3. f o r i = 1 t o n d o 4. h m a x ← h [ i ] ← ⌈ log 2 ( p [ i ] + 1 ) ⌉ 5. d p [ i ] ← d p [ i − 1 ] + h m a x 6. s p l i t [ i ] ← 1 7. f o r j = 2 t o min { i , 256 } d o 8. h m a x ← max ( h m a x , h [ i − j + 1 ] ) 9. t m p ← d p [ i − j ] + j × h m a x 10. i f t m p < d p [ i ] t h e n 11. d p [ i ] ← t m p 12. s p l i t [ i ] ← j 13. d p [ i ] ← d p [ i ] + 11 14. r e t u r n d p , s p l i t \begin{aligned} &\text{Algorithm: }\;\text{Compression}(p,n)\\\\ 1.&\;\text{初始化数组 }dp,\;split\\ 2.&\;dp[0]\leftarrow0\\ 3.&\;\mathbf{for}\;i\;=1\;\mathbf{to}\;n\;\mathbf{do}\\ 4.&\;\qquad hmax\leftarrow h[i]\leftarrow\left \lceil\log_2\left(p[i]+1\right)\right\rceil\\ 5.&\;\qquad dp[i]\leftarrow dp[i-1]+hmax\\ 6.&\;\qquad split[i]\leftarrow 1\\ 7.&\;\qquad\mathbf{for}\;j\;=2\;\mathbf{to}\;\min\{i,256\}\;\mathbf{do}\\ 8.&\;\qquad\qquad hmax\leftarrow \max(hmax,h[i-j+1])\\ 9.&\;\qquad\qquad tmp\leftarrow dp[i-j]+j\times hmax\\ 10.&\;\qquad\qquad \mathbf{if}\;tmp\lt dp[i]\;\mathbf{then}\\ 11.&\;\qquad\qquad\qquad dp[i]\leftarrow tmp\\ 12.&\;\qquad\qquad\qquad split[i]\leftarrow j\\ 13.&\;\qquad\qquad dp[i]\leftarrow dp[i]+11\\ 14.&\;\mathbf{return}\;dp,\;split \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. Algorithm: Compression ( p , n ) 初始化数组 d p , s pl i t d p [ 0 ] ← 0 for i = 1 to n do hma x ← h [ i ] ← ⌈ log 2 ( p [ i ] + 1 ) ⌉ d p [ i ] ← d p [ i − 1 ] + hma x s pl i t [ i ] ← 1 for j = 2 to min { i , 256 } do hma x ← max ( hma x , h [ i − j + 1 ]) t m p ← d p [ i − j ] + j × hma x if t m p < d p [ i ] then d p [ i ] ← t m p s pl i t [ i ] ← j d p [ i ] ← d p [ i ] + 11 return d p , s pl i t
【注】一些说明:
伪码中的j j j 2 开始的。这是因为在 4 至 6 行 我们直接对j = 1 j=1 j = 1 因为转移方程中存在常数 11,它不影响比较,因此统一将 11 放到一次大循环后添加(第 13 行) 第 4 行的h [ i ] h[i] h [ i ] i i i h m a x hmax hma x i i i j j j p i p_i p i h m a x hmax hma x p i − j + 1 p_{i-j+1} p i − j + 1 由于j j j 256 256 256 n n n n n n j j j W ( n ) = 256 = O ( 1 ) W(n)=256=O(1) W ( n ) = 256 = O ( 1 ) i i i n n n O ( n ) O(n) O ( n )
根据备忘录的大小可知,本算法的空间复杂度应为O ( n ) O(n) O ( n )
编程实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 #define M 256+1 int dp[M];int split[M];int Len (int p) int res = 0 ; while (p){ res++; p = p/2 ; } return res; } int Compression (int p[], int n) memset (dp,0 ,sizeof (dp)); memset (split,0 ,sizeof (split)); int h[M] = {0 }; int hmax = 0 ; dp[0 ] = 0 ; for (int i = 1 ; i <= n; i++){ h[i] = Len (p[i]); hmax = h[i]; dp[i] = dp[i-1 ]+hmax; split[i] = i; for (int j = 2 ; j <= min (i,256 ); j++){ hmax = max (hmax,h[i-j+1 ]); int tmp = dp[i-j]+j*hmax; if (dp[i] > tmp){ dp[i] = tmp; split[i] = j; } } dp[i] += 11 ; } return dp[n]; } void Traceback (int n) int i = 1 ; int right = n; int left = right-split[right]+1 ; while (right){ cout << "group " << i << ": (" << left << ", " << right << ")" << endl; right = left-1 ; left = right-split[right]+1 ; i++; } }
输出结果如下:
1 2 3 4 min bit = 57 group 1 : (5 , 6 ) group 2 : (1 , 4 )
表示将 [1-4] 分为一组,[5-6]分为一组时,可使得存储位数最小,且最小为57位。
数塔问题 HDU
贪心 暴力 O(2^n) DP O(n^2/2) 免费馅饼
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <iostream> #include <string.h> using namespace std;int maxof3 (int a,int b,int c) int tmp = max (a,b); return max (tmp,c); } int dp[100001 ][12 ];int main (void ) int n; int x,y,x_max=0 ; int i,j; while (cin >> n){ if (n == 0 ) return -1 ; memset (dp,0 ,sizeof (dp)); for (i = 0 ; i < n; i++){ scanf ("%d%d" ,&y,&x); dp[x][y]++; x_max = max (x_max,x); } for (i=x_max;i>0 ;i--) { for (j=0 ;j<=10 ;j++) dp[i-1 ][j]+=maxof3 (dp[i][j],dp[i][j+1 ],dp[i][j-1 ]); } cout << dp[0 ][5 ] << endl; } return 0 ; }
搬寝室
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <iostream> #include <string.h> #include <stdio.h> #include <algorithm> #define inf 0x3f3f3f3f using namespace std;int dp[2000 ][1000 ];int main (void ) int n,k; int i,j; int a[2000 ]; while (~scanf ("%d%d" ,&n,&k)){ memset (a,0 ,sizeof (a)); memset (dp,inf,sizeof (dp)); for (i = 0 ; i < n; i++){ scanf ("%d" ,&a[i]); } sort (a,a+n); dp[0 ][0 ]=dp[1 ][0 ]=0 ; dp[2 ][1 ] = (a[0 ]-a[1 ])*(a[0 ]-a[1 ]); for (i = 2 ; i <= n; i++){ dp[i][0 ]=0 ; for (j = 1 ; j <= k; j++){ dp[i][j] = min (dp[i-1 ][j],dp[i-2 ][j-1 ]+(a[i-1 ]-a[i-2 ])*(a[i-1 ]-a[i-2 ])); } } cout << dp[n][k] << endl; } return 0 ; }
最长上升子序列 小规模
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <bits/stdc++.h> using namespace std;typedef long long LL;const LL maxn = 1000010 ;const LL mod = 1000000007 ;LL a[maxn]; int dp[maxn];#define CPC int main (void ) #ifdef CPC char bufin[40012 ],bufout[40012 ]; for (int t = 1 ; t <= 1 ; t++){ sprintf (bufin,"%02d.in" , t); sprintf (bufout,"%02d.out2" ,t); freopen (bufin,"rb" , stdin); freopen (bufout, "wb" , stdout); #endif LL n, b; while (~scanf ("%lld%lld" ,&n,&b)) { a[1 ] = b; dp[1 ] = 1 ; for (int i = 2 ; i <= n; i++){ a[i] = 1LL *(a[i-1 ]+1 )*(a[i-1 ]+1 )%mod; dp[i] = 1 ; } int res = 0 ; for (int i = n-1 ; i >= 1 ; i--){ for (int j = i+1 ; j <= n; j++){ if (a[j] > a[i]){ dp[i] = max (dp[i], dp[j]+1 ); } } res = max (dp[i], res); } printf ("%d\n" ,res); } #ifdef CPC } #endif return 0 ; }
大规模
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <bits/stdc++.h> using namespace std;typedef long long LL;const LL maxn = 1000010 ;const LL mod = 1000000007 ;LL a[maxn]; int dp[maxn];#define CPC int main (void ) #ifdef CPC char bufin[40012 ],bufout[40012 ]; for (int t = 1 ; t <= 1 ; t++){ sprintf (bufin,"%02d.in" , t); sprintf (bufout,"%02d.out2" ,t); freopen (bufin,"rb" , stdin); freopen (bufout, "wb" , stdout); #endif LL n, b; while (~scanf ("%lld%lld" ,&n,&b)) { a[1 ] = b; dp[1 ] = mod; for (int i = 2 ; i <= n; i++){ a[i] = 1LL *(a[i-1 ]+1 )*(a[i-1 ]+1 )%mod; dp[i] = mod; } int k = 1 ; for (int i = 1 ; i <= n; i++){ if (dp[k] < a[i]) dp[++k] = a[i]; else { *lower_bound (dp+1 , dp+k, a[i]) = a[i]; } } printf ("%d\n" ,k); } #ifdef CPC } #endif return 0 ; }
待更参考:https://zhuanlan.zhihu.com/p/121032448
参考 《算法导论 (原书第三版)》 算法设计与分析|中国大学MOOC HDForum-动态规划|by杭电刘春英 图像压缩问题|博客园