图网络浅学：图神经网络及其发展 - GNN

前言

本文是一篇讲解图神经网络从原始的基础模型到各种推广和变体的总结性文章。首先模型是按照一定分类分章节的方式进行讲解的，其次也并没有严格按照模型提出的时间顺序进行编排。

由于图神经网络属于图深度学习，是对图嵌入等图浅层学习(传统图机器学习)方向的神经网络广延。为此，对于图的类型、相关的基础知识、常见的经典图嵌入算法模型，感兴趣还请观看本站对图嵌入的文章：

图嵌入：在图上的机器学习

https://qslie.top/posts/d5c25945

此外，本文前两个章节主要介绍的是图神经网络的任务驱动式由来，以及基础模型的核心数学原理，实在时间有限可以选择性跳过。

另一方面，本文章开头直接进行模型的讲解其实是与实际着手编程有不少违和的。读者可以先在【其他技术细节】一节中了解图学习的训练过程和一些进阶的预处理，然后再开始模型的学习。

图神经网络的开发库主要是Pytorch-Geometric，可以在下面的本站文章中了解更多。

PyG框架学习指南

https://qslie.top/posts/6c21563a

非欧氏空间

随着深度学习的发展，神经网络在计算机视觉和自然语言处理等领域都取得了很大的突破。但是在这些任务中，所处理的数据一般都是在欧几里得空间中表示的（如语音、图像、文本等都属于序列或者网格数据），但是在诸如物理系统建模、分子指纹学习、蛋白质作用位点预测等许多其他任务中，问我需要面临着处理非欧几里得结构的图（Graph）数据的问题。

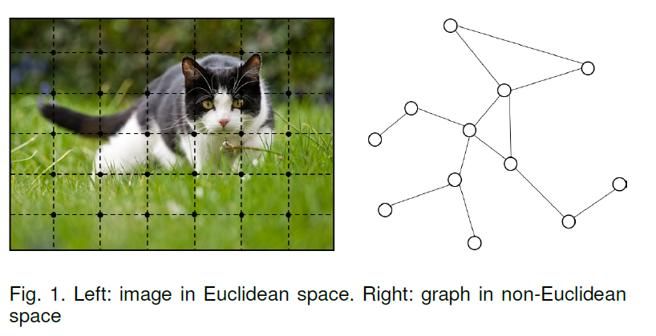
欧几里得空间

另一方面，现有的对上述两种常见数据类型进行处理的机器学习算法有一个核心假设：各个实例之间相互独立。这个假设也不再适用于图数据，因为每个实例（节点）都通过各种类型的连接（例如引用和交互）与其他实例相关联。

图结构数据的复杂性对现有的机器学习算法提出了重大挑战。近年来，出现了许多关于扩展图数据深度学习方法的研究。如今较为典型的图神经网络可以大致分为以下几类：

循环图神经网络
卷积图神经网络
图注意力神经网络（见：xxx待更）
图自监督学习模型（见：xxx待更）
时空图神经网络（见：xxx待更）

类比深度神经网络的其他方法，我们认为图结构的神经网络需要找到某种方法来“聚合”邻居节点的信息。

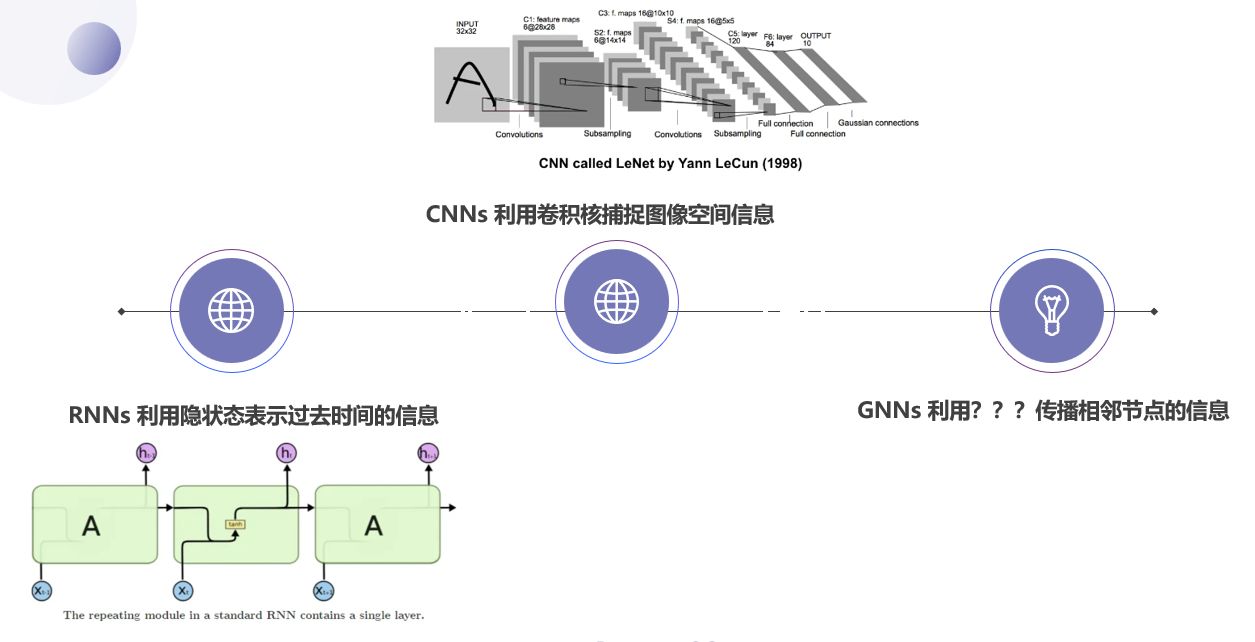
从以往的方法到图神经网络

巴拿赫不动点定理

图神经网络GNNs（Graph Neural Networks）最早是由 Marco Gori、Franco Scarselli 等人提出的。其核心思想是通过反复交换邻域信息来更新节点的状态，直到达到稳定的平衡。该思想源于不动点定理，具体来说是巴拿赫不动点定理。

在很多领域中，不动点是稳定和均衡的代表——博弈中的纳什均衡、阿罗-德布鲁经济体中的一般均衡和马尔可夫链的平稳分布都是不动点。不动点定理确立了具有特定性质的映射的不动点的存在性。

基本概念

【定义：不动点（Fixed Point）】设 $X$ 为非空集合， $T:X\to X$ 为一 $X$ 到自身的映射，若 $\exists x_0\in X,\;s.t.\; T(x_0)=x_0$ ，则称 $x_0$ 为映射 $T$ 的不动点。

【定义：利普希茨条件（Lipschitz Condition）】设 $(X,d)$ 为度量空间，即集合 $X$ 内的元素之间的“距离”可以由 $d$ 进行度量。设有映射 $T:X\to X$ ，若存在常数 $\alpha\in \mathbb R_+$ 使得对任意的 $x,y\in X$ 都有 $d(T(x),T(y))\leq \alpha\cdot d(x,y)$ ，则称 $\alpha$ 为利普希茨常数，该不等式为利普希茨条件，称 $T$ 为利普希茨连续映射。

一个函数（映射）利普希茨连续可推出该函数（映射）连续
此外，也有定义利普希茨常数是满足上式的最小的 $\alpha$ 值

【定义：压缩映射（Contraction Mapping）】设 $(X,d)$ 为度量空间，设有映射 $T:X\to X$ ，若存在常数 $0≤\alpha<1$ ，使得对任意的 $x,y\in X$ 都有 $d(T(x),T(y))\leq d(x,y)$ ，则称 $T$ 为压缩映射。

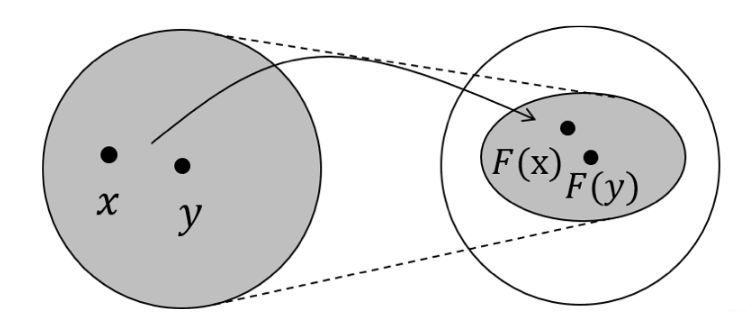
压缩映射示意图

字面意思理解的话，就是在映射之后两点的距离变短了(因为 $0\leq \alpha \lt 1$ )，也就是压缩了，如上图所示

【定义：收敛序列（Convergent Sequence）】设 $(X,d)$ 为度量空间，若数列 $\{a_n\}$ 满足 $a_i\in X,\;i=1,2,...,n$ ，且 $(\exists N\gt 0,L\in X),\;(\forall n \geq N),\;d(a_n,L)\lt\epsilon$ ，则称该数列为收敛列。

【定义：柯西序列（Cauchy sequence）】设 $(X,d)$ 为度量空间，若数列 $\{a_n\}$ 满足 $a_i\in X,\;i=1,2,...,n$ ，且 $(\exists N\gt 0),\;(\forall m,n \geq N),\;d(a_m,a_n)\lt\epsilon$ ，则称该数列为柯西列。

柯西列不一定是收敛列。如数列 $\{1/n\}\in X=(0,1)$ 是柯西列，但其收敛于0，而 $0\not\in X$ ，所以不是收敛列。

【定义：完备度量空间（Complete Metric Space）】若度量空间 $(X,d)$ 中的任意柯西序列都收敛，那么称 $(X,d)$ 为完备度量空间。

巴拿赫不动点

【引理】对度量空间 $(X,d)$ 和压缩映射 $T$ ，由 $x_1=a\in X,x_{n+1}=T(x_n),\;n\in\mathbb N$ 组成的序列为柯西列。且该序列收敛于压缩映射的不动点(记为 $x^*$ )。

基础图神经网络

对于给定带属性的加权图 $G=(V,E,X)$ ：
一个节点 $v\in V$ 通常由其本身的特征 $x_v\in X$ 和其相关的节点（通常是其相邻节点 $v'\in N(v)$ ）以及边上的权重 $x_e\in X,\;e=(v,v')\in E$ 共同表示。

GNN的目标就是在于为每个节点学习一个隐状态表示 $\mathbf h_v$ 来完全上述要求，即能编码该节点和其相邻节点的信息。利用状态表示可以获得模型的输出/嵌入表示 $\mathbf o_v$ .

状态表示

显然我们需要找到一种函数 $f$ 来将任意一个 $v$ 的邻点 $u\in N(v)$ 参与计算以得到隐状态表示 $\mathbf h_v$ 。于是有：

$\begin{aligned} \mathbf h_v&=\sum_{u\in N(v)}f(x_v,\;x_{(v,u)},\;\mathbf h_{u},\;x_u)\\ \mathbf o_v&=g(\mathbf h_v,\;x_v) \end{aligned}$

我们称 $f$ 为局部转移函数（local transition function）， $g$ 为局部输出函数。

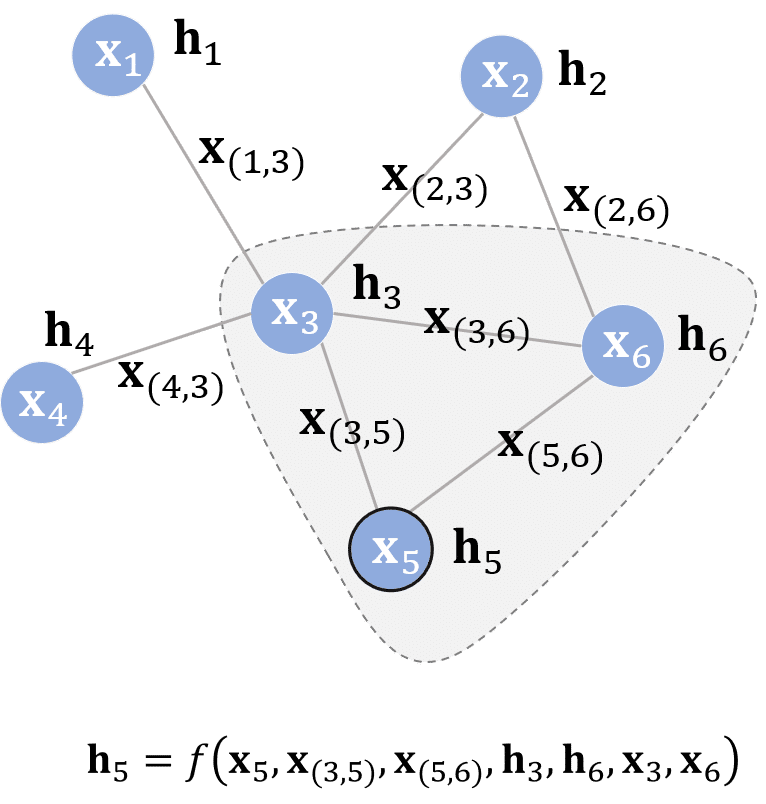
以上图为例，图中节点 $x_5$ 的隐状态如图所示。

如果将所有节点的结果都堆叠起来，用矩阵表示的话，隐状态矩阵可以写为：

$\begin{aligned} \mathbf H=F(\mathbf H,X) \end{aligned}$

其中， $\bf H$ 要求是函数的唯一的不动点，这就需要我们保证全局转移函数 $F$ 是一个压缩映射。

根据巴拿赫不动点定理，我们可以设定初始值 $\mathbf H^{(0)}$ ，然后不断迭代直到其数值变化趋于稳定。

$\begin{aligned} \mathbf H^{(t+1)}=F(\mathbf H^{(t)},X) \end{aligned}$

接下来问题就是如何设计函数 $F(\cdot)$ 使得它是一种压缩映射。

转移函数

事实上，对于转移函数，我们可以使用前馈神经网络（feedforward neural network，FNN）——多层感知机来实现。这也得益于其可以利用梯度下降法求解的便利性，以及在其他类型的深度学习任务中已经表现出的优秀性能。

如果考虑设计线性GNN，则全局转移函数可以设计如下：

$\begin{aligned} \text{let }\mathbf H&=[\mathbf{h}_1,\mathbf{h}_2,...,\mathbf{h}_n]^T\text{ then}\\ \mathbf h_i&=\sum_{j=1}^n\mathbf A_{i,j}\cdot\mathbf h_{j}+\mathbf b_{i}=\mathbf A_{i,:}·\mathbf H+\mathbf b_i\\\\ F&=\mathbf {AH+b} \end{aligned}$

其中， $\bf A$ 是分块矩阵，每一个分块 $\mathbf A_{i,j}$ 是由节点 $i$ 的特征、其邻点 $j$ 的特征以及它们的边权（边特征）reshape 得来（如果未相邻则边特征置零）。
具体来说，事先通过一个前馈神经网络的映射 $\phi:\mathbb R^{2|V|+|E|}\to\mathbb R^{s^2}$ 将 $[x_i,\;x_{(i,j)},\;x_j]$ 重排为 $s\times s$ 的矩阵 $\bf B$ （假设隐状态 $\mathbf h_j$ 的维度是 $s$ ），于是对其进行缩放：

$\mathbf A_{i,j}=\frac{\mu}{s\times |N(j)|}\bf B$

其中， $\mu\in(0,1)$ 为缩放因子。（事实上偏置 $\bf b_j$ 也需要缩放为 $s$ 维，方法类似，此处不赘述）

最终我们的目标就是在迭代中不断更新隐藏状态表示 $\bf H$ ，该过程同样可以利用深度学习中反向传播和梯度下降的思路。

此外，根据压缩映射的充分条件，我们要求 $F$ 的雅可比矩阵的范数小于1，而考虑线性网络时，我们容易得出：

$\begin{aligned} \frac{\partial F}{\partial\mathbf H}&=\bf A\\ ||\mathbf A||&=\frac{\mu}{s\times |N(j)|}||\mathbf B||\leq\mu\lt1 \end{aligned}$

因此，用前馈神经网络作为压缩映射时，符合条件。

另外，对于非线性网络，我们希望雅可比矩阵的范数小于 $c,\;c\in(0,1)$ （可调参数），那么可以通过在训练时给损失函数额外添加惩罚实现：

$J=Loss+\lambda\cdot\max\left(0,\left|\left|\frac{\partial F}{\partial\mathbf H}\right|\right|-c\right)$

怎么判断一个映射是不是压缩映射? - 知乎

网络结构

通过以上描述，我们可以将一个简单的图神经网络的过程用下图表示。

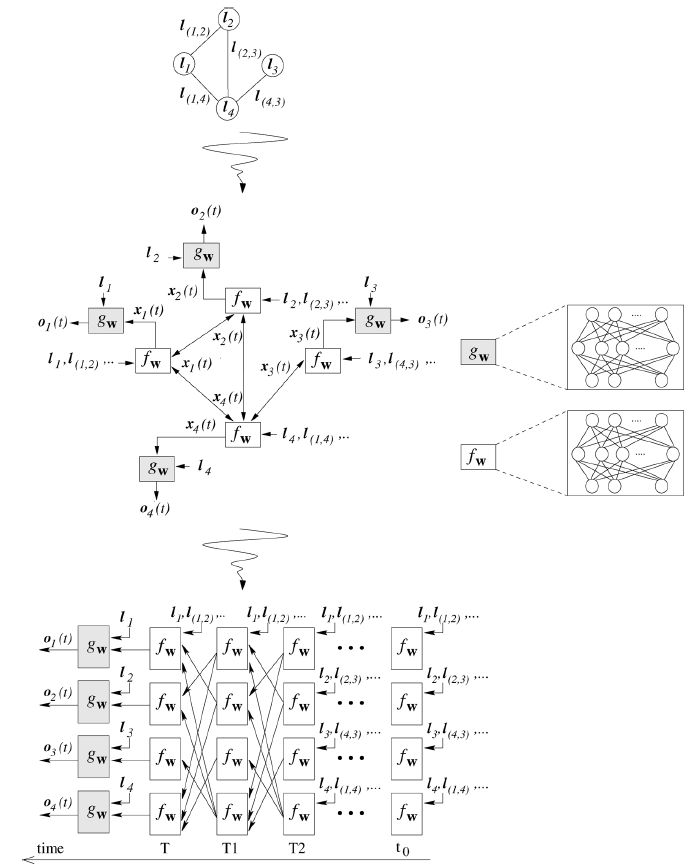
图神经网络架构

注：因为历史和习惯等原因，原始论文 《The graph neural network model》 所用的符号与本文有所不同。
上图中的 $\boldsymbol l_i$ 代表的是节点 $i$ 的 label，其实也就是我们今天所说的节点特征向量 $x_i$ ，边特征向量同理.

参数学习过程

整个参数的学习主要分为两个部分，前向传播和后向传播。

前向传播

输入：给定隐状态迭代停止条件 $\epsilon_f$ 、当前参数 $\bf W$ 和确定的图 $G$ ；
输出：不动点 $\bf H$

传播过程大致总结如下：

初始化各个隐状态 ${\bf h}^{(0)}_i$
循环迭代，根据转移函数 $F$ 更新隐藏状态 $\mathbf H^{(t+1)}=\sigma(\mathbf A\mathbf H^{(t)}+\mathbf b)$ ，激活函数 $\sigma(·)$
计算是否满足停止条件： $||\mathbf H^{(t+1)}-\mathbf H^{(t)}||\leq\epsilon_f$
迭代步 $t$ 自增
循环结束得到表示 $\bf H$ .

实际上编码网络（网络结构图的中间部分）仅仅类似于静态的前馈神经网络，但是对 $\bf H$ 的迭代过程相当于不断经过一层又一层神经网络，因为结束条件是隐状态的稳定，所以这个层数是动态确定的，并且网络权重根据输入图的拓扑结构来共享。所以为静态网络设计的二阶学习算法、剪枝算法、以及逐层学习算法无法直接应用于 GNN 。

后向传播

模型中需要学习的参数是将各特征进行reshape 的神经网络映射 $\phi$ ，具有参数 $\bf W$ 。
于是通过链式法则从迭代步 $t=T\to0$ 逐步往前追溯（相当于从最后一层网络往前传播，但是权重是共享的），用于计算 $\frac{\partial J}{\partial\mathbf W}$ ，然后通过梯度下降法更新权重。

该过程由于使用了梯度下降法，所以也需要一个收敛的结束条件（注意与隐状态结束条件不同！）

基础GNN的不足

实验结果表明GNN对于结构化数据的建模十分有效，但仍然存在着诸多的不足：

对于不动点隐藏状态 $\bf H$ 的更新十分低效；
GNN在迭代的过程中用共享参数 $\bf W$ ，然而大多标准网络在不同的网络层数使用不同的参数；
在原始的GNN中难以有效建模的带边标签的特征。例如，在知识图谱中边代表着节点间的关系类型，不同边的消息传递应该根据他们的类型有所不同。怎么样去学习边的隐藏状态也是—个重要的问题；

频域图卷积网络

卷积神经网络的出色表现让我们“急不可耐”地想将其推广到图神经网络中，我们希望它在图里能够改善基础GNN的不足。

而卷积这一概念，追根溯源就和《信号分析与处理》脱不了干系了。事实上谈到卷积我们应该有共识，那就是在频域上的卷积和时域上的卷积（图像处理领域我们把后者称作空域，图论中也是类似的说法）。卷积的进一步联系是傅里叶变换，它为我们提供了不同频率的正弦波和余弦波的特定基 (DFT 矩阵，例如 Python 中的 scip.linalg.dft)，这样我们就可以将信号或是图像表示为这些波的总和。

所以，显而易见地，对于图卷积同样也分了两个域来研究：频域和空域。很多时候，图的频域我们也叫图的谱域（图谱）。

在图论中，“频谱” 意味着拉普拉斯矩阵 $L$ 的特征分解。可以认为拉普拉斯矩阵 $L$ 是一种特殊的邻接矩阵，而特征分解就是为了找到构成我们的图基本正交分量的一种方法。

关于拉普拉斯矩阵和图傅里叶变换的内容，本站其他文章做了更详细的介绍和推导，本文默认读者已经了解。

图论：从拉普拉斯算子到拉普拉斯矩阵

https://qslie.top/posts/7cec7657

切比雪夫最佳逼近

图卷积在谱域上的定义由下式给出。而 $f,U,\varLambda$ 均由我们给出的图 $G$ 唯一确定。所以对于深度学习任务，我们需要学习的是参与卷积的 $g$ 。

$f*g=Ug_\theta(\varLambda) U^Tf$

得益于图谱卷积相当于是做矩阵乘法，所以计算机只需学习对角矩阵 $g_\theta(\varLambda)$ 即可（ $\varLambda$ 是拉普拉斯矩阵做特征分解得到的特征值对角矩阵）。

显然，当图节点数量 $n$ 足够大时，计算机对图卷积的计算代价将会很大程度地增加，所以必须进一步考虑计算优化的问题。
在论文《Wavelets on Graphs via Spectral Graph Theory》中，作者给出的方法是利用切比雪夫最佳逼近多项式。

相关知识可参阅：初识切比雪夫多项式 - 知乎

任意一个连续函数 $f(x),\;x\in[-1,1]$ 都可以被展开为切比雪夫多项式级数：

$\begin{aligned} f(x)&=\sum_{n=0}^\infty A_nT_n(x)\\ \text{where }A_0&=\frac1\pi\int_{-1}^1\frac{f(x)}{\sqrt{1-x^2}}\mathrm dx\\ A_n&=\frac2\pi\int_{-1}^1\frac{f(x)T_n(x)}{\sqrt{1-x^2}}\mathrm dx \end{aligned}$

其中， $T_n(x)$ 为 $n$ 次切比雪夫多项式，其递推式为：

$T_0(x)=1,\;T_1(x)=x,\;T_{n+1}(x)=2xT_n(x)-T_{n-1}(x)$

我们的目标就是将切比雪夫多项式级数的前 $K$ 项近似替代 $g_\theta(\varLambda)$ 。为此，我们需要对特征值（函数 $g_\theta$ 的自变量）进行拉伸或收缩，使得 $\lambda_i\in[-1,1]$ . 方法也非常简单：

$\tilde{\varLambda}=\frac2{\lambda_{\max}}\varLambda-I$

从而我们有：

$g_\theta(\varLambda)\approx\sum_{k=0}^K\theta_k'T_k(\tilde{\varLambda})$

其中 $\theta'\in\Bbb R^{K+1}$ 为切比雪夫系数。

接下来再带入到卷积公式：

$\begin{aligned} f*g&\approx U\left(\sum_{k=0}^K\theta_k'T_k(\tilde{\varLambda})\right)U^Tf \\&=\sum_{k=0}^K\theta_k'UT_k(\tilde{\varLambda})U^Tf \\&=\sum_{k=0}^K\theta_k'T_k(U\tilde{\varLambda}U^T)f \\&=\sum_{k=0}^K\theta_k'T_k(\tilde{L})f\qquad\text{//}\because L=U\varLambda U^T \end{aligned}$

其中，我们的 $\tilde{L}$ 需要 $\lambda_{\max}$ 作为前置知识，但是根据拉普拉斯矩阵的对称归一化 $L_{sym}$ 的基本性质，其瑞利商最大值为2（也就是说 \lambda_\max=2），因此我们只需对 $L$ 进行归一化之后，得到：

\tilde{L}=\frac2{\lambda_\max}L-I=L-I

最终，计算机实际上只需要学习的是系数 $\theta'_k,\;k=0,1,...,K$ 。

可见，最终的近似表达式不再需要 $U,\varLambda$ 的参与了，换句话说就是无需再对拉普拉斯矩阵做特征值分解了。而特征值分解正是计算代价巨大的原因。
其次，因为切比雪夫多项式的递归性质，在计算上每次只需要根据前两次的结果做乘法和减法，就可以得到当前结果。

SpectralNet

Spectral Convolutional Neural Network (SCNN) 谱卷积神经网络 是由 Joan Bruna 等人于2014年提出的。
类似于卷积神经网络，SCNN 在归一化的拉普拉斯矩阵谱域上定义图卷积操作，其中待学习的参数就是每一层的卷积核 $\Theta:=g_\theta(\varLambda)$ 。

具体来说，第 $k$ 层网络的第 $j$ 个通道，其所有节点的输出特征堆叠 $\mathbf H^{(k)}_{:,j}$ 就可以表示为：

$\mathbf H^{(k)}_{:,j}=\sigma\left(\sum_{i=1}^{c_{k-1}}U\Theta_{i,j}U^T\mathbf H^{(k-1)}_{:,i}\right)$

即 $k-1$ 层的 $c_{k-1}$ 个通道都与对应的卷积核进行卷积，最后相加起来并经过激活函数。

显然 Spectral CNN 面临三个问题：

对图的任何扰动都会导致特征基的变化；
学习到的卷积核是邻域相关的，因此不能应用于具有不同结构的图；
特征分解需要 $O(n^3)$ 的计算复杂度（Spectral CNN 并没有做近似处理）

ChebNet

Chebyshev Spectral CNN (ChebNet) 切比雪夫卷积神经网络 由 Michael Defferrard 等人在2016年提出。正如它的名字一样，ChebNet 利用了切比雪夫多项式的最佳逼近多项式方法，简化了卷积的计算。

其中，

卷积核只有 $K+1$ 个可学习的参数，大大降低了参数的复杂度
ChebNet 不需要对拉普拉斯矩阵做特征分解了，这是区别于SCNN的非常明显的一点，它省略了最耗时的步骤
ChebNet 的卷积核具有空间局部性， $K$ 正好是卷积核的“感受野半径”，即将中心顶点的 $K$ 阶邻点作为邻域节点

GCN | GraphConvNet

Graph Convolutional Network (GCN) 图卷积网络 在2017年由 Thomas Kipf 和 Max Welling 提出。他们在 ChebNet 的基础上限制 $K=1$ ，并取 \lambda_\max=2（正如我们之前推导的那样），这缓解了节点度分布范围较大时产生的局部结构过拟合问题。

不难得出卷积操作被简化如下：

$f*g\approx\theta_0'f+\theta_1'\tilde{L}f$

为了限制参数的数量并避免过拟合，GCN 进一步假设 $\theta=\theta_0'=-\theta_1'$ .
代入 $\tilde{L}=L_{sym}-I=-D^{-1/2}WD^{-1/2}$ ，最终可得：

$f*g\approx\theta\left(I+D^{-\frac12}WD^{\frac12}\right)f$

值得注意的是，叠加很多个卷积层的时候，可能会出现数值不稳定以及梯度爆炸/消失的情况，所以论文中引入了一个重归一化的技巧 (renormalization)：

$\begin{aligned} A&:=W\qquad\text{//论文中将$A$记为邻接矩阵(可带权)}\\ \text{let }\tilde{A}&=A+I\\ [\tilde{D}]_{ii}&=\sum_{j=1}^nA_{ij}\\ f*g&:=\theta\left(\tilde D^{-\frac12}\tilde A\tilde D^{\frac12}\right)f \end{aligned}$

最终，具有 $C$ 个通道的图，每个节点的特征堆叠得到的输入信号 $\mathbf X\in\Bbb R^{n\times C}$ 经过 $F$ 个（输出通道数）卷积核之后得到的输出信号 $\mathbf Z\in\Bbb R^{n\times F}$ 如下：

$\mathbf Z=\sigma\left(\tilde D^{-\frac12}\tilde A\tilde D^{\frac12}\bf X\Theta\right)$

这里说的通道数 $C,F$ 其实也可以理解为输入特征的维度和输出特征的维度。通道数是沿用图像卷积的说法。

GCN的网络结构图

值得注意的是，如果我们再把 $\tilde D^{-\frac12}\tilde A\tilde D^{\frac12}$ 记作 $\hat{A}$ ，将其视为一种归一化后的邻接矩阵。那么 GCN 输出信号的 $\hat{A}X\Theta$ 就可以看作通过邻接矩阵对每个节点的邻点做某种加权平均。这与空间域图卷积的思想一致。所以 GCN 除了频域上的卷积解释外，也有空域中的解释。

🧬GCN官方网站：https://tkipf.github.io/graph-convolutional-networks

AGCN | 自适应图卷积

上述模型均使用原始的图结构来表示节点之间的关系。然而不同节点之间也可能存在隐式关系。简单来说就是，可能邻居节点的相似性比非邻居节点还要更低，这是因为在一定情况下固定的图的结构的并不代表节点相邻特征相似。

于是 Adaptive Graph Convolutional Network (AGCN) 自适应图卷积网络 被提了出来，它通过学习“残差”拉普拉斯矩阵 $L_{res}$ 与原来的 $L$ 结合来学习这种隐式关系，模型/论文中的 SGC-LL Layer 就是在做这个事。

因为拉普拉斯矩阵代表了图的拓扑结构，而如果将节点间新的关系添加进去将会得到包含隐性相关性的新拓扑。作者利用广义的马氏距离（mahalanobis distance）计算节点间的距离：

$D(x_i,x_j)=\sqrt{(x_i-x_j)^T\boldsymbol M(x_i-x_j)}$

狭义的马氏距离中， $\boldsymbol M$ 为数据的协方差矩阵；此外，当它是单位阵时，就变成了欧氏距离

在 AGCN 模型中 $\boldsymbol M$ 是对称的半正定矩阵，保证 $\boldsymbol M=W_dW_d^T$ 且 $W_d∈\Bbb R^{d \times d}$ 是用于学习的权重参数， $d$ 为节点特征维度。基于马氏距离得到高斯核计算公式如下：

$\Bbb G_{x_i,x_j}=\exp(-D(x_i,x_j)/(2\sigma^2))$

对其进行标准化后得到密集的邻接矩阵 $\hat{A}$ ，残差矩阵就为 $L_{res}=I-\hat D^{-1/2}\hat{A}\hat D^{-1/2}$ ，其中的 $\hat D$ 也是由 $\hat{A}$ 中的度得来的。

于是，新的拉普拉斯矩阵就被定义为 $\hat L=L+\alpha L_{res}$ ， $\alpha$ 为可调超参数。

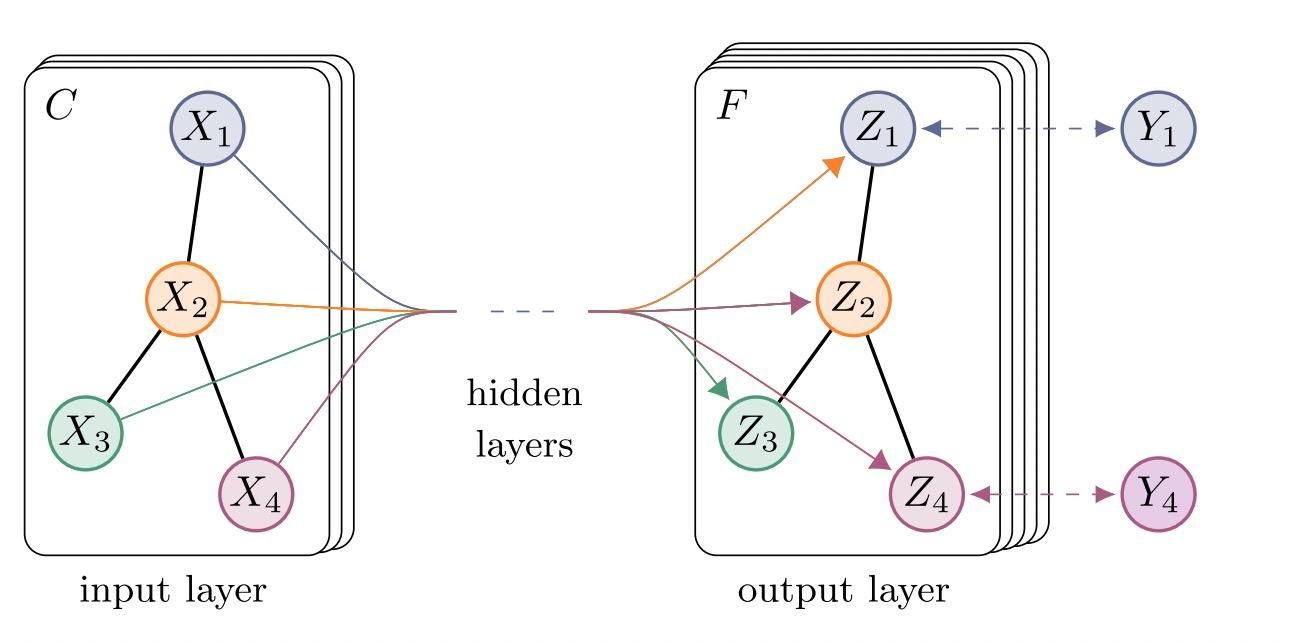
DGCN | 对偶图卷积

Dual Graph Convolutional Network (DGCN) 对偶图卷积网络 同时考虑了图的局部一致性和全局一致性——利用两个共享权重的卷积网络进行捕捉。该工作还采用了无监督损失函数在最后对二者进行聚合。

Note: 对偶翻译自 dual，代表论文中提到的两个卷积网络。而有些情况，谈到 对偶图 则指的是“将边转换为顶点、将顶点转换为边”的新图 $G'$ 与原来的图 $G$ 之间是对偶关系。

用于捕捉局部一致性的卷积网络 $\text{Conv}_A$ 与 GCN 模型一致；
用于捕捉全局一致性的卷积网络 $\text{Conv}_P$ 利用正点互信息矩阵 PPMI 代替邻接矩阵。

$\mathbf H’=\sigma\left(\mathbf{D}_p^{-\frac12}{\bf X}_p\mathbf{D}_p^{-\frac12}{\bf H\Theta}\right)$

其中， ${\bf X}_p$ 为PPMI矩阵， ${\bf D}_p$ 是 ${\bf X}_p$ 的对角度矩阵。

空域图卷积网络

与图像中的卷积神经网络类似，基于空间的图卷积将中心节点的表示与其相邻节点的表示进行卷积，以得出中心节点的更新表示。具体可参考下图。

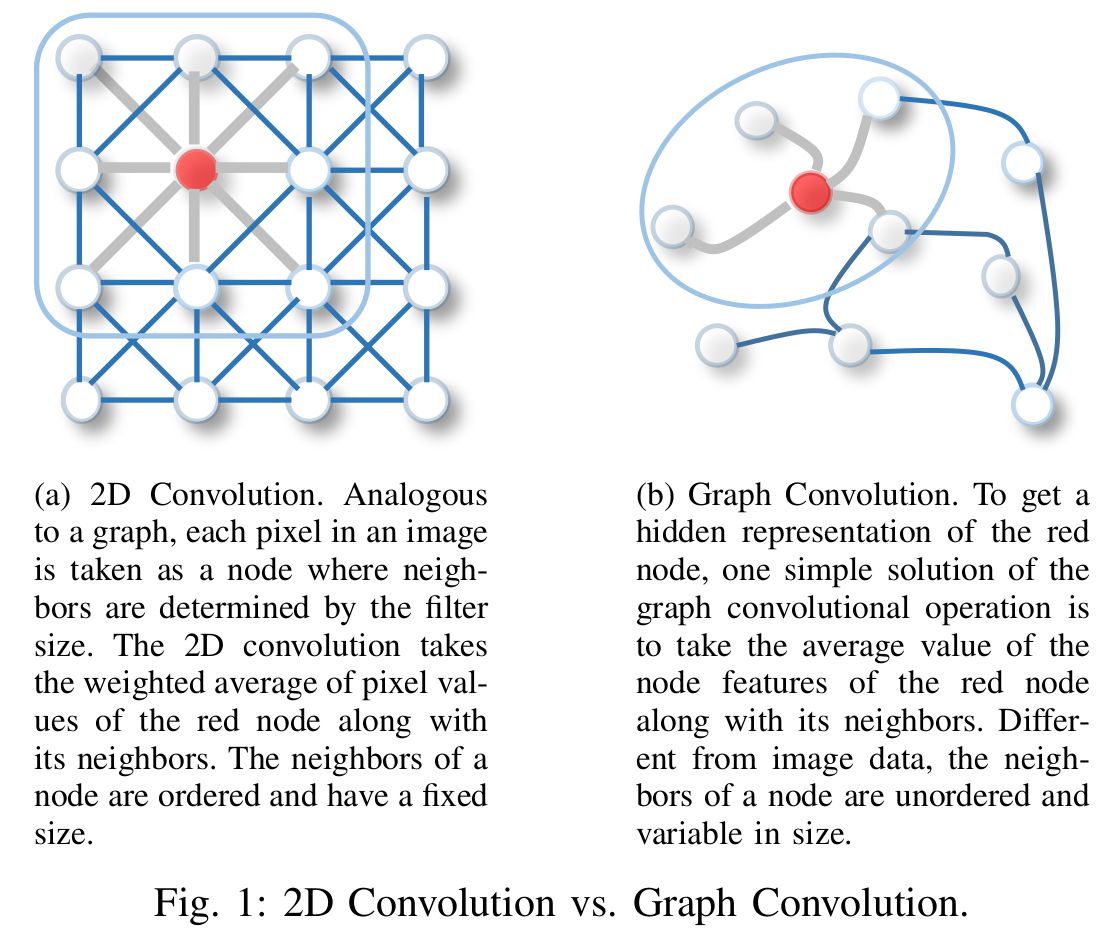
2D-Conv 和 Graph-Conv

从另一个角度来看，基于空间的 ConvGNN 其实是和我们最早提出的 基础GNN 中，共享信息传播/消息传递的思想，是一样的。其实空间图卷积操作本质上就是沿边传播节点信息。

MPNN | 消息传递网络

Message Passing Neural Network (MPNN) 消息传递神经网络 是由 Google 科学家提出的一种图监督学习模型。这个模型比我们下面将要介绍的模型提出得较晚，但是因为其概括性好的，为了方便理解我们先讲解它。

严格意义上讲，MPNN不是一种具体的模型，而是一种空域卷积的形式化框架和范式。它将空域卷积分解为两个过程：消息传递与状态更新操作。分别由函数 $M(·),U(·)$ 完成。MPNN在卷积层结束之后，针对各节点的信息利用读出函数 $R(·)$ 计算整个图的特征向量。

消息传递阶段：节点 $v$ 在第 $l+1$ 层的隐状态可以用下面这个表达式得出：

$\mathbf{h}_{v}^{(l+1)}=U_{l+1}\left(\mathbf{h}_v,\sum_{u{\in}N(v)}M_{l+1}(\mathbf{h}_u^{(l)},\mathbf{h}_v^{(l)},\mathbf{x}_{(v,u)})\right)$

读出阶段：根据整个图的特征（Graph Feature），将其映射为一个描述全图特征的特征向量（Eigenvector）：

$\hat{y}=R\left(\{\mathbf h^{(K)}_v\mid v\in G\}\right)$

其中， $K$ 为最终卷积层的层数。

MPNN看起来与基础的GNN模型十分相似，但是它并没有基于巴拿赫不动点定理来更新状态的。我们选取的层数 $K$ 决定了聚合多少步长的邻点的信息。这就是图卷积网络中常提到的 $K\text{-}hop$ 。一个简单的 $K\text{-}hop$ 即图卷积过程如下图所示：

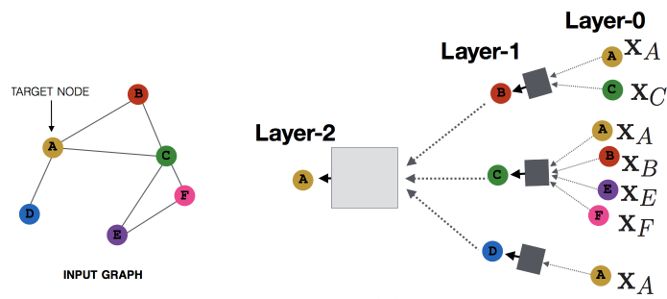
MPNN的图卷积

简单起见，我们仅仅看 $K=2$ 时的信息传递过程，并且为了方便展示，只聚焦于单个目标节点的更新。

设目标节点为 $A$ ，与之相邻的节点就是 $B,C,D$ 。那么，它们的信息聚合给 $A$ 将是最后一层所做的事。同理，与 $A$ 的距离是 2 的那些节点会在倒数第二层聚合到 $B,C,D$ 中，以此类推。

当我们选取不同的函数来进行信息传递、状态更新和全局信息读出时，就可以演化出不同的空域卷积的图神经网络。

Neural FP

2015年，David Duvenaud 等人在论文《Convolutional Networks on Graphs for Learning Molecular Fingerprints》中提出了针对具有不同度的节点使用不同的权重矩阵，并以此得到了模型 Neural FP。

该模型十分简洁，通过聚合节点 $v$ 的邻点表示，并且和自身的嵌入表示相加，然后由权重矩阵进行转换就能得到本层的嵌入表示输出。

$\mathbf h_v^{(k)}=\sigma(\mathbf xW_k^{|N(v)|})$

其中， $\mathbf x=\mathbf h_v^{(k-1)}+\sum_{u\in N(v)}\mathbf h_u^{(k-1)}$ ， $W^t$ 表示节点度为 $t$ 时所使用的权重矩阵。

事实上这个模型就是将MPNN的信息传递函数设置为去除了偏置的仿射变换，增加了权重矩阵的类型。

然而，因为 Neural FP 存在处理大规模图导致参数量过大的情况，所以并不能很好地适用于其他任务。

PATCHY-SAN

此前我们的学习都是想办法基于图结构这种非欧式结构的数据进行神经网络的衍生。而2016年的《Learning Convolutional Neural Networks for Graphs》则另辟蹊径：通过将图结构抽离并表示出来，然后在经典的CNN模型上训练。

原论文的地址：https://arxiv.org/pdf/1605.05273v2.pdf；
官方PPT讲解：https://www.matlog.net/icml2016_slides.pdf

这项工作主要分为四个步骤：

选择 $w$ 个节点序列；
从所选择的每个节点中根据图结构衍生出包含该节点的连通子图，节点数为 $k$ ， $k$ 也是感受野；
图归一化：为 $w$ 个子图映射出序号，序号从 $1\to k$ ；
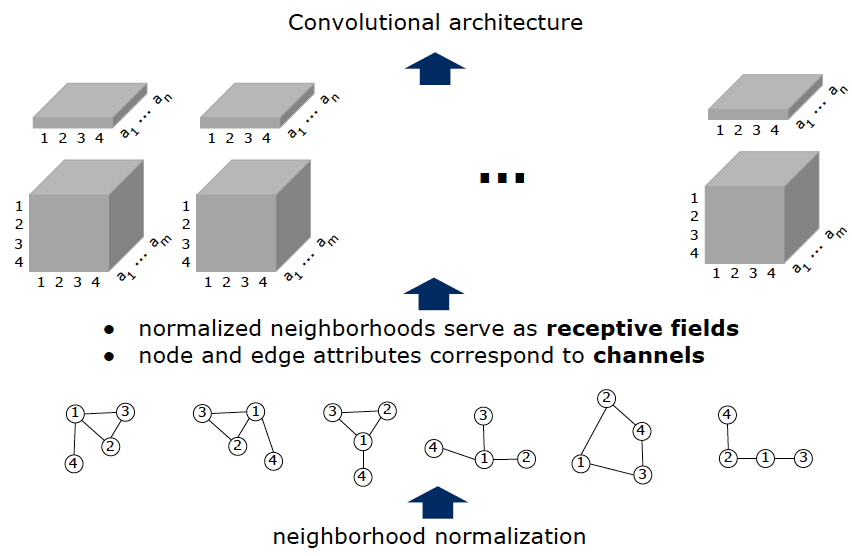
提取特征：将子图节点的节点特征与边特征作为传统CNN的通道建立新的欧式空间数据；

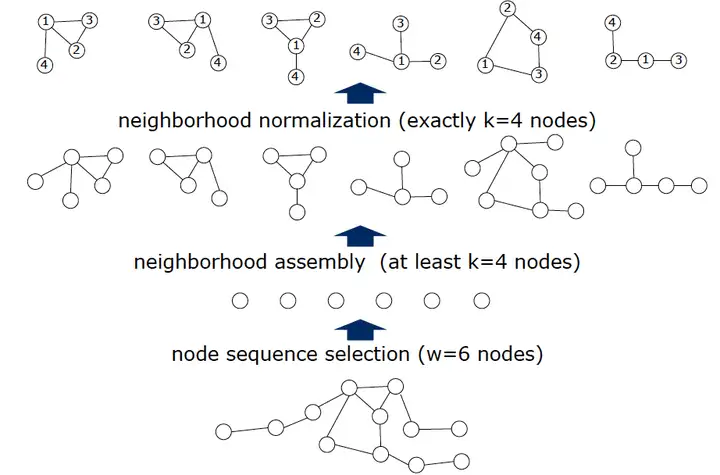
PATCHY-SAN特征提取

最后，将提取出来的数据输入到传统CNN模型中进行训练。

PATCHY-SAN训练

NN4G

Neural Network for Graphs (NN4G)是第一个提出的基于空间的ConvGNNs。

NN4G通过直接累加节点的邻域信息来实现图的卷积，此外它还吸收了残差网络的跳接来记忆每一层的信息（累加此前每一层的特征）。

$\mathbf H^{(k)}=\sigma\left(\mathbf{XW}^{(k)}+\sum_{i=1}^{k}A{\bf H}^{(i-1)}\Theta^{(i)}\right)$

不难发现，NN4G的主体部分—— $AH\Theta$ 是和 GCN 一样的，只是 $A$ 并不是用了经过归一化的 $\tilde{A}$ ，这可能会导致隐藏节点状态具有极其不同的尺度。

DCNN | 扩散卷积

Diffusion Convolutional Neural Network (DCNN) 扩散卷积神经网络 将图卷积视为扩散过程。它假设信息以一定的转移概率从一个节点转移到其相邻节点之一，使得信息分布在几轮后达到平衡。

事实上，这个过程与马尔科夫链的随机游走过程一致。所以可以自然而然地得出第 $k$ 层（也就是传播/扩散到了步长为 $k$ 的顶点）时，各个顶点的隐藏表示矩阵：

$\mathbf H^{(k)}=\sigma\left(\mathbf{W}^{(k)}\odot\mathbf{P}^k\mathbf{X}\right)$

其中，概率转移矩阵由 $\mathbf{P=D^{-1}A}$ 计算得出。

DCNN 将每一层的隐藏表示矩阵全部连接在一起作为最终的输出。使用概率转移矩阵的幂意味着遥远的邻居向中心节点贡献的信息非常少。

关于随机游走与马尔可夫模型可参考本站文章：

马尔可夫的计算美学

https://qslie.top/posts/25eb9964

其他技术细节

数据集划分

图神经网络的训练和其他结构的网络一样，可以分为基于有监督的标签训练及无监督的训练。但其中，特别是针对有监督学习而言，最让新手产生疑惑的点就是，这种图结构的输入数据集应该怎么划分成对应的训练集、验证集和测试集。

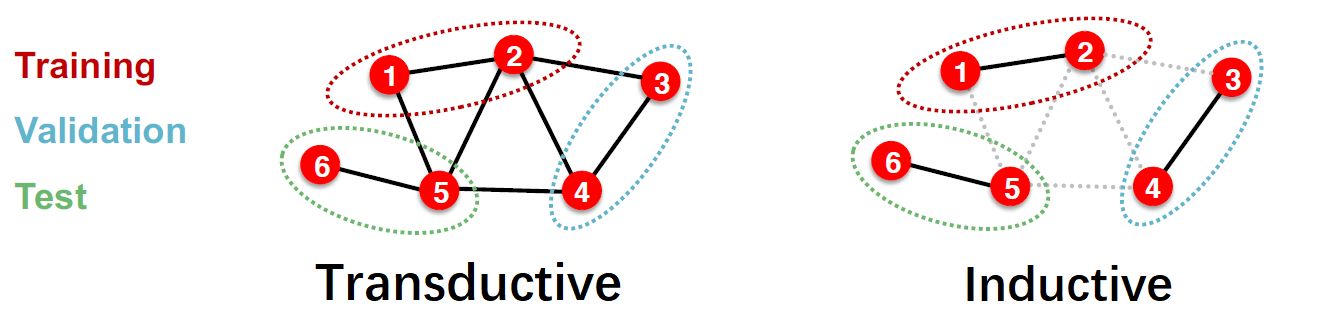
事实上这个问题如图所示，更进一步地分化出了两种学习任务或设置：

Inductive Setting（归纳式学习）：数据集本身构成了一个完整的图，训练阶段将此图分离出多个子图，从一系列子图里按比例划分训练集、验证集和测试集。通常训练阶段只是在子图上进行，而在测试阶段则需要用学习到的网络来预测训练时完全没接触过的未知点（unseen node）。如果数据集是一系列图的集合（或动态图），则是以一张张图为单位进行数据划分。由于这个特性，归纳式学习是可以迁移的。即在这个图上训练好的模型，可以迁移到另外一个图中使用，与传统的其他深度学习任务相同。
Transductive Setting（直推式学习）：数据集本身构成了一个完整的图，但是训练时用到了整张图的结构信息，只对按比例划分出来的节点或边提供 ground truth 用作训练，其余的节点或边的标签在训练时不可见，只在训练好后用作验证或测试。显然由于这个特性，这类学习方法不适用于 graph-level 任务。BTW，这种学习某种程度上也是半监督学习（semi-supervised learning）。

GCNs论文的作者采用的就是 Transductive Learning，而接下来我们将介绍的 GraphSAGE 论文则是一种 Inductive Learning 方法。

采样与聚合 | GraphSAGE

由于实际工程中节点的邻居数量可能从一到一千甚至更多不等，因此获取节点邻居的全部大小是低效的。

2017年由 William Hamilton 等人提出的 GraphSAGE 作为一个通用的归纳推理模型（Inductive learning），利用了采样方法为每个节点获取固定数量的邻居，然后再通过聚合得到所有邻居节点的单一表示。整体流程如下：

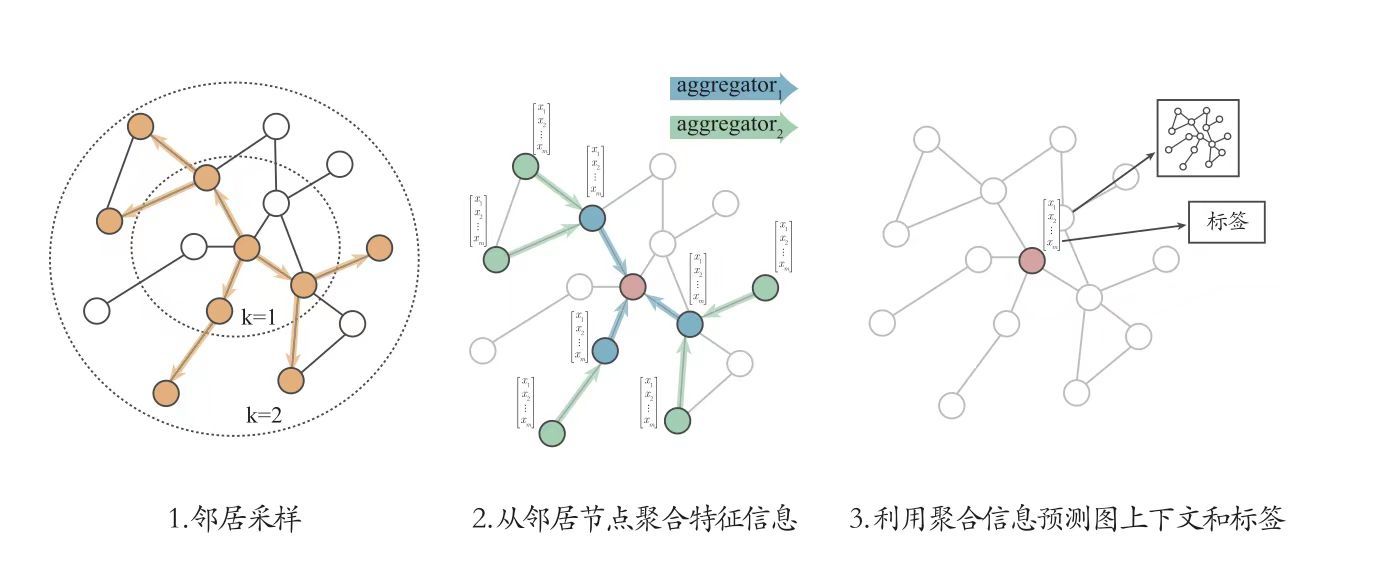
GraphSAGE

具体来说，GraphSAGE中的过程主要分为以下两点：

在图中随机采样若干个节点（要更新的目标节点集合），节点数为传统任务中的batch_size。对于每个节点，随机选择固定数目的邻居节点 (这里邻居不一定是一阶邻居，也可以是二阶邻居) 构成用于卷积操作的子图。
将邻居节点的信息通过 $\rm Aggregator$ 函数聚合起来，然后更新刚才采样的目标节点。

最终得出，GraphSAGE的状态更新公式如下：

$\mathbf{h}_{v}^{(l+1)}=\sigma\left(\mathbf{W}^{(l+1)}\cdot \text{Aggregator}(\mathbf{h}_v^{(l)},\{\mathbf{h}_u^{(l)}\mid{\forall}u{\in}N(v)\})\right)\;$

事实上，GraphSAGE最核心的贡献就是提出了采样的思想。而这里的聚合与MPNN范式以及GCN的"信息传递与更新"的思想是类似的。不过，GraphSAGE也给出了不同的聚合器方法以供参考：

Mean Aggregator：直接取邻居节点的平均
GCN Aggregator：将邻居节点与目标节点算在一起共同进行平均（物理意义正好和GCN相同，因而这样取名）
LSTM Aggregator：使用LSTM来 encode 邻居的特征。这里忽略掉邻居之间的顺序，即随机打乱，作者的想法是LSTM的表示能力比较强。但因为LSTM是处理序列数据的，因此不同打乱顺序会得出不同的结果
Pooling Aggregator：把各个邻居节点单独经过一个MLP得到一个向量，最后把所有邻居的向量做一个element-wise 的 max-pooling或者其他的pooling。公式如下：

$\text{Aggregator}_k^{\rm pool}=\max_{u\in N(v)}\sigma(W_{\rm pool}\mathbf h_u^{(k)}+b)$

一个利用池化聚合器编码邻居节点的嵌入表示/特征/隐状态，并且使用拼接的方式结合样本目标节点的特征和邻居节点的特征，最终用于有监督学习的 GraphSAGE 流程可以用下图进行直观地展示：

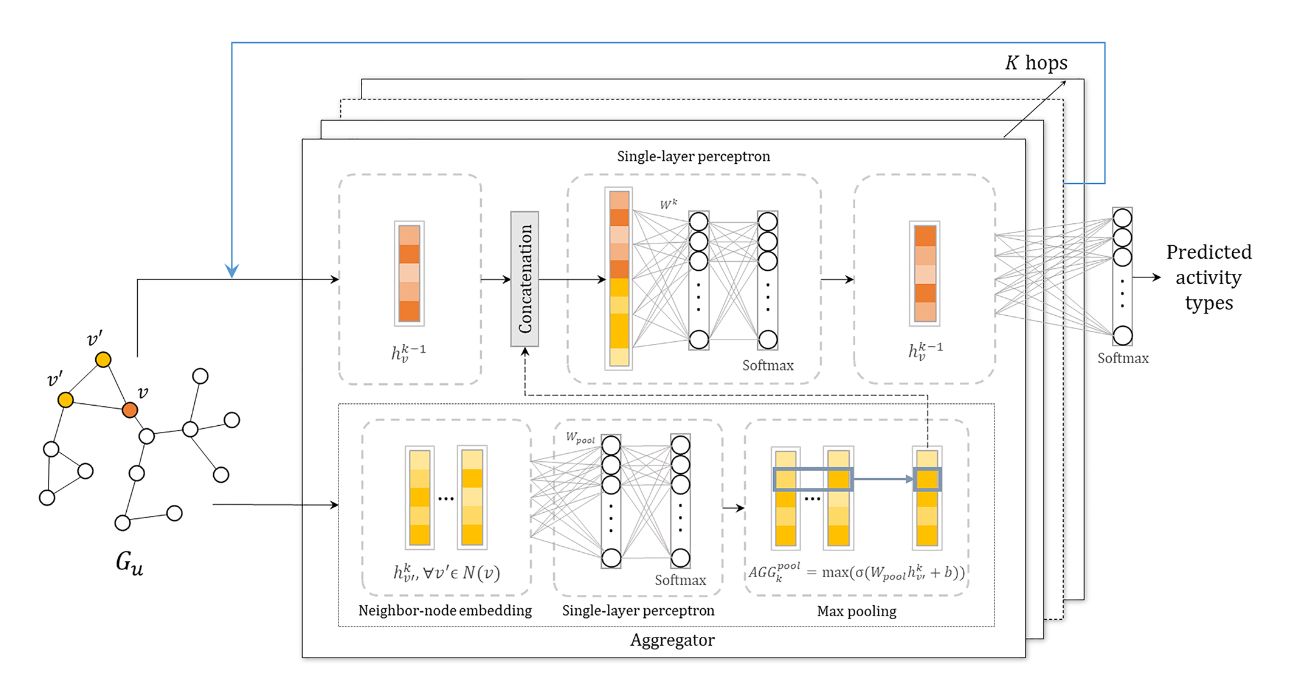
监督学习与聚合器的结构

图片摘自：《Graph-based representation for identifying individual travel activities with spatiotemporal trajectories and POI data》

层级池化

待更：图粗化、可微池化

图注意力网络(GAT)

原始论文：https://arxiv.org/abs/1710.10903
Github：https://github.com/Diego999/pyGAT

GCN的局限性

无法完成归纳（inductive）任务，也即处理动态图问题；
处理有向图的瓶颈，不容易实现分配不同的学习权重给不同的 neighbor；
对于一个图结构训练好的模型，不能运用于另一个图结构（所以此文称自己为半监督的方法）；

为了解决以上问题，已经在序列任务中表现出强大能力的注意力机制被提出用于 GCNs 的“传递邻居消息”的过程中。所以，图注意力网络（Graph Attention Networks，GAT） 其实是图卷积网络家族的一种方法。

如果你尚不了解注意力机制，那么本站也有对注意力机制的相关介绍：

Attention！注意力机制

https://qslie.top/posts/e00c7064

图注意力层

对于含有 $N$ 个节点的图，我们一共会构造 $N$ 个图注意力网络，因为每一个节点都需要对于其邻域节点训练相应的注意力。而图注意力网络的层数 $K$ ，也就是选择使用多头注意力机制，则根据需要决定。

我们在这里先分析 $K=1$ ，即一个单层图注意力网络的工作原理。我们给出两个相邻节点 $i,j$ 的评分函数 $e_{ij}$ 和权重系数 $\alpha_{ij}$ 的计算方法：

$\begin{aligned} e_{ij} &= \mathrm{LeakyReLU}\left(a^\top [W\mathbf{h}_i\;||\;W\mathbf{h}_j]\right) \\ \alpha_{ij} &= \mathrm{softmax}(e_{ij})=\frac{\exp{(e_{ij})}}{\sum_{k\in N(i)}\exp{(e_{ik})}} \end{aligned}$

式中，我们先对两个节点特征进行仿射变换，然后拼接在一起，再和权重向量 $a$ 作内积，通过非线性激活函数 $\rm LeakyReLU$ 得到评分函数，利用 $\rm softmax$ 进行归一化得到权重系数。整个过程可以用下图描述：

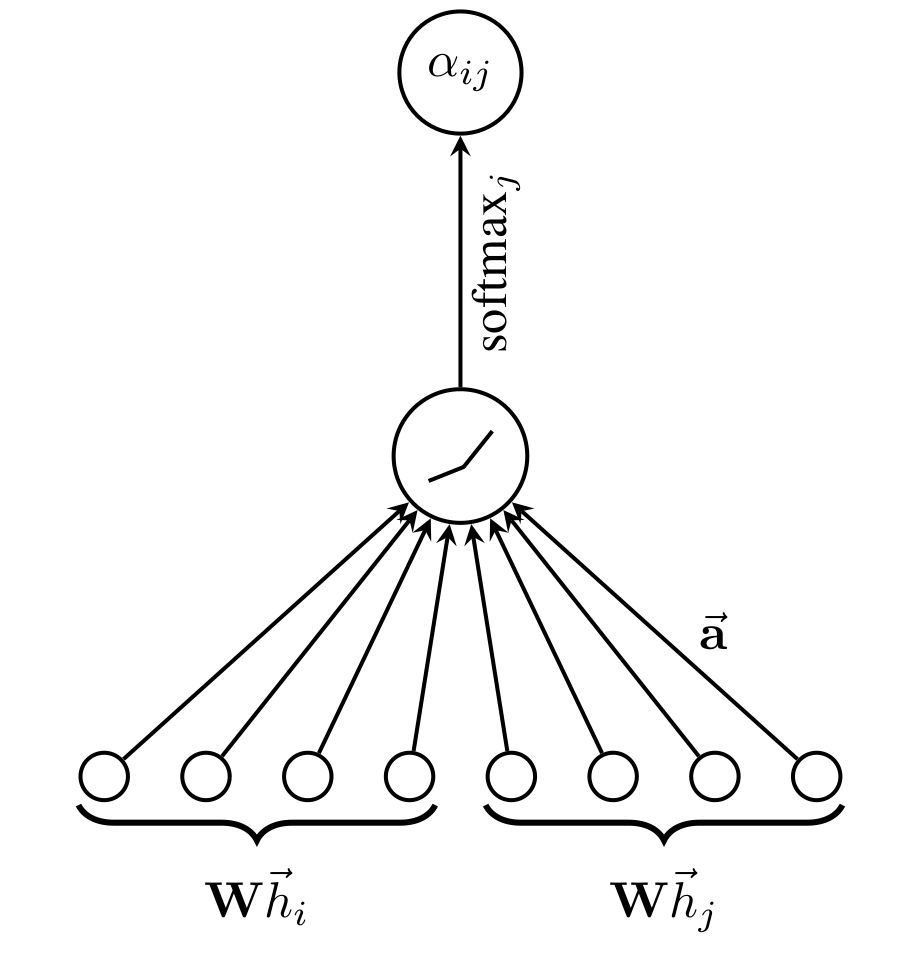
最终，我们得到节点 $i$ 的嵌入表示更新公式为：

$\mathbf{h}_i' = \sigma\left(\sum_{j\in N(i)}\alpha_{ij}W\mathbf{h}_j\right)$

当 $K\gt1$ 时，即采用了多头注意力机制之后，多头得到的嵌入表示可以利用拼接或求平均值的方式得到。下图展示的是节点 1 在 $K=3$ 层的图注意力网络下，得到的更新嵌入。

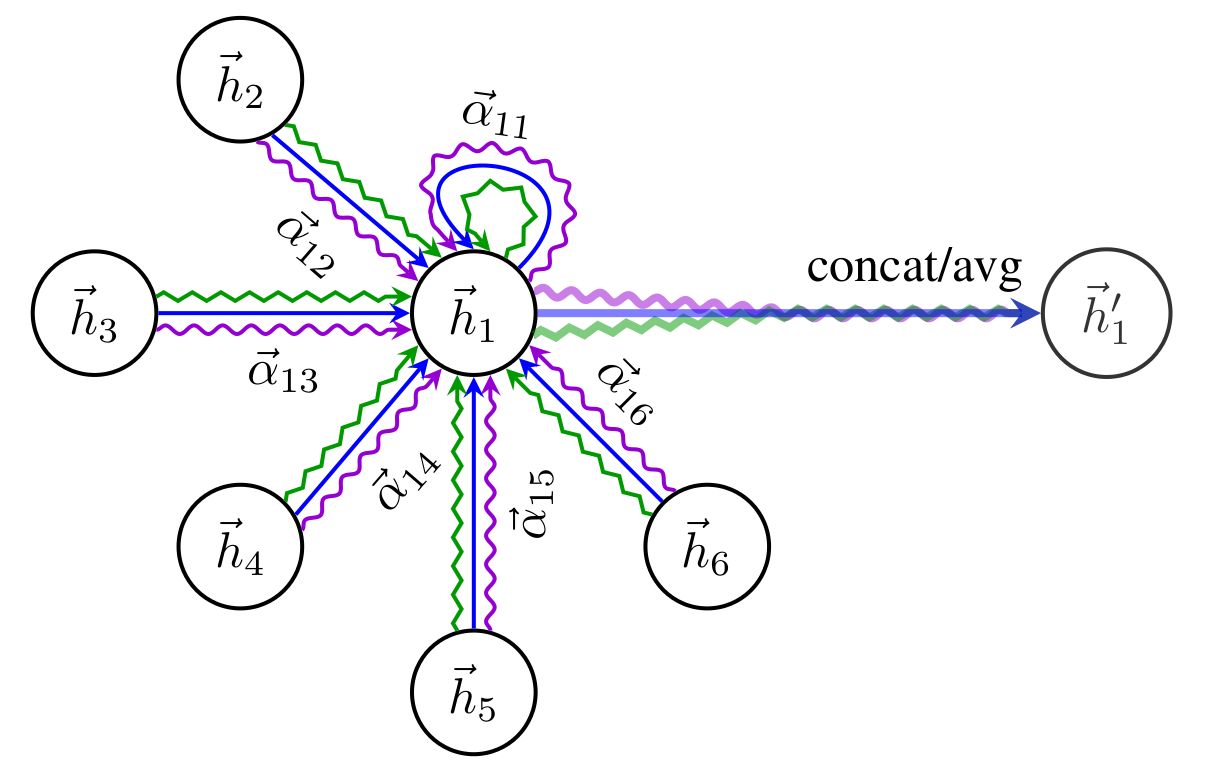
多头图注意力机制

GAT如何解决问题

针对前面提出的 GCNs 的问题，GAT是如何攻破的呢？这里做出简要的说明。

GAT因为只学习注意力机制的线性变换权重，而并不依靠训练集的图的结构。所以图中再次产生新的结点时，只要知道边连关系就能直接前向传播计算出结果。
GAT只依靠边连关系，对有向图来说很友好，而GCN因为拉普拉斯矩阵的对称性，所以不能直接处理有向图；
同(1)，就算给出新的图，只要知道边连关系（且保证特征维度与训练集相同）就能直接前向传播计算结果。

循环图神经网络

图神经网络的另一种趋势是在前向传播过程中使用 GRU 或 LSTM 等 RNN 门控机制，以弥补基础 GNN 模型的不足，并且能够提高长距离信息传播的有效性。

本站循环神经网络总结性文章：

序列浅学：循环神经网络

https://qslie.top/posts/db061ab9

Note：因为循环图神经网络流派是为了弥补基础GNN模型而分支下去的，与前述我们大量探讨的图卷积网络不同，循环图网络还在想办法解决基于巴拿赫不动点定理而产生的设定停止参数、迭代更新问题。

GGNN | 门控图网络

2016年 门控图神经网络(Gated Graph Neural Network, GGNN) 被 Yujia Li 等人提出。GGNN 将隐状态的迭代看作是一个长度为 $T$ 的序列输入的隐状态更新过程。从而利用 RNN 中的门控循环单元来进行更新。

GGNN 的更新公式如下：

$\mathbf{h}^{(t+1)}_v=\text{GRU}\left(\mathbf{h}^{(t)}_v,\sum_{𝑢∈N(𝑣)} \mathbf{W}_{edge}𝐡_u^{(t)}\right)$

具体来说，把第 $t$ 次迭代得到的隐状态（目标节点 $v$ 的嵌入表示） ${\bf h}_v^{(t)}$ 看作是GRU中在时间步 $t$ 时的输入，把 $v$ 所有相邻节点的嵌入表示进行加权求和，以作为GRU中“过去所有数据的隐状态”。

Graph-LSTM

2017年，吸收了基于树结构的LSTM模型：Child-Sum Tree-LSTM、N-ary Tree-LSTM，Nanyun Peng 等人进一步提出了 Graph-LSTM，为不同的边标签使用不同的可学习的遗忘门权重、输出门权重和输入门权重。

前言